Centrifugaalpomp Lexicon
Opvoerhoogteverliezen zijn een gevolg van wandwrijving in alle soorten pijpleidingen en van plaatselijke weerstand tegen stroming, bijvoorbeeld in kleppen en appendages (zie ook Drukverlies).
Aanbevolen stroomsnelheden
- Voor koud water:
Aanzuigleiding 0.7-1,5 m/s
Losleiding 1,0-2,0 m/s - Voor warm water:
Aanzuigleiding 0,5-1,0 m/s
Losleiding 1,5-3,5 m/s
De vergelijking voor het drukverlies van een stroming in een recht stuk leiding met cirkelvormige doorsnede luidt:
λ Leidingwrijvingsfactor
L Leidinglengte in m
d Buisbinnendiameter in m
v Stroomsnelheid in een doorsnede in m/s
(= 4 Q / π d2 met Q in m3/s)
g Versnelling door de zwaartekracht in m/s2
zie Fig. 1 en 4 Opvoerhoogteverlies
De leidingwrijvingsfactor werd experimenteel vastgesteld. Deze is slechts afhankelijk van de stromingstoestand van de behandelde vloeistof en van de relatieve ruwheid (d/k) van de pijpen waardoor de vloeistof stroomt. Voor niet-cirkelvormige buisdoorsneden geldt de equivalente diameter in vloeistofmechanische termen (d):
A Doorsnede in m2
U Omtrek van de natgemaakte doorsnede in m
(het vrije oppervlak van een open kanaal wordt buiten beschouwing gelaten)
De stromingstoestand wordt bepaald door het Reynoldsgetal (Re) volgens de affiniteitswetten. Voor ronde pijpen geldt:
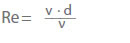
v Stroomsnelheid in een dwarsdoorsnede in m/s
(= 4 Q / π d2 met Q in m3/s)
ν Kinematische viscositeit in m2/s
(voor water bij 20 °C: 1.00 – 10 – 6 m2/s)
d Buisbinnendiameter in m
Zie fig. 4 Opvoerhoogteverlies
Voor hydraulisch gladde leidingen zoals glad getrokken metalen of kunststof leidingen (b.v. PE of PVC), of in het geval van laminaire stroming, kan de buiswrijvingsfactor (λ) worden berekend. Bij laminaire stroming in een pijp met een Reynoldsgetal kleiner dan 2320 is de pijpwrijvingsfactor onafhankelijk van de ruwheid:
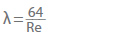
In geval van turbulente stroming, of bij een Reynoldsgetal hoger dan 2320, kan de pijpwrijvingsfactor in hydraulisch gladde pijpen worden weergegeven met een empirische vergelijking volgens Eck (omdat de afwijkingen kleiner zijn dan 1 % als het Reynoldsgetal lager is dan 108).
De buiswrijvingsfactor (λ) hangt ook af van een andere dimensieloze parameter, namelijk van de relatieve ruwheid van het binnenoppervlak van de buis (d/k). Beide moeten in dezelfde eenheid (b.v. mm) worden opgegeven.
Zie fig. 1 Opvoerhoogteverlies
(k) is de gemiddelde absolute ruwheid van het binnenoppervlak van de buis waarvoor benaderende waarden beschikbaar zijn, afhankelijk van het materiaal en het fabricageprocédé. Zie fig. 2 Opvoerhoogteverlies
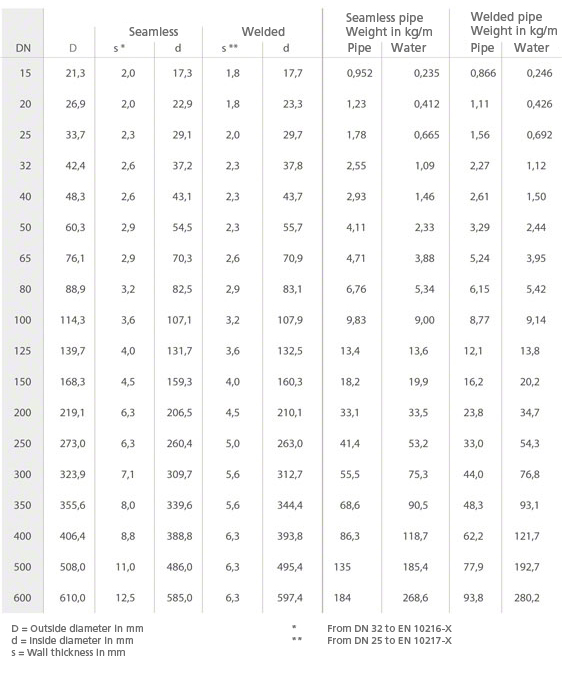Fig. 2 Opvoerhoogteverlies: Schattingen van gemiddelde piek-dalhoogten k (absolute ruwheid) van pijpen
Boven de grenscurve is de wrijvingsfactor (λ) van de pijp uitsluitend afhankelijk van de relatieve ruwheid (d/k) van de pijp. Zie fig. 1 Opvoerhoogteverlies
De volgende empirische vergelijking van Moody kan voor dit gebied worden gebruikt:
Voor praktisch gebruik wordt het opvoerhoogteverlies (HL) per 100 m rechte stalen pijp in het diagram weergegeven als functie van het debiet (Q) en de binnendiameter van de pijp (d).
Zie fig. 3 Opvoerhoogteverlies
De waarden zijn alleen geldig voor koud, schoon water of voor vloeistoffen met dezelfde kinematische viscositeit, voor volledig gevulde pijpen en voor een absolute ruwheid van het binnenoppervlak van de pijp van k = 0.05 mm.
Afmetingen, gewichten, watervulling voor nieuwe naadloze of in de lengterichting gelaste stalen buizen
Zie bijlage, Opvoerhoogteverlies, fig. 4
Het effect van een grotere oppervlakteruwheid k zal in het onderstaande worden aangetoond voor een veelgebruikte reeks parameterbereiken (nominale diameter DN = 50 tot 300, stroomsnelheid v = 0,8 tot 3,0 m/s). Zie Fig. 3 Opvoerhoogteverlies
Het lichtblauwe gebied komt overeen met het eveneens gemarkeerde gebied voor een absolute gemiddelde ruwheid van k = 0,05 mm.
Zie Fig. 1 Opvoerhoogteverlies
Voor een ruwheid verhoogd met een factor 6 (licht geïncrusteerde oude stalen pijp met k = 0,30 = 300 μm (0.30 mm) zijn de buiswrijvingsfactoren (en de bijbehorende proportionele opvoerhoogteverliezen) in het donkerblauwe gebied slechts 25 – 60 % hoger dan voorheen.
Zie fig. 1 Opvoerhoogteverlies
Bij rioolbuizen moet rekening worden gehouden met de verhoogde ruwheid als gevolg van vervuiling. Voor buizen die aan extreme corrosie onderhevig zijn, kan het werkelijke drukverlies alleen proefondervindelijk worden vastgesteld. Afwijkingen van de nominale diameter veranderen het drukverlies aanzienlijk, aangezien de binnendiameter van de buis in de vergelijking tot de vijfde macht meespeelt.
Een vermindering van de binnendiameter met 5 % leidt bijvoorbeeld tot een toename van het drukverlies met maar liefst 30 %. Het is daarom van belang dat de binnendiameter bij de berekeningen niet zonder meer wordt vervangen door de nominale diameter.
De drukverliezen in kunststofbuizen of glad getrokken metalen buizen zijn zeer gering dankzij de gladde buisoppervlakken. De vastgestelde opvoerhoogteverliezen gelden voor water bij 10 °C. Bij andere temperaturen moet het verlies voor kunststofleidingen worden vermenigvuldigd met een gespecificeerde temperatuurcorrectiefactor om rekening te houden met hun grotere thermische uitzetting. Voor rioolwater of ander onbehandeld water moet rekening worden gehouden met een extra drukverlies van 20-30 % in verband met mogelijke afzettingen.
Hoogteverliezen voor kunststof- en gladgetrokken metalen buizen
Zie bijlage, Hoogteverlies, fig. 5
Hoogteverliezen in afsluiters en hulpstukken
Hoogteverlies (HL) in afsluiters en hulpstukken wordt gegeven door:
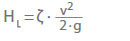
ζ Verliescoëfficiënt
Zie Fig. 6 t/m 12 Verlies
v Stroomsnelheid in een karakteristieke dwarsdoorsnede A
(b.v. bij het mondstuk) in m/s
g Versnelling ten gevolge van de zwaartekracht 9,81 m/s2
Fig. 6 Verlies van de hoofddoorsnede: Schematische weergave van klepontwerpen
Fig. 11 Opvoerhoogteverlies: Invloed op de verliescoëfficiënt ζ van het afronden van de binnen- en buitenzijde van ellebogen in vierkante kanalen
Fig. 12 Opvoerhoogteverlies: Verliescoëfficiënten ζ voor vlinder-, bol- en schuifafsluiters afhankelijk van de openingsgraad
De verliezen die zijn toe te schrijven aan het rechttrekken van de stromingsstoringen over een buislengte gelijk aan 12 x DN stroomafwaarts van de afsluiter, zijn opgenomen in de verliescoëfficiënten overeenkomstig de VDI/VDE 2173-richtlijn. De waarden gelden voor kleppen die een gestage aanstroom hebben, volledig geopend zijn en met koud water worden bediend. Afhankelijk van de in- en uitstroomomstandigheden, de klepmodellen en de ontwikkelingsdoelstellingen (d.w.z. goedkope of energiebesparende kleppen), kunnen de verlieswaarden sterk variëren. Zie bijlage, Opvoerhoogteverlies, fig. 7
Vaak wordt bij de berekening van het drukverlies voor water in kleppen de kv-waarde gebruikt in plaats van de verliescoëfficiënt (ζ):
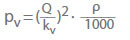
De kv-waarde is het debiet in m3/h dat zou resulteren uit een drukval pv = 1 bar door de klep voor koud water. Zij beschrijft de correlatie tussen het drukverlies (pL) in bar en het debiet (Q) in m3/h. Omrekening naar doorstroomcoëfficiënt ζ voor koud water:
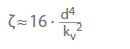
d Referentie (nominale) diameter van de klep in cm
Voor de berekening van de opvoerhoogteverliezen in fittingen, aftakkingen en verloopstukken is een andere aanpak nodig. Zie fig. 9 en 10 Verlies
Fig. 9 Verlies: Verliescoëfficiënten ζ voor fittingen 
Fig. 10 Verliescoëfficiënten ζ voor adapters: Verliescoëfficiënten ζ voor adapters
Voor alle fittingen moet onderscheid worden gemaakt tussen twee vormen van drukverlies:
- Ireversibel drukverlies (drukverlaging)
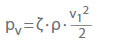
pv Drukverlies in Pa
ζ Verliescoëfficiënt
ρ Dichtheid in kg/m3
v Stroomsnelheid in een doorsnede in m/s
pvdoorsnede in m/s
- Omkeerbare drukveranderingen van de wrijvingsloze stroming volgens de vergelijking van Bernoulli
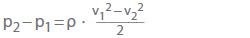
Voor versnelde stromingen, zoals verkleiningen van de pijpdiameter, (p2 – p1) is altijd negatief; voor vertraagde stromingen, zoals pijpuitzettingen, is het altijd positief. Bij de berekening van de netto drukverandering als de rekenkundige som van pL en (p2 – p1) moeten de onomkeerbare drukverliezen altijd worden afgetrokken.
Invloed van zeer visceuze vloeistoffen op de systeemkarakteristiek
Omdat de wetten van de vloeistofdynamica hun geldigheid behouden voor alle Newtonse vloeistoffen, zijn de vergelijkingen en diagrammen voor de berekening van de buiswrijvingsfactoren en verliescoëfficiënten voor afsluiters ook toepasbaar op visceuze vloeistoffen met een hogere viscositeit dan water.
Bij de berekening van het Reynoldsgetal Re = v – d / ν , moet men eenvoudig de kinematische viscositeit van de viskeuze vloeistoffen νz vervangen door de waterviscositeit νz.
Dit levert een lager Re-getal op en, volgens fig. 1 Opvoerhoogteverlies, een grotere buiswrijvingscoëfficiënt λz (Opmerking: de invloed van de wandruwheid kan nu vaak worden verwaarloosd vanwege de grotere grenslaagdikte in de stroming).
Alle drukverliezen in leidingen en kleppen die voor water zijn berekend, moeten worden geëxtrapoleerd met behulp van de verhouding λz/λw.
Figuur 13 Opvoerhoogteverlies is ook geschikt voor algemeen praktisch gebruik: de buiswrijvingsfactor λz kan snel worden bepaald als functie van het debiet Q, de binnendiameter van de leiding d en de kinematische viscositeit νz. Er moet echter rekening mee worden gehouden dat de coëfficiënt λw in dit diagram alleen geldt voor hydraulisch gladde leidingen (dus niet voor ruwe leidingen)! De bijbehorende λw kan worden gebruikt om de verhouding λz/λw te berekenen.
Aangezien de statische component van de systeemkarakteristiek Hsys , zie fig. 1 Systeemkarakteristiek en fig. 2 Opvoerhoogte, niet wordt beïnvloed door viscositeit, kan de dynamische component van de systeemkarakteristiek voor water worden hertekend als een steilere parabool voor een viskeuze vloeistof.
Invloed van niet-Newtoniaanse vloeistoffen op de systeemkarakteristiek
Aangezien de stromingskrommen geen rechte lijnen van constante lineaire viscositeit zijn, is de berekening van de opvoerhoogteverliezen zeer omslachtig. In dit geval is de verliesberekening gebaseerd op ervaring met bepaalde vloeistoffen.