Úvod do pravděpodobnosti: Články a videa s řešeními!

admin 0 Comments Articles

Úvod do pravděpodobnosti: Články a videa s řešeními!

Házení kostkou, hledání parkovacího místa, výhra v kartách; To jsou jen některé situace, kdy můžete chtít zjistit pravděpodobnost, že se nějaká událost stane. Pokud chcete vědět, jak zjistit pravděpodobnost, musíte nejprve zjistit, o jakou otázku se jedná. Například způsob, jak zjistit pravděpodobnost, že se nějaká událost stane, se liší od zjištění pravděpodobnosti, že si členové skupiny vyberou stejnou věc.

Některé pravděpodobnosti lze určit snadno, například zjistit pravděpodobnost hodu kostkou nebo výběru z balíčku karet.

Snadno se také identifikují otázky, které zahrnují binomickou větu. V těchto typech pokusů jsou jedinými možnými výsledky události „úspěch“ nebo „neúspěch“: jako ano/ne, hlava/ocas nebo černá/bílá.

Další typy otázek, se kterými se můžete setkat, se týkají lidí, například:

• Výběr osoby ze skupiny nebo komise.
• Možnost, že si skupina vybere stejnou věc.

Události

Chcete zjistit pravděpodobnost, že nastane jednoduchá událost? Třeba že bude pršet nebo že najdete místo na parkování v centru města? Viz:
Pravděpodobnost, že nastane jednoduchá událost.
Na druhou stranu, pokud chcete přesný opak, viz:
Jak zjistit pravděpodobnost, že událost nenastane.

Je vaše otázka o tom, že jedna událost nastane vzhledem k jiné události? Například pravděpodobnost nalezení parkovacího místa vzhledem k tomu, že je den hry, nebo nalezení určité populární hračky na černý pátek? Pokud ano, podívejte se na:

• Šance, že nastane nějaká událost vzhledem k jiné události.
• Dvě události, které nastanou společně.

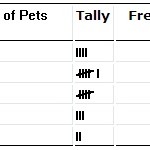
Tabulka rozdělení četností.

Rozdělení četností

Máte rozdělení četností, se kterým můžete pracovat? Nebo jste schopni vytvořit tabulku rozdělení četností s danými daty? Například máte x položek s určitými znaky. Pravděpodobnostní rozdělení četností.

Úvod do pravděpodobnosti: návodné články a videa.

1. Permutace a kombinace: Jak řešit úlohy
2. Problémy s pravděpodobností:
3. Pravděpodobnost a a b.
4. Pravidlo celkové pravděpodobnosti.
5. Problémy s Bayesovou větou:
6. Přednostní pravděpodobnost (včetně neinformativní a konjugované).
7. Jak vytvořit rozdělení pravděpodobnosti z dat.
8. Jak zjistit pravděpodobnost výběru osoby ze skupiny nebo komise.
9. Jak zjistit pravděpodobnost, že se událost NEstane.
10. Rozdělení četností pravděpodobnosti.
11. Jak zjistit pravděpodobnost, že se stane jednoduchá událost.
12. Náhodná událost:
13. Jak zjistit pravděpodobnost, že členové skupiny zvolí stejnou věc.
14. Jak zjistit pravděpodobnost, že dvě závislé události nastanou společně.
15. Jak zjistit pravděpodobnost výskytu události vzhledem k jiné události.
16. Jak použít strom pravděpodobnosti (rozhodovací strom) k výpočtu šancí.
17. Jak zjistit pravděpodobnost vytažení karty z balíčku.
18. Jak zjistit, zda je něco vzájemně se vylučující událostí.
19. Jak rozlišit závislé a nezávislé události.
20. Pravděpodobnost:
21. Jak nakreslit Vennův diagram.
22. Jak vytvořit Eulerův diagram.
23. 5 vybrat 3: jak řešit kombinace.
24. Jak použít základní princip počítání.
25. Jak najít očekávanou hodnotu diskrétní náhodné veličiny.

Úvod do pravděpodobnosti: Definice

• Axiomatická pravděpodobnost.
• Benfordův zákon
• Co je to binomický experiment?
• Základní sazby a omyl o základní sazbě
• Brierovo skóre
• Kolektivně vyčerpávající
• Co jsou kombinace
• Komplementární události.
• Podmíněné očekávání
• Co je podmíněná relativní četnost?
• Počitatelná aditivita
• Prázdná množina
• Epistemická pravděpodobnost
• Prostory událostí.
• Co je experimentální pravděpodobnost
• Spojitá rozdělení pravděpodobnosti.
• Omezující rozdělení.
• Odhad maximální pravděpodobnosti
• Vlastnost bez paměti.
• Metoda Monte Carlo.
• Monty Hallův problém
• Co je to vzájemně exkluzivní událost.
• Co je to vzájemně inkluzivní událost?
• Vzájemně nezávislé a párově nezávislé.
• Co je to pravidlo násobení?
• Nashova rovnováha
• Prázdná množina
• Normální pravděpodobnostní úlohy k procvičení.
• Co je normální pravděpodobnostní graf
• Objektivní pravděpodobnost
• Co je poměr šancí
• Prediktivní analýza
• Co je tabulka rozdělení pravděpodobnosti?
• Míra pravděpodobnosti
• Co je pravděpodobnostní prostor?
• Pravděpodobnostní vektory
• Co jsou to výběrové prostory?
• Stochastické modely.
• Co je subjektivní pravděpodobnost?
• Co je teoretická pravděpodobnost?
• Co je urnový model?

Kalkulačky.

• Online kalkulačka permutací a kombinací.

Pravděpodobnostní vzorce / Pravidla pravděpodobnosti

Jednou z nejnepříjemnějších věcí, které studenti nemají rádi na vzorcích, je jejich nedostatek v pravděpodobnosti a statistice. Existuje několik základních vzorců, včetně některých povinných zápisů:

Rozsah pravděpodobnosti
0 ≤ P(A) ≤ 1
Ten říká, že pravděpodobnost události je někde mezi nulou a 100 % (v desetinném čísle je to 0 a 1). Toto pravidlo si budete chtít zapamatovat při sčítání nebo násobení pravděpodobností událostí. Pokud je vaše odpověď vyšší než 100 %, je to vodítko, že jste možná udělali něco špatně.

Pravidlo komplementárních událostí
P(AC) + P(A) = 1
Komplementární události nastávají, když existují pouze dva výsledky, například při házení mincí. Házení kostkou, abyste zjistili, zda vám padne šestka, je také komplementární; jediné dva výsledky jsou, že padne šestka (šance 1/6), nebo že šestka nepadne (šance 5/6). Obě pravděpodobnosti musí dát dohromady 1.
Tento vzorec můžete také vidět zapsaný takto:
p(A) + p(A‘) = 1
což lze algebraicky přeformulovat takto:
p(A‘) = 1 – p(A).
Všechny tři vzorce jsou ekvivalentní: jakou terminologii (A‘ nebo Ac) použijete, záleží na autorovi učebnice a učiteli. Osobně dávám přednost A‘, kterému říkám „ne A“. Pravděpodobnost „ne A“ je podle mě srozumitelnější než „doplněk“ (buď se událost stane, nebo se nestane).

Pravidlo sčítání
P(A∪B) = P(A) + P(B) – P(A∩B)
kde ∪ je sjednocení a ∩ je průnik.
Co to říká (anglicky!) je, že pravděpodobnost, že nastane událost A NEBO událost B (nebo obě současně), je:

• Pravděpodobnost, že nastane událost A sama o sobě,
• Přičteme-li pravděpodobnost, že nastane událost B sama o sobě,
• Přičteme-li pravděpodobnost, že nastanou obě události současně.

Pokud máme vzájemně se vylučující události, pak P(A∩B) nemůže nastat (události nemohou nastat společně), takže vzorec se stává:
P(A∪B) = P(A)+P(B)- 0 = P(A)+P(B)

Disjunktní události
Události A a B jsou disjunktní, jestliže:
P(A∩B) = 0
To je jen jiný způsob, jak říci, že události se navzájem vylučují. Nemohou nastat současně.

Související formule je P((A∪B)c) nebo ekvivalentně ((A∪B)‘). V angličtině to znamená „not the union“. Vyřešíte to tak, že zjistíte, jaká je unie, a výsledek odečtete od 1 (protože pravděpodobnost, že události nastanou nebo nenastanou, musí dát dohromady 1).

Podmíněná pravděpodobnost
P(A|B) = P(A∩B) / P(B)
Symbol „|“ znamená „za předpokladu, že“. Jinými slovy, pravděpodobnost, že nastane událost B za předpokladu, že nastane událost A. Příklady použití vzorce najdete na stránce: Podmíněná pravděpodobnost.

Bayesův vzorec
P(A|B) = P(B|A) – P(A) / P(B)
Bayesova věta je způsob, jak zjistit podmíněnou pravděpodobnost, i když je poněkud nuancovanější. Stručně řečeno, udává skutečnou pravděpodobnost události vzhledem k informacím o testech. Například jaká je pravděpodobnost, že máte rakovinu, pokud je váš lékařský test pozitivní (odpověď = mnohem nižší, než si myslíte). Některé příklady viz: Příklady Bayesovy věty a Posteriorní rozdělení / Posteriorní pravděpodobnosti.

Nezávislé události
Události A a B jsou nezávislé, jestliže jedna z nich neovlivňuje pravděpodobnost druhé. O událostech se také říká, že jsou nezávislé, jestliže platí následující rovnice:
P(A∩B) = P(A) – P(B).
Tato rovnice je odvozena z pravidla násobení, které říká, že P(A∩B) = P(A) * P(B|A). Protože víme, že P(B|A) = P(B) pro nezávislé události, můžeme nahradit P(B|A) za P(B), čímž získáme vzorec.

Několik poznámek k pravidlům pravděpodobnosti

Statistika je o náhodě a odhadu, nikoli o absolutních hodnotách a „správné odpovědi“. Stačí se podívat na jakýkoli Gallupův průzkum – málokdy jsou si jistí více než 90 %, že mají „správnou odpověď“. Existují techniky, které můžete použít k určení pravděpodobnosti (například vynásobení dvou pravděpodobností dohromady nebo jejich sečtení). Kromě snad binomické distribuční tabulky a výše uvedených vzorců (které se v reálném životě příliš nepoužívají) však ve skutečnosti neexistují žádné pravděpodobnostní vzorce, které byste mohli snadno použít. Musíte se vrátit ke staré známé věci ze základní školy, k logice (pamatujete si ji… byla tam těsně předtím, než z vás začali standardizovaně zkoušet logiku).

Tři pravidla pravděpodobnostních vzorců:

1. Neexistují žádná pravidla (no, jen velmi málo, kromě těch výše uvedených).
2. Používejte logiku, ne rovnice.
3. Existuje mnoho, mnoho různých způsobů, jak se dostat k odpovědi – žádný z nich ve skutečnosti nepoužívá vzorce.

Tady je otázka, která mi dnes ráno přišla do schránky a která se zabývá pravděpodobností:

„Kdybyste se snažili nasbírat 6 baseballových kartiček, které jsou v balíčcích se sýrem, za předpokladu, že jsou rozděleny rovnoměrně, kolik balíčků sýra byste očekávali, že koupíte, než budete mít všech 6 kartiček?“

Krokem 1 k vyřešení tohoto problému je uvědomit si, že odpověď nemůžete hledat v tabulce. Abyste ji vyřešili, musíte přemýšlet jako dítě.

Karta č. 1:Zase je vám 8 let a jdete do obchodu s penězi, za které si můžete koupit jeden sáček sýrových chlebíčků. Doufáš, že nasbíráš všech 5 baseballových karet, ale zatím žádnou nemáš. Jaká je pravděpodobnost, že si sáček koupíte a získáte kartu, kterou chcete?“

Odpověď je samozřejmě 100%. Když si koupíš první sáček, máš 100% šanci, že v něm bude karta, kterou chceš.

Karta č. 2: Teď to bude trochu složitější. Vrátíš se do obchodu, abys získal kartu#2. Protože jste však již získali kartu č. 1, Mickeyho Mantla. Už ho nechceš, ale je tu 1/5 šance, že ho dostaneš (a tedy 4/5 šance, že ho nedostaneš). Problémem poměru se stává otázka, kolik sáčků sýrových chlebíčků si budete muset koupit, abyste získali kartu č. 2. Můžete si to spočítat v hlavě, ale pokud to chcete modelovat matematicky, musíte sestavit rovnici. Pokud vám jeden sáček sýrových chlebíčků dává 80% šanci, že získáte požadovanou kartu, kolik sáčků musíte koupit, abyste získali 100% šanci?

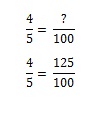
Pro získání 100% šance byste museli koupit 1,25 sáčku.

Karta#3:Šance začíná být těžší. Máte 60% šanci získat třetí baseballovou kartu a k získání této třetí karty byste museli koupit 1,667 pytle.

Card# 4:Šance začínají být poněkud neutěšené. Máte 40% šanci, že získáte čtvrtou baseballovou kartu, a budete si muset koupit 2,5 pytle, abyste získali tuto třetí kartu.

Card# 5:Šance jsou proti vám. Máte 20% šanci, že získáte poslední kartu, a budete si muset koupit 5 sáčků, abyste získali tuto třetí kartu.

Takže celkový počet sáčků, které budete muset koupit, se rovná:
1 + 1,25 + 1,667 + 2,5 + 5
Ale počkejte! (A tady přichází na řadu trocha logiky). Nemůžete jít do obchodu a koupit 1,25 sáčku sýrových oblátek, takže budete muset zaokrouhlovat nahoru. Z rovnice se stane:
1 + 2 + 2 + 3 + 5 = 13 sáčků.

Jedna důležitá poznámka k vzorcům: pamatujte, že nic není absolutní. Jsem si dostatečně jistý, že pokud byste si koupili 13 sáčků sýrových chlebíčků a předpokládali rovnoměrné rozložení karet, že byste získali všech 5 karet. Ale… pravděpodobnost je o náhodě a může se stát, že budete mít prostě smůlu a dostanete 10krát za sebou stejnou kartu (vzpomínám si, že se mi to stalo jako dítěti). Ale mohlo by existovat i jiné vysvětlení vaší „smůly“, a to, že společnosti chtějí, abyste si koupili co nejvíce sáčků, takže se budou snažit, aby šance pracovala v jejich prospěch. I když jsou karty rozděleny rovnoměrně, společnost by mohla poslat sáčky s kartami č. 1, 2 a 3 do jednoho obchodu (čímž by vás přiměla nasbírat více než polovinu karet) a č. 4 a 5 do jiného obchodu.

Jaké další způsoby vás napadají, jak by výrobci mohli zvrátit šance ve svůj prospěch?

Pravděpodobnost, že si skupina vybere stejnou věc

Pravděpodobnostní otázky lze rozdělit na různé typy. Když máte zjistit pravděpodobnost, že si skupina vybere stejnou věc, uvažujete o jednání náhodných členů skupiny (může být tak malá jako výbor nebo tak velká jako populace USA).
Tyto pravděpodobnostní otázky vám dávají skupinu a žádají vás, abyste vypočítali pravděpodobnost výskytu události pro určitý počet náhodných členů této skupiny.

Probability of a Group Choosing the Same Thing : Steps

Vzorový problém: Na knižním veletrhu je 200 lidí. Z nich si 159 koupí alespoň jednu knihu. Pokud provedete průzkum u 5 náhodných lidí vycházejících ze dveří, jaká je pravděpodobnost, že si všichni koupí alespoň jednu knihu?

Jaká je pravděpodobnost, že si skupina koupí alespoň jednu knihu?

Krok 1: Převeďte údaje v otázce na zlomek. Například větu „159 lidí z 200“ lze převést na:

Krok 2: Vynásobte zlomek sám sebou. Postup opakujte pro libovolný počet náhodně vybraných položek (tj. lidí). V našem příkladu máme 5 dotazovaných osob, takže chceme:

159/200 x 159/200 x 159/200 x 159/200 x 159/200 x 159/200 = 0,3176
Takto zjistíme pravděpodobnost, že si skupina vybere stejnou věc!

Tip: Možná bude jednodušší převést zlomek před vynásobením na desetinné číslo. V tomto případě 159/200 = 0,795.

Pro více nápovědy a tipů ke statistice se podívejte na náš kanál YouTube! Máme videa pro nejčastější problémy, se kterými se pravděpodobně setkáte. Plus videa pro použití Excelu ve statistice > vše od tvorby základních sloupcových grafů až po řešení složitých problémů analýzy dat.

——————————————————————————

Potřebujete pomoci s domácím úkolem nebo testovou otázkou? S Chegg Study můžete získat řešení svých otázek krok za krokem od odborníka v oboru. Prvních 30 minut s lektorem Chegg je zdarma!