Definice vlnové funkce
Fundamentální částice, jako jsou elektrony, lze popsat jako částice nebo vlny.
Elektrony lze popsat pomocí vlnové funkce, jejímž symbolem je řecké písmeno psi, Ψ nebo ψ.

Vlnová funkce Ψ je matematický výraz.Nese zásadní informaci o elektronu, s nímž je spojena:z vlnové funkce získáme energii elektronu, jeho úhlový moment hybnosti a orientaci orbitalu ve tvaru kvantových čísel n, l a ml.
Vlnová funkce může mít kladné nebo záporné znaménko.znaménko je důležité při výpočtech.je také důležité, když se vlnové funkce dvou nebo více atomů spojí a vytvoří molekulu.
Vlnové funkce se stejným znaménkem (vlny ve fázi) budou interferovat konstruktivně, což vede k možnosti vazby. vlnové funkce s nestejným znaménkem (vlny mimo fázi) budou interferovat destruktivně.
V roce 1926 Erwin Schrödinger odvodil vlnovou funkci pro nejjednodušší ze všech atomů, vodík. řešení Schrödingerovy rovnice umožňuje vědcům určit vlnové funkce pro elektrony v atomech a molekulách.
Schrödingerova rovnice je rovnicí kvantové mechaniky: vypočtené vlnové funkce mají diskrétní, povolené hodnoty pro elektrony vázané v atomech a molekulách; všechny ostatní hodnoty jsou zakázané.
Kromě významu Ψ má v chemii obrovský význam také její čtverec Ψ2.
Ψ2 je hustota pravděpodobnosti.Říká nám, kde se elektron v prostoru kolem jádra s největší pravděpodobností nachází.
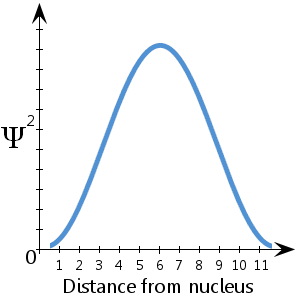
Například na (fiktivním) schematickém diagramu, který je zde vynesen a znázorňuje Ψ2 v závislosti na vzdálenosti od jádra, vidíme, že elektron se s největší pravděpodobností nachází v rozmezí asi 5-7 jednotek od jádra. vidíme také, že je mizivá pravděpodobnost, že se elektron bude nacházet u jádra nebo více než asi 11½ jednotky od jádra.
Existuje stoprocentní pravděpodobnost, že se elektron někde nachází – jinými slovy pravděpodobnost 1.
Ψ lze přesně vypočítat pouze pro atomy s jedním elektronem, tedy H, He+, Li2+, Be3+, B4+, C5+ atd. v matematickém jazyce říkáme, že analytické řešení pro Ψ je možné pouze pro jednoelektronové systémy. jednoelektronové systémy se často označují jako hydrogenní – což znamená „jako vodík.“
Pro všechny ostatní atomy, ionty a molekuly není analytické řešení pro Ψ možné; k jeho výpočtu jsou nutné aproximační metody.
Ψ2 a vodíkové orbitaly
Při vykreslení hustoty pravděpodobnosti vodíku (tj.Ψ2) pro různá kvantová čísla nám umožňuje představit si prostor se středem v jádře, který elektrony zaujímají. různá rozložení Ψ2 jsou elektronové orbitaly vodíku.Orbital, který je skutečně obsazen, je určen množstvím energie, kterou elektron má.
Příklady orbitalů vodíku
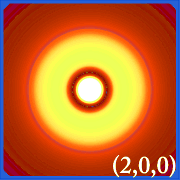
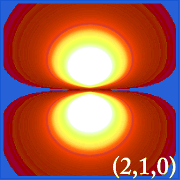

.








