Entropie – pilíř termodynamiky i teorie informace
Entropie je vágní, ale mocný pojem, který tvoří páteř mnoha klíčových myšlenek termodynamiky a teorie informace. Poprvé byl identifikován fyzikálními vědci v 19. století a působil jako vůdčí princip mnoha převratných technologií průmyslové revoluce. Tento termín však také pomohl nastartovat informační věk, když se objevil v přelomovém díle matematika Clauda Shannona A Mathematical Theory of Communication. Jak tedy může být jeden termín zodpovědný za dva přelomové objevy, které od sebe dělí zhruba jedno století, v příbuzných, a přesto odlišných oborech?
Nejprve začněme tím, jak je entropie interpretována ve fyzikálních vědách. První termodynamický zákon stanoví, že v každém uzavřeném systému nelze energii ani vytvořit, ani zničit. Druhý zákon, známý také jako zákon entropie, stanoví, že v otevřeném systému energie vždy proudí od vyšší koncentrace k nižší, aby bylo dosaženo termodynamické rovnováhy. Co to znamená v praxi? Znamená to, že váš hrnek kávy nakonec vychladne a led v nápoji časem roztaje, nebo že nástroj umístěný do ohně se zahřeje, protože energie z plamene přechází na molekuly železa, ale po jeho odstranění se ochladí, protože energie se rozdělí do nového okolního prostředí.

Sám pojem entropie označuje stav neuspořádanosti v daném systému. Energie v koncentrované a využitelné formě je považována za uspořádanou, zatímco energie v rozptýlené a nedostupné formě je považována za neuspořádanou.
Entropie se pohybuje pouze jedním směrem – k rovnováze – pokud na ni nepůsobí síla mimo systém, a i tehdy se vnějším silám, jako jsou biologické systémy, daří proces entropie zvrátit pouze dočasně a nakonec ustoupí (prostřednictvím smrti). Každá rostlina nebo živočich je složitý energetický systém, který přežívá díky vyrovnávání entropického procesu a shromažďování dostupné, uspořádané energie z prostředí a následnému vylučování odpadu zbaveného živin. Průchodnost energie v živém systému však nakonec degraduje jeho fyzickou strukturu, což způsobí, že se organismus rozpadne a zemře (doufejme, že po splnění svého konečného cíle – rozmnožování). Tělo energie, které již není živé, se rozloží a rozptýlí do okolního prostředí – a nastane termodynamická rovnováha.
Teoreticky se entropie zastaví na svém vytrvalém pochodu teprve tehdy, až přivodí tepelnou smrt vesmíru – konečný konečný stav, kdy neexistuje žádná volná energie. Vše na zemi i ve vesmíru se nakonec rozpíná, exploduje, odumře a rovnoměrně rozdělí volnou energii v tom, co je ve skutečnosti největším uzavřeným systémem ze všech: ve vesmíru. Entropie je tak univerzálním zákonem podobným gravitaci, neboť působí jak v nejmenším, tak v největším měřítku biofyziky.
Ekonomika jsou organismy, ne pračky
Entropie se vztahuje i na ekonomiku. Proces entropie uvnitř organismu tím, že získává dostupnou energii z okolního prostředí a přeměňuje ji na neuspořádanou energii, platí i pro skupiny organismů. Společnosti přijímají zdroje energie s nízkou entropií ve dvou formách: zásoby a toky. Zásoby zahrnují minerály vzácných zemin, fosilní paliva a další pozemská ložiska vytvořená složitými, dlouhodobými zemskými procesy v průběhu tisíciletí. Toky pocházejí z tzv. obnovitelných zdrojů, jako jsou vítr, voda a sluneční energie, mezi něž patří také biomasa (jako nepřímé rozšíření sluneční energie). Vzhledem k povaze jednotlivých zdrojů jsou zásoby omezené co do množství, zatímco toky jsou omezené co do rychlosti i množství. Civilizace, stejně jako organismy, mají svůj metabolismus. Zpracovávají energii.

Průmyslová revoluce poprvé přesunula primární energetický vstup ekonomiky z toků na pozemské zásoby. Pluhy poháněné koňmi a větrné plachty, dvě formy práce závislé na tocích, byly nahrazeny mechanizovaným zemědělstvím a plavidly poháněnými parou, které jsou závislé na fosilních palivech. Využili jsme spící sluneční energii fosilizovanou po miliony let, abychom osvobodili civilizaci od omezení biologických zemských toků a vytvořili závratný růst populace a HDP.
Přes nepopiratelné ekonomické a materiální výhody této změny měla vedlejší účinek v podobě urychlení procesu entropie a zvýšení nepořádku v klimatickém systému. Přestože celkové množství energie zůstává ekonomickým procesem nezměněno (s výjimkou sluneční energie), těžba nerostných surovin a spotřeba fosilních paliv nutná pro výrobní proces charakterizuje kvalitativní změnu, která posouvá energii od řádu k neuspořádanosti. Entropie tak tvoří základ nedostatku, protože lidé nemohou přesunout energii opačným směrem, tedy ze stavu neuspořádanosti do uspořádanosti; bez entropie by bylo fyzikálně možné přeměnit atmosférický CO2 zpět na hroudu uhlí, stejně jako by bylo možné zachytit a rekonfigurovat částice gumy ztracené při degradaci pneumatiky na vozovce.

Nakonec naše ekonomika využívá věci a energii. Přestože peníze, naše reprezentace hodnoty, krouží ekonomikou neomezeně dlouho, fyzické statky, které reprezentují, podléhají zákonu entropie. Současný ekonomický systém je jako organismus, který roste donekonečna. Naše srdce pumpuje krev a udržuje nás při životě, ale tato síla časem opotřebovává naše buňky. Stárneme a degradujeme.
Jak se tedy entropie vztahuje k datové vědě?
Když jsme se podívali na to, jak se entropie vztahuje k energii, podívejme se, jak se vztahuje ke komunikaci a informační teorii. Myslím, že tento úryvek z biografie Clauda Shannona A Mind at Play od Jimmyho Soniho a Roba Goodmana je skvělým anekdotickým příběhem o vzniku entropie:
Shannon oslovil velkého muže se svou myšlenkou informace jako vyřešené neurčitosti – která se stane jádrem jeho práce – a s neskromnou otázkou. Jak by měl tuto věc nazvat? Von Neumann odpověděl okamžitě: „Řekněme, že informace snižuje ‚entropii‘. Za prvé je to dobré, solidní fyzikální slovo. A co je důležitější,“ pokračoval, „nikdo neví, co entropie ve skutečnosti je, takže v debatě budete mít vždycky výhodu.“

Než se pustíme do Shannonovy definice entropie, možná nám pomůže rozebrat jeho definici informace. Základní myšlenkou Shannonovy teorie je, že informační hodnota sdělované zprávy závisí na tom, do jaké míry je obsah zprávy překvapivý. Skvělým příkladem v praxi je využití četnosti písmen v jazyce. Z pravděpodobnostního hlediska, pokud je výskyt písmene jednou událostí, pak se nejpravděpodobnější výsledek každé dané události řídí tímto rozdělením pravděpodobnosti:
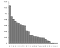
Čím více je písmen, tím menší je nejistota ve sdělení. Záleží však také na vzácnosti písmene. Která z následujících zpráv má například větší informační náboj, 1 nebo 2?“
_AT
Varianta „1“ obsahuje dvě písmena s poměrně vysokou pravděpodobností, kdy doplněním chybějícího písmene můžete vyluštit nejrůznější slova: „Bat“, „Cat“, „Hat“, „Fat“, „Sat“ atd. Možnost 2 obsahuje poměrně nepolapitelné písmeno „H“, které má několik zbývajících možností slov jako „Klobouk“ nebo „Hit“, ale ne tolik jako možnost 1. Varianta 2 tedy sděluje více informací, protože ve větší míře snižuje neurčitost.
Jestliže je tedy informace řešenou neurčitostí, musí být entropie neurčitostí, kterou je třeba řešit. Vzácnost události neboli její „překvapivost“ určuje její informační obsah (pokud jste někdy hráli Scrabble, věděli byste, jak omezené by byly možnosti, kdybychom si vylosovali písmeno „Q“). Pokaždé, když sdělíme nějakou informaci, celková entropie, neuspořádanost, neurčitost nebo jak to chcete nazvat, se úměrně tomu snižuje nebo klesá. Jaké je tedy toto poměrné množství?
Shannon vypočítal, že míra informační entropie spojená s každou možnou hodnotou dat je záporný logaritmus funkce hmotnosti pravděpodobnosti pro danou hodnotu:
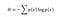
Entropie měří očekávané množství informace zprostředkované identifikací výsledku náhodné události, kde možné výsledky jsou funkcí pravděpodobnosti. Z toho vyplývá, že hod kostkou má vyšší entropii než hod mincí, protože každý výsledek hodu kostkou (⅙) má menší pravděpodobnost než padnutí hlavy nebo oře (½). Grafický pohled na tento vztah pomáhá:

Při sdělení výsledku hlava víme, že orel nenastal.
Ve strojovém učení se matematická interpretace entropie používá k výpočtu metriky informačního zisku u mnoha algoritmů. Například rozhodovací stromy vybírají jeden z mnoha různých atributů, známých také jako rysy nebo nezávislé proměnné, aby opakovaně rozdělily vzorky do podmnožin. Při každém rozdělení algoritmus vybere jeden atribut, podle kterého vzorek rozdělí, a pokračuje v tom, dokud nejsou všechny podmnožiny čisté, nebo jinými slovy, každý jednotlivý vzorek v podmnožině má stejnou klasifikační nebo cílovou hodnotu.
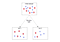
K měření čistoty podmnožiny vzorků potřebuje algoritmus kvantitativní měřítko, aby mohl objektivně vybrat, podle kterého znaku se má v každém daném uzlu rozdělit. K tomu slouží entropie. V každém kroku algoritmus vypočítá, který atribut vykáže nejvyšší informační zisk, a poté rozhodne o rozdělení. Vypočítá také očekávaný pokles neurčitosti před rozdělením a po něm; pokud se sníží, rozdělení se zachová a algoritmus přejde k dalšímu kroku. Pokud se nesnížila, dosáhl čistoty a odpočívá. Tímto způsobem je zodpovědný jak za výběr funkce, která se má rozdělit, tak za zastavení procesu.
Existuje souvislost mezi termodynamikou a teorií informace?
Entropie neúprosně proudí rozhodovacím stromem, stejně jako neúprosně proudí šálkem kávy do vzduchu. V energetice kráčí k termodynamické rovnováze, v teorii informace kráčí k čistotě.
V jádru se energetická interpretace entropie a interpretace entropie v teorii informace sbíhají ve stejném bodě – v základních fyzikálních zákonech. Komunikace vyžaduje energii a využívání energie vyžaduje komunikaci. Podle Shannona poskytuje hodnota entropie informace absolutní limit pro nejkratší možnou průměrnou délku zprávy, neboli jak moc ji lze komprimovat, aniž by při přenosu došlo ke ztrátě informace. Polovodiče, svítilny a ťukání na pánev v Morseově abecedě vyžaduje lidskou energii a naše komunikace bude vždy usilovat o co nejefektivnější způsob přenosu.
V oblasti energie se snažíme minimalizovat entropii tím, že omezujeme její množství a efektivitu. Naším cílem je najít uspořádané zdroje energie a odolávat vlivu entropie na naše tělo. V komunikaci minimalizujeme entropii tím, že vyhledáváme informace a omezujeme nejistotu. Snížením neuspořádanosti prostřednictvím komunikace můžeme svým způsobem zastavit entropický proces energie; lovec-sběrač může pomocí jazyka komunikovat s jiným člověkem a varovat ho před sežráním lvem, čímž se snižuje nejistota 1. kde se lev nachází (informační entropie) a 2. proces sežrání lvem (energetická entropie). Tento akt komunikace snižuje pravděpodobnostní prostor všech možných událostí a umožňuje nám jednat efektivněji a účinněji. Pochopení podstaty fungování tohoto mocného zákona v digitální a fyzické sféře je klíčem k pochopení souvislostí mezi termodynamikou a informačním věkem.




