Interpretace koeficientů lineární regrese

Interpretace koeficientů lineární regrese

V dnešní době existuje nepřeberné množství algoritmů strojového učení, které můžeme vyzkoušet, abychom našli ten nejvhodnější pro náš konkrétní problém. Některé algoritmy mají jasnou interpretaci, jiné fungují jako černá skříňka a k odvození některých interpretací můžeme použít přístupy jako LIME nebo SHAP.

V tomto článku bych se rád zaměřil na interpretaci koeficientů nejzákladnějšího regresního modelu, tedy lineární regrese, včetně situací, kdy došlo k transformaci závislých/nezávislých proměnných (v tomto případě mluvím o logaritmické transformaci).

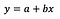
Předpokládám, že čtenář je s lineární regresí obeznámen (pokud ne, existuje spousta dobrých článků a příspěvků na Médiu), proto se zaměřím pouze na interpretaci koeficientů.

Základní vzorec pro lineární regresi je vidět výše (záměrně jsem vynechal rezidua, aby to bylo jednoduché a výstižné). Ve vzorci y označuje závislou proměnnou a x je nezávislá proměnná. Pro zjednodušení předpokládejme, že se jedná o jednorozměrnou regresi, ale principy samozřejmě platí i pro vícerozměrný případ.

Pro představu řekněme, že po dosazení modelu dostaneme:

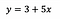
Intercept (a)

Rozdělím interpretaci interceptu na dva případy:

• x je spojité a centrované (odečtením průměru x od každého pozorování se průměr transformovaného x stane 0) – průměr y je 3, když x je rovno výběrovému průměru
• x je spojité, ale není centrovaná – průměr y je 3, když x = 0
• x je kategoriální – průměr y je 3, když x = 0 (tentokrát označuje kategorii, více o tom níže)

Koeficient (b)

• x je spojitá proměnná

Interpretace: Zvýšení x o jednotku má za následek zvýšení průměrného y o 5 jednotek, všechny ostatní proměnné zůstávají konstantní.

• x je kategoriální proměnná

Toto vyžaduje trochu více vysvětlení. Řekněme, že x popisuje pohlaví a může nabývat hodnot („muž“, „žena“). Nyní ji převedeme na dummy proměnnou, která nabývá hodnot 0 pro muže a 1 pro ženy.

Interpretace: průměrné y je vyšší o 5 jednotek u žen než u mužů, všechny ostatní proměnné zůstávají konstantní.

Model na úrovni logaritmu

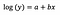
Typicky používáme transformaci logaritmu, abychom vytáhli odlehlá data z pozitivně zkresleného rozdělení blíže k většině dat, aby byla proměnná normálně rozdělena. V případě lineární regrese je jednou z dalších výhod použití logaritmické transformace interpretovatelnost.

Stejně jako dříve řekněme, že níže uvedený vzorec představuje koeficienty fitovaného modelu.

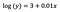
Intercept (a)

Interpretace je podobná jako v případě vanilky (úrovně), avšak pro interpretaci musíme vzít exponent interceptu exp(3) = 20,09. V tomto případě je třeba vzít exponent interceptu. Rozdíl je v tom, že tato hodnota znamená geometrický průměr y (na rozdíl od aritmetického průměru v případě modelu na úrovni).

Koeficient (b)

Principy jsou opět podobné jako u modelu na úrovni, pokud jde o interpretaci kategoriálních/číselných proměnných. Analogicky k interceptu musíme vzít exponent koeficientu: exp(b) = exp(0,01) = 1,01. V tomto případě je třeba vzít exponent koeficientu. To znamená, že jednotkový nárůst x způsobí 1% nárůst průměrného (geometrického) y, přičemž všechny ostatní proměnné zůstávají konstantní.

Zde stojí za zmínku dvě věci:

• Při interpretaci koeficientů takového modelu existuje pravidlo. Pokud abs(b) < 0,15, lze zcela bezpečně říci, že při b = 0,1 budeme pozorovat 10% nárůst y při jednotkové změně x. U koeficientů s větší absolutní hodnotou se doporučuje vypočítat exponent.
• Pokud se jedná o proměnné v rozsahu (například procenta), je pro interpretaci výhodnější proměnnou nejprve vynásobit 100 a pak model dosadit. Takto je interpretace intuitivnější, protože proměnnou zvýšíme o 1 procentní bod místo o 100 procentních bodů (z 0 na 1 ihned).

level-log model

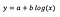
Předpokládejme, že po dosazení modelu dostaneme:

Interpretace interceptu je stejná jako v případě modelu na úrovni.

Pro koeficient b – 1% zvýšení x vede k přibližnému zvýšení průměrného y o b/100 (v tomto případě 0,05), všechny ostatní proměnné zůstávají konstantní. Abychom získali přesnou hodnotu, museli bychom vzít b × log(1,01), což v tomto případě dává 0,0498.

log-log model

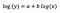
Předpokládejme, že po dosazení modelu dostaneme:

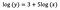
Znovu se zaměřím na interpretaci b. Zvýšení x o 1 % vede k 5% zvýšení průměrného (geometrického) y, všechny ostatní proměnné zůstávají konstantní. Abychom získali přesnou částku, musíme vzít

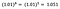
což je ~5,1 %.

Závěry

Doufám, že vám tento článek poskytl přehled o tom, jak interpretovat koeficienty lineární regrese, včetně případů, kdy byly některé proměnné logaritmicky transformovány. Jako vždy uvítáme jakoukoli konstruktivní zpětnou vazbu. Můžete se na mě obrátit na Twitteru nebo v komentářích.