Povrch válce – vysvětlení a příklady
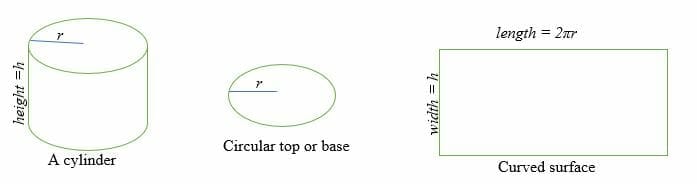
Než se vrhneme na téma povrchu válce, zopakujme si, co je to válec. V geometrii je válec trojrozměrný útvar se dvěma navzájem rovnoběžnými kruhovými podstavami a zakřiveným povrchem.
Jak zjistit povrch válce?
Povrch válce je součet dvou rovnoběžných a shodných kruhových ploch a plochy zakřiveného povrchu.
Tento článek pojednává o tom, jak zjistit celkový povrch a povrch příčné plochy válce.
Pro výpočet povrchu válce je třeba zjistit plochu podstavy (B) a plochu zakřivené plochy (CSA). Povrch neboli celkový povrch válce se tedy rovná součtu plochy podstavy krát dvě a plochy zakřiveného povrchu.
Zakřivený povrch válce se rovná obdélníku, jehož délka je 2πr a šířka je h.
Kde r = poloměr kruhové plochy a h = výška válce.
Plocha zakřiveného povrchu = Plocha obdélníku =l x w = πdh
Plocha podstavy, B = Plocha kružnice = πr2
Vzorec pro plochu válce
Vzorec pro celkovou plochu válce je dán takto:
Celkový povrch válce = 2πr2 + 2πrh
TSA = 2πr2 + 2πrh
Kde 2πr2 je plocha horní a dolní kruhové plochy a 2πrh je plocha zakřivené plochy.
Vezmeme-li 2πr jako společný činitel z RHS, dostaneme;
TSA = 2πr (h + r) ……………………………………. (Vzorec pro povrch válce)
Řešme příkladové úlohy týkající se povrchu válce.
Příklad 1
Najděte celkový povrch válce, jehož poloměr je 5 cm a výška je 7 cm.
Řešení
Podle vzorce,
TSA = 2πr (h + r)
= 2 x 3. Jaký je celkový povrch válce?14 x 5(7 + 5)
= 31,4 x 12
= 376,8 cm2
Příklad 2
Najděte poloměr válce, jehož celkový povrch je 2136,56 čtverečních stop a výška je 3 stopy.
Řešení
Dáno:
TSA = 2136.56 čtverečních stop
Výška, h = 3 stopy
Ale, TSA = 2πr (h + r)
2136,56 =2 x 3,14 x r (3 + r)
2136,56 = 6.28r (3 + r)
Podle distributivní vlastnosti násobení na RHS máme,
2136,56 = 18,84r + 6,28r2
Dělíme každý člen 6,28
340.22 = 3r + r2
r2 + 3r – 340,22 = 0 ……… (kvadratická rovnice)
Řešením rovnice pomocí kvadratického vzorce dostaneme,
r = 17
Poloměr válce je tedy 17 stop.
Příklad 3
Náklad na natření válcové nádoby je 0,04 $ za cm2. Zjistěte náklady na natření 20 nádob o poloměru 50 cm a výšce 80 cm.
Řešení
Vypočítejte celkovou plochu 20 nádob.
TSA = 2πr (h + r)
= 2 x 3. Jaké jsou náklady na natření 20 nádob?14 x 50 (80 + 50)
= 314 x 130
= 40820 cm2
Celková plocha 20 kontejnerů = 40 820 cm2 x 20
= 816 400 cm2
Náklady na nátěr = 816 400 cm2 x 0 USD.04 za cm2
= $32 656,
Náklad na natření 20 kontejnerů je tedy $32 656,
Příklad 4
Zjistěte výšku válce, je-li jeho celkový povrch 2552 in2 a poloměr 14 in.
Řešení
Dáno:
TSA = 2552 in2
Poloměr, r = 14 in.
Ale TSA = 2πr (h + r)
2552 = 2×3.14 x 14 (14 + h)
2552 = 87,92(14 + h)
Dělením obou stran číslem 87,92 získáme,
29.026 = 14 + h
Na obou stranách odečteme 14.
h = 15
Výška válce je tedy 15 in.
Boční plocha válce
Jak již bylo uvedeno, plocha zakřiveného povrchu válce se označuje jako boční plocha. Zjednodušeně řečeno, boční povrch válce je plocha válce bez plochy podstavy a dna (kruhové plochy).
Vzorec udává boční povrch válce;
LSA = 2πrh
Příklad 5
Zjistěte boční povrch válce, jehož průměr je 56 cm a výška 20 cm.
Řešení
Dáno:
Průměr = 56 cm, tedy poloměr, r =56/2 = 28 cm
Výška, h = 20 cm
Podle vzorce,
LSA = 2πrh
= 2 x 3. Jaký je průměr válce?14 x 28 x 20
= 3516,8 cm2.
Příčný povrch válce je tedy 3516,8 cm2.
Příklad 6
Příčný povrch válce je 144 ft2. Je-li poloměr válce 7 ft, najděte jeho výšku.
Řešení
Dáno;
LSA = 144 ft2
Poloměr, r = 7 ft
.




