Vlastnosti čtyřúhelníků – obdélník, čtverec, rovnoběžník, kosodélník, lichoběžník
V euklidovské geometrii je čtyřúhelník čtyřstranný 2D obrazec, jehož součet vnitřních úhlů je 360°. Slovo čtyřúhelník je odvozeno ze dvou latinských slov „quadri“ a „latus“, což znamená čtyři a strana. Proto je určení vlastností čtyřúhelníků důležité při snaze odlišit je od ostatních mnohoúhelníků.
Jaké jsou tedy vlastnosti čtyřúhelníků? Existují dvě vlastnosti čtyřúhelníků:
- Čtyřúhelník by měl být uzavřený útvar se 4 stranami
- Všechny vnitřní úhly čtyřúhelníku se sčítají do 360°
V tomto článku získáte představu o 5 typech čtyřúhelníků a seznámíte se s vlastnostmi čtyřúhelníků.
To se dočtete v tomto článku:
- Různé typy čtyřúhelníků
- Obdélník
- Vlastnosti obdélníků
- Vzorce pro obdélníky
- Čtverec
- Vlastnosti. čtverce
- Vzorce čtverců
- Rovnoběžník
- Vlastnosti rovnoběžníků
- Vzorce pro rovnoběžníky
- Rovnoběžníky
- Vlastnosti kosočtverce
- Vzorce pro kosočtverec
- Vlastnosti trapézu
- Vzorce pro trapéz
.
Tady je video vysvětlující vlastnosti čtyřúhelníků:
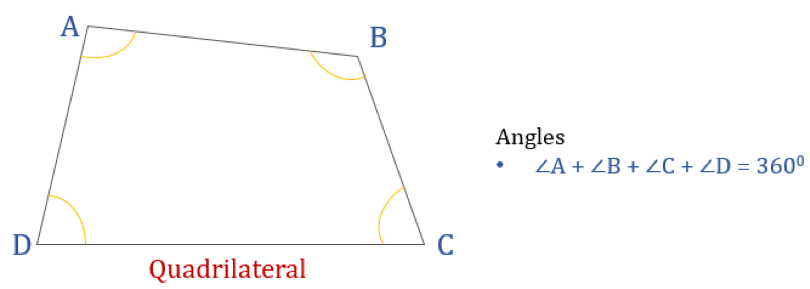
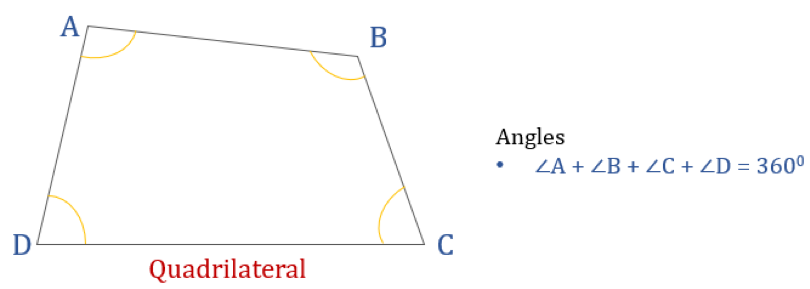
Níže uvedený diagram znázorňuje čtyřúhelník ABCD a součet jeho vnitřních úhlů. Součet všech vnitřních úhlů je 360°.
Tedy ∠A + ∠B + ∠C + ∠D = 360°
Různé typy čtyřúhelníků
Na základě jejich tvaru existuje 5 typů čtyřúhelníků. Těchto 5 čtyřúhelníků je:
- Obdélník
- Čtverec
- Paralelogram
- Rombus
- Trapezium
Probereme si podrobně každý z těchto 5 čtyřúhelníků:
Tady jsou otázky, které vás naučí aplikovat vlastnosti všech 5 čtyřúhelníků, které se dozvíte v tomto článku.
Obdélník
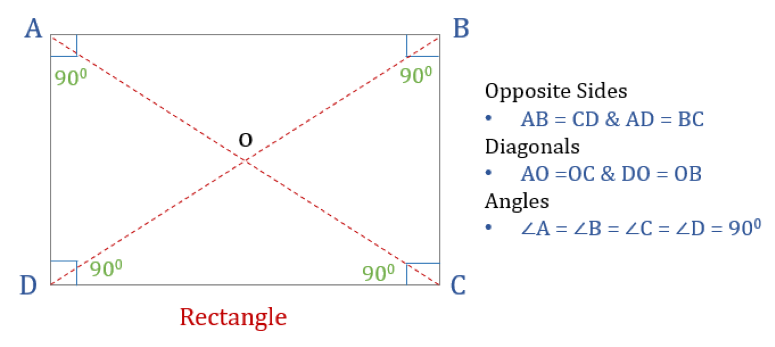
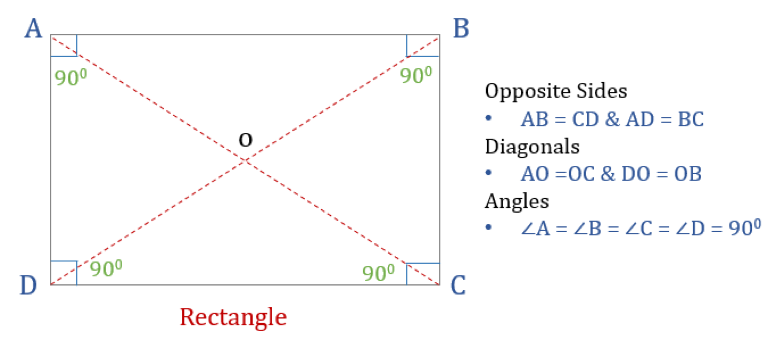
Obdélník je čtyřúhelník se čtyřmi pravými úhly. Všechny úhly v obdélníku jsou tedy stejné (360°/4 = 90°). Kromě toho jsou protilehlé strany obdélníku rovnoběžné a stejné a úhlopříčky se navzájem protínají.
Vlastnosti obdélníků
Obdélník má tři vlastnosti:
- Všechny úhly obdélníku jsou 90°
- Protilehlé strany obdélníku jsou stejné a rovnoběžné
- Příčky obdélníku se navzájem protínají
Velikost a obvod obdélníku
Je-li délka obdélníku L a šířka B, pak,
- Plocha obdélníku = délka × šířka nebo L × B
- Obvod obdélníku = 2 × (L + B)
Tyto procvičovací otázky vám pomohou upevnit si vlastnosti obdélníků
Čtverec
Čtverec je čtyřúhelník se čtyřmi stejnými stranami a úhly. Je to také pravidelný čtyřúhelník, protože jeho strany i úhly jsou stejné. Stejně jako obdélník má čtverec čtyři úhly po 90°. Můžeme si ho také představit jako obdélník, jehož dvě sousední strany jsou stejné.
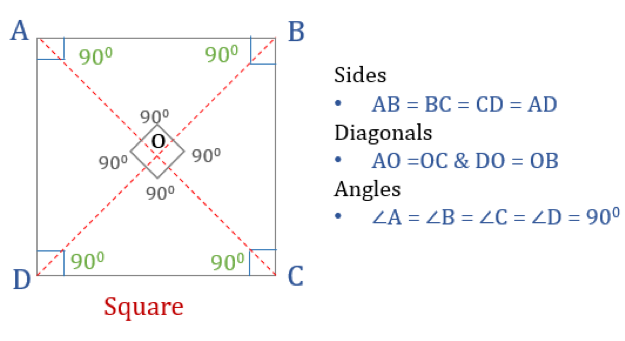
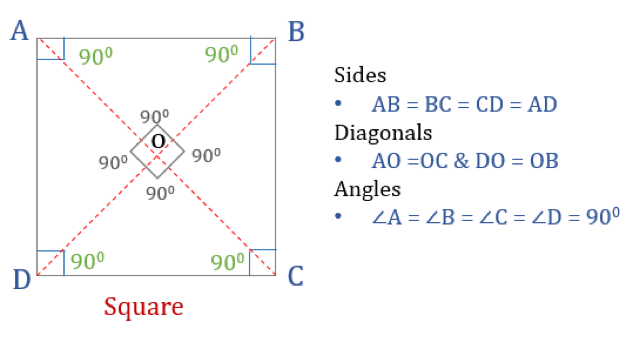
Vlastnosti čtverce
Aby byl čtyřúhelník čtvercem, musí mít určité vlastnosti. Zde jsou tři vlastnosti čtverců:
- Všechny úhly čtverce jsou 90°
- Všechny strany čtverce jsou stejné a navzájem rovnoběžné
- Příčky se navzájem kolmo protínají
Vzorce čtverce – Plocha a obvod čtverce
Je-li strana čtverce „a“, pak,
- Plocha čtverce = a × a = a²
- Obvod čtverce = 2 × (a + a) = 4a
Tyto cvičné otázky vám pomohou upevnit si vlastnosti čtverců
Skórování Q50-51 na testu GMAT vám pomůže získat skóre 700+ GMAT. Proč se nezačít připravovat na zkoušku GMAT s našimi bezplatnými přípravnými zdroji a nezačít svou cestu k získání Q50-51 na zkoušce GMAT. Učte se od Carrie Law, která se za 3 týdny zlepšila z Q35 na Q50.
Paralelogram
Paralelogram, jak už název napovídá, je jednoduchý čtyřúhelník, jehož protilehlé strany jsou rovnoběžné. Má tedy dvě dvojice rovnoběžných stran. Navíc protilehlé úhly v rovnoběžníku jsou stejné a jeho úhlopříčky se navzájem protínají.
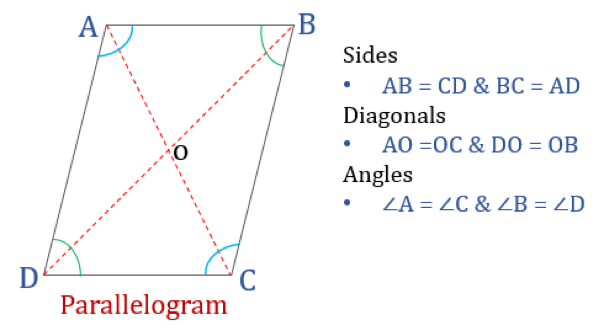
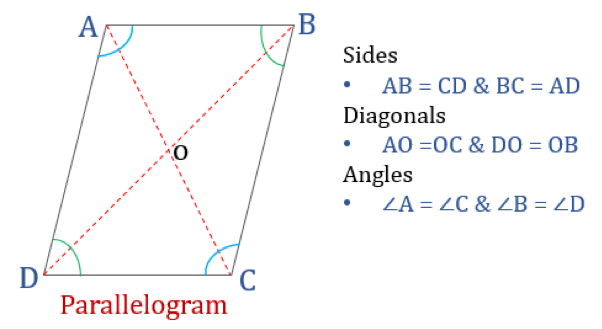
Vlastnosti rovnoběžníku
Čtyřúhelník splňující níže uvedené vlastnosti budeme klasifikovat jako rovnoběžník. Rovnoběžník má čtyři vlastnosti:
- Protilehlé úhly jsou stejné
- Protilehlé strany jsou stejné a rovnoběžné
- Příčky se navzájem protínají
- Součet libovolných dvou sousedních úhlů je 180°
Vzorce pro rovnoběžníky – Plocha a obvod rovnoběžníku
Je-li délka rovnoběžníku „l“, šířka je ‚b‘ a výška je ‚h‘, pak:
- Obvod rovnoběžníku= 2 × (l + b)
- Plocha rovnoběžníku = l × h
Tyto procvičovací otázky vám pomohou upevnit si vlastnosti rovnoběžníku
Rhombus
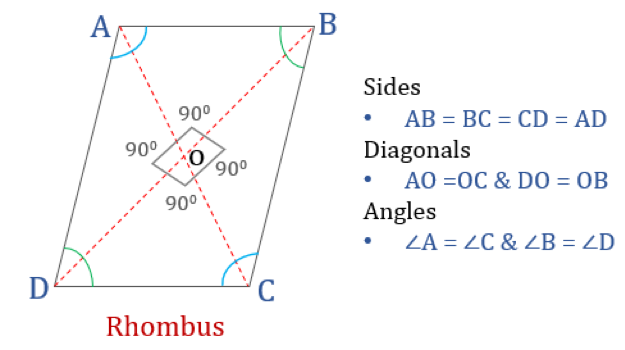
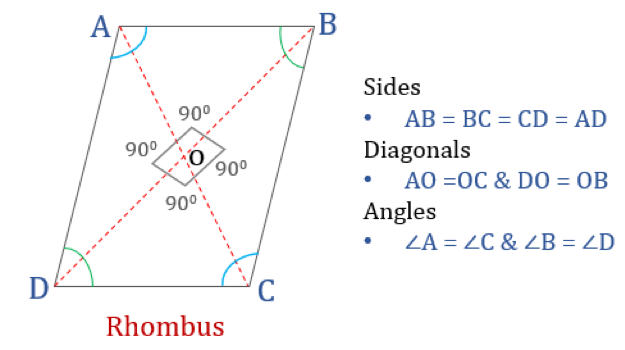
Rhombus je čtyřúhelník, jehož všechny čtyři strany jsou stejně dlouhé a protilehlé strany jsou navzájem rovnoběžné. Úhly však nejsou rovny 90°. Kosočtverec s pravými úhly by se stal čtvercem. Jiný název pro kosočtverec je „diamant“, protože vypadá podobně jako barva diamantu v hracích kartách.
Vlastnosti kosočtverce
Rosmos je čtyřúhelník, který má následující čtyři vlastnosti:
- Protilehlé úhly jsou stejné
- Všechny strany jsou stejné a, protilehlé strany jsou navzájem rovnoběžné
- Příčky se navzájem kolmo protínají
- Součet libovolných dvou sousedních úhlů je 180°
Romby vzorce – Plocha a obvod kosočtverce
Je-li strana kosočtverce a pak, obvod kosočtverce = 4a
Jestliže délky dvou úhlopříček kosočtverce jsou d1 a d2, pak plocha kosočtverce = ½ × d1 × d2
Tyto procvičovací otázky budou vám pomohou upevnit si vlastnosti kosočtverce
Trapezu
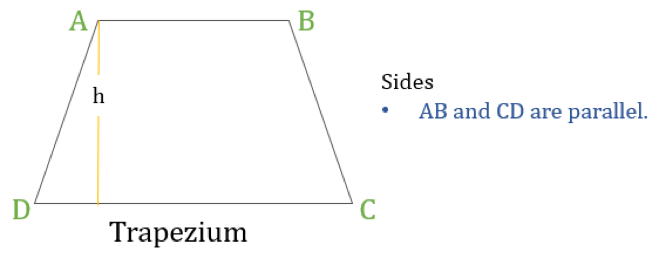
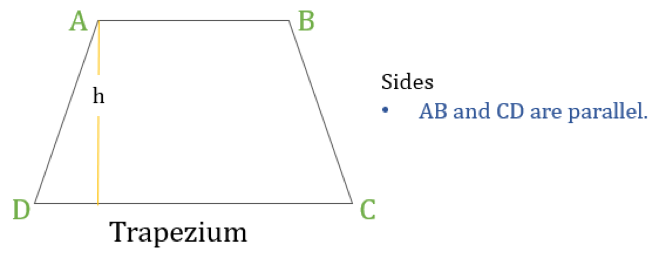
Trapez (v USA nazývaný lichoběžník) je čtyřúhelník, který má pouze jednu dvojici rovnoběžných stran. Rovnoběžné strany se označují jako „základny“ a zbylé dvě strany se nazývají „nohy“ nebo boční strany.
Vlastnosti lichoběžníku
Lachoběžník je čtyřúhelník, který má jednu následující vlastnost:
- Jedna dvojice protilehlých stran je navzájem rovnoběžná
Vzorce pro lichoběžník – Plocha a obvod lichoběžníku
Je-li výška lichoběžníku „h“ (jak je znázorněno na výše uvedeném obrázku), pak:
- Obvod lichoběžníku = součet délek všech stran = AB + BC + CD + DA
- Plocha lichoběžníku = ½ × (součet délek rovnoběžných stran) × h = ½ × (AB + CD) × h
Tyto údaje jsou uvedeny v tabulce. otázky na procvičení vám pomohou upevnit si vlastnosti lichoběžníku
Vlastnosti čtyřúhelníků
V následující tabulce jsou shrnuty všechny vlastnosti čtyřúhelníků, které jsme se dosud naučili:
| Vlastnosti čtyřúhelníků | Obdélník | Čtverec | Paralelogram | Rombus | Trapez | |
| Všechny strany jsou si rovny | ✖ | ✔ | ✖ | ✔ | ✖ | |
| Oprotilehlé Strany jsou stejné | ✔ | ✔ | ✔ | ✔ | ✔ | ✖ |
| Opposite Strany jsou rovnoběžné | ✔ | ✔ | ✔ | ✔ | ✔ | |
| Všechny úhly jsou stejné | ✔ | ✔ | ✖ | ✖ | ✖ | ✖ |
| Protilehlé úhly jsou stejné | ✔ | ✔ | ✔ | ✔ | ✖ | |
| Součet dvou sousedních úhlů je 180 | ✔ | ✔ | ✔ | ✔ | ✖ | |
| Vzájemně se protínají | ✔ | ✔ | ✔ | ✔ | ✖ | |
| Protínají se kolmo | ✖ | ✔ | ✖ | ✔ | ✖ |
Následující obrázek také shrnuje vlastnosti čtyřúhelníků:
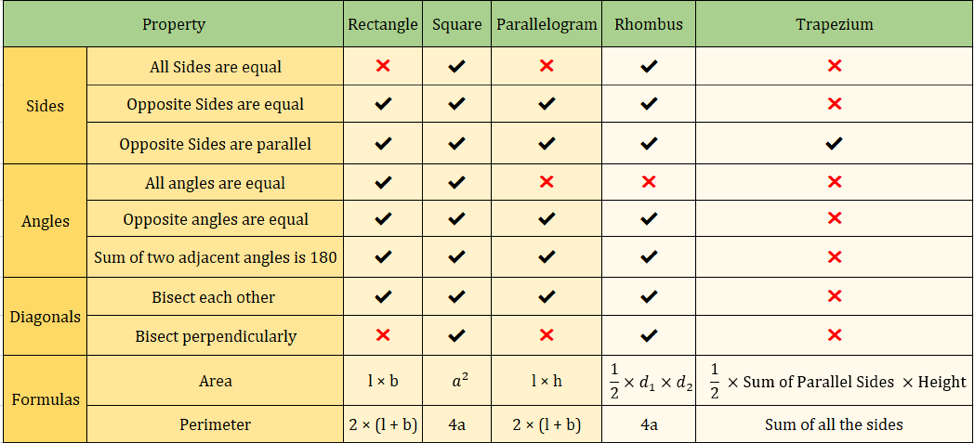
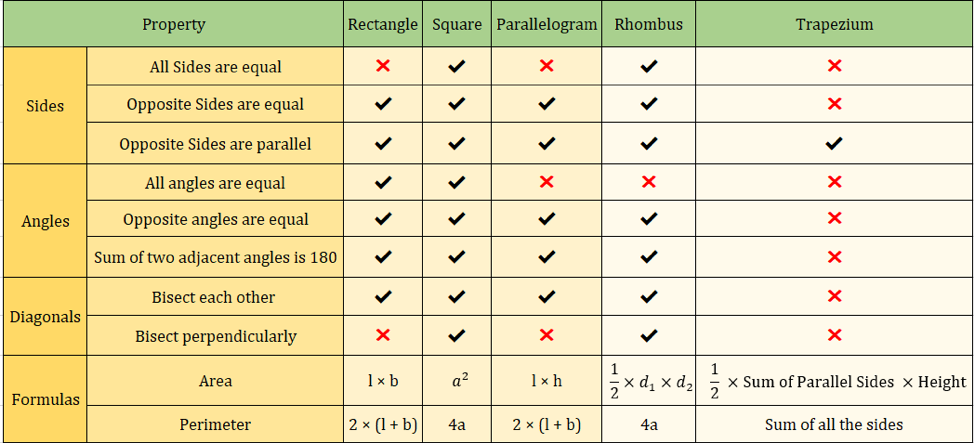
Důležité vzorce pro čtyřúhelníky
Níže uvedená tabulka shrnuje vzorce pro obsah a obvod různých typů čtyřúhelníků:
| Vzorce pro čtyřúhelníky | Obdélník | Čtverec | Paralelogram | Romby | Trapezium |
| Plocha | l × b | a² | l × h | ½ × d1 × d2 | ½ × (součet rovnoběžných stran) × výška |
| Obvod | 2 × (l + b) | 4a | 2 × (l + b) | 4a | Součet všech stran |
Další čtení:
- Vlastnosti kruhu | Vzorce kruhu – plocha a obvod
- Vlastnosti čísel – sudá & lichá | prvočísla | HCF & LCM
- Vlastnosti trojúhelníků – definice | druhy | Klasifikace
- Přímky a úhly – vlastnosti a jejich použití
Otázky na čtyřúhelníky
Procvičíme si použití vlastností čtyřúhelníků na následujících ukázkových otázkách:
Otázka 1
Adam chce postavit plot kolem své obdélníkové zahrady o délce 10 metrů a šířce 15 metrů. Kolik metrů plotu by měl koupit, aby oplotil celou zahradu?
- 20 metrů
- 25 metrů
- 30 metrů
- 40 metrů
- 50 metrů
Řešení
Krok 1: Dáno
- Adam má obdélníkovou zahradu.
- Má délku 10 metrů a šířku 15 metrů.
- Chce kolem ní postavit plot.
Krok 2: Zjistit
- délku potřebnou k postavení plotu kolem celé zahrady.
Krok 3: Přístup a vypracování
Plot lze postavit pouze kolem vnějších stran zahrady.
- Takže celková potřebná délka plotu= Součet délek všech stran zahrady.
- Protože je zahrada obdélníková, součet délek všech stran není nic jiného než obvod zahrady.
- Obvod = 2 × (10 + 15) = 50 metrů
Potřebná délka plotu je tedy 50 metrů.
Správnou odpovědí je tedy možnost E.
Otázka: 2
Steve chce vymalovat jednu stěnu svého pokoje ve tvaru obdélníku. Náklady na vymalování stěny jsou 1,5 dolaru za metr čtvereční. Pokud je stěna dlouhá 25 metrů a široká 18 metrů, jaké jsou celkové náklady na vymalování stěny?
- $ 300
- $ 350
- $ 450
- $ 600
- $ 675
Řešení
Krok 1: Dáno
- Steve chce vymalovat jednu stěnu svého pokoje.
- Stěna je 25 metrů dlouhá a 18 metrů široká.
- Náklad na vymalování stěny je 1,5 dolaru za metr čtvereční.
Krok 2: Zjistit
- Celkové náklady na vymalování stěny.
Krok 3: Přístup a vypracování
- Stěna je vymalována po celé své ploše.
- Zjistíme-li tedy celkovou plochu zdi v metrech čtverečních a vynásobíme-li ji náklady na vymalování 1 metru čtverečního zdi, pak můžeme celkové náklady.
- Plocha zdi = délka × šířka = 25 metrů × 18 metrů = 450 metrů čtverečních
- Celkové náklady na vymalování zdi = 450 × 1 USD.5 = 675 dolarů
Z toho vyplývá, že správnou odpovědí je možnost E.
Doufáme, že jste se do této chvíle seznámili s různými typy čtyřúhelníků, jejich vlastnostmi a vzorci a s tím, jak tyto pojmy použít při řešení otázek týkajících se čtyřúhelníků. Aplikace čtyřúhelníků je důležitá pro řešení otázek z geometrie v testu GMAT. Pokud se chystáte na zkoušku GMAT, můžeme vám pomoci kvalitními studijními materiály, ke kterým získáte přístup zdarma po registraci zde.
Zde je několik dalších článků o matematice:
- Zlepšení přesnosti v matematických otázkách na mnohoúhelníky
- Otázky z geometrie – nejčastější chyby | GMAT Quant Prep
Pokud se chystáte na zkoušku GMAT, můžeme vám poskytnout přístup ke kvalitnímu online obsahu pro přípravu. Jsme nejlépe hodnocenou společností pro přípravu na GMAT na gmatclubu s více než 1950 recenzemi.
Proč si neuděláte bezplatnou zkušební verzi a neposoudíte sami?
V případě jakéhokoli dotazu nám napište na [email protected].
.




