Začáteční algebra
Cíle výuky
- Nakreslit uspořádané dvojice
- Označit součásti souřadnicové roviny
- Vyznačit uspořádané dvojice v souřadnicové rovině
.
- Určit kvadranty v souřadnicové rovině
- Určit čtyři kvadranty souřadnicové roviny
- Podle uspořádané dvojice, určete její kvadrant
Souřadnicová rovina byla vyvinuta před několika staletími (přesněji v roce 1637) a zdokonalena francouzským matematikem René Descartem. Na jeho počest se soustava někdy nazývá kartézský souřadnicový systém. Souřadnicovou rovinu lze použít k vykreslování bodů a grafů přímek. Tento systém nám umožňuje vizuálně popsat algebraické vztahy a také nám pomáhá vytvářet a interpretovat algebraické pojmy.
Složky souřadnicové roviny
Souřadnicovou rovinu jste již pravděpodobně někdy použili. Použili jste například někdy překryvnou mřížku pro zmapování polohy nějakého objektu? (Často se to dělá i u silničních map.)

Tato „mapa“ používá k vyjádření informace o poloze objektu vodorovnou a svislou mřížku. Všimněte si, že písmena A-F jsou uvedena podél horního okraje a čísla 1-6 jsou uvedena podél levého okraje. Obecnou polohu jakéhokoli předmětu na této mapě lze zjistit pomocí písmene a čísla jeho čtverce mřížky. Například položku, která existuje ve čtverci „4F“, najdete tak, že prstem pojedete po vodorovné rovině k písmenu F a pak rovně dolů tak, abyste byli v jedné přímce s číslem 4. Zjistíte, že na tomto místě mapy se nachází modrý disk.
Souřadnicová rovina má podobné prvky jako mřížka zobrazená výše. Skládá se z vodorovné a svislé osy, číselných přímek, které se protínají v pravém úhlu. (Jsou na sebe kolmé.)
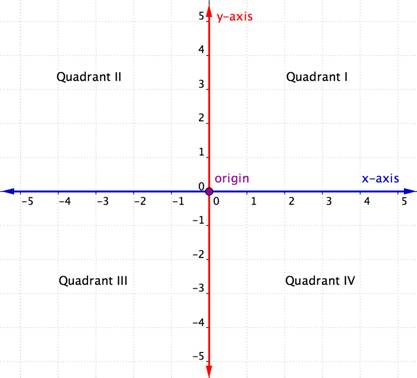
Vodorovná osa v souřadnicové rovině se nazývá osa x. V souřadnicové rovině je vodorovná osa označena jako osa x. V souřadnicové rovině je vodorovná osa označena jako osa x. Svislá osa se nazývá osa y. Bod, ve kterém se obě osy protínají, se nazývá počátek. Počátek je v bodě 0 na ose x a 0 na ose y.
Polohy v rovině souřadnic jsou popsány jako uspořádané dvojice. Uspořádaná dvojice udává polohu bodu vztažením polohy bodu podél osy x (první hodnota uspořádané dvojice) a podél osy y (druhá hodnota uspořádané dvojice).
V uspořádané dvojici, jako je (x, y), se první hodnota nazývá souřadnice x a druhá hodnota je souřadnice y.
V uspořádané dvojici, jako je (x, y), se první hodnota nazývá souřadnice x a druhá hodnota je souřadnice y. Všimněte si, že souřadnice x je uvedena před souřadnicí y. Protože počátek má x-ovou souřadnici 0 a y-ovou souřadnici 0, je jeho uspořádaná dvojice zapsána (0, 0).
Podívejte se na bod níže.

Chcete-li určit polohu tohoto bodu, začněte v počátku (0, 0) a pohybujte se vpravo po ose x, dokud nebudete pod bodem. Podívejte se na popisek na ose x. Označení 4 znamená, že jste od počátku urazili po ose x čtyři jednotky doprava. Jedná se o souřadnici x, první číslo v uspořádané dvojici.
Od čísla 4 na ose x se přesuňte nahoru k bodu a všimněte si čísla, se kterým se zarovnává na ose y. Všimněte si, že na ose y se nachází číslo, se kterým se zarovnává. Číslo 3 znamená, že po opuštění osy x jste urazili 3 jednotky směrem vzhůru ve svislém směru, tedy ve směru osy y. V tomto případě se jedná o 3 jednotky. Toto číslo je y-ová souřadnice, druhé číslo v uspořádané dvojici. Se souřadnicí x 4 a souřadnicí y 3 máte uspořádanou dvojici (4, 3).
Podívejme se na další příklad.
Příklad
Popište zobrazený bod jako uspořádanou dvojici.

Popsat bod zobrazený jako uspořádaná dvojice
Kreslení bodů v souřadnicové rovině
Když už víte, jak používat osy x a y, můžete nakreslit i uspořádanou dvojici. Jen nezapomeňte, že oba postupy začínají v počátku – na začátku! Následující příklad ukazuje, jak vykreslit uspořádanou dvojici (1,3).
Příklad
Vykreslete bod (1, 3).
V předchozím příkladu byly souřadnice x i y kladné. Pokud je jedna (nebo obě) ze souřadnic uspořádané dvojice záporná, budete se muset pohybovat v záporném směru podél jedné nebo obou os. Uvažujte následující příklad, ve kterém jsou obě souřadnice záporné.
Příklad
Vyznačte bod (-4,-2).

Souřadnice x je -4, protože je v uspořádané dvojici na prvním místě. Začněte v počátku a posuňte se po ose x o 4 jednotky záporným směrem (doleva).
Souřadnice y je -2, protože je v uspořádané dvojici druhá. Nyní se posuňte o 2 jednotky záporným směrem (dolů). Když se podíváte na osu y, měli byste na této ose zarovnat souřadnici -2.
Kroky pro vykreslení bodu jsou shrnuty níže.
Kroky pro vykreslení uspořádané dvojice (x, y) v rovině souřadnic
- Určete souřadnici x. Určete souřadnici x, která se nachází v rovině souřadnic. Začněte v počátku a pohybujte se ve vodorovném směru, ve směru osy x, ve vzdálenosti dané souřadnicí x. Pokud je souřadnice x kladná, posuňte se doprava, pokud je souřadnice x záporná, posuňte se doleva.
- Určete souřadnici y. Začněte od souřadnice x a pohybujte se svisle, ve směru osy y, ve vzdálenosti dané souřadnicí y. Je-li y-ová souřadnice kladná, posuňte se nahoru; je-li y-ová souřadnice záporná, posuňte se dolů.
- Nakreslete bod na koncové místo. Označte bod uspořádanou dvojicí.
Kreslení bodů v souřadnicové rovině
Označte kvadranty a použijte je k zakreslení bodů
Protínající se osy x a y souřadnicové roviny ji rozdělují na čtyři úsečky. Tyto čtyři úseky se nazývají kvadranty. Kvadranty se pojmenovávají pomocí římských číslic I, II, III a IV počínaje pravým horním kvadrantem a dále proti směru hodinových ručiček.
Uspořádané dvojice v rámci libovolného konkrétního kvadrantu mají společné určité vlastnosti. Podívejte se na jednotlivé kvadranty v následujícím grafu. Čeho si všimnete na znaménkách souřadnic x a y bodů v jednotlivých kvadrantech?
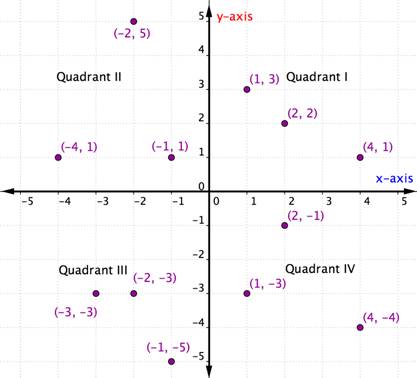
V rámci každého kvadrantu jsou znaménka souřadnic x a y každé uspořádané dvojice stejná. Řídí se také určitým vzorem, který je nastíněn v následující tabulce.
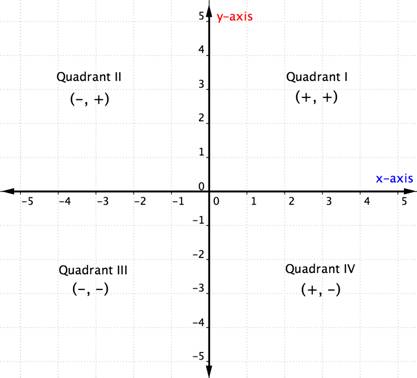
| Kvadrant | Všeobecný tvar bodu v tomto kvadrantu | Příklad | Popis |
|---|---|---|---|
| I | (+,+) | (5,4) | Vycházejte z počátku a jděte po ose x kladným směrem (doprava) a po ose y kladným směrem (nahoru). |
| II | (-,+) | (-5,4) | Vycházejte z počátku a jděte podél osy x v záporném směru (doleva) a podél osy y v kladném směru (nahoru). |
| III | (-,-) | (-5,-4) | Vycházejte z počátku a jděte podél osy x v záporném směru (vlevo) a podél osy y v záporném směru (dolů). |
| IV | (+,-) | (5,-4) | Vycházejte z počátku a jděte po ose x v kladném směru (doprava) a po ose y v záporném směru (dolů). |
Pokud znáte kvadranty v rovině souřadnic, můžete kvadrant uspořádané dvojice určit i bez grafického znázornění pohledem na výše uvedený graf. Zde je další způsob, jak o tom přemýšlet.
Následující příklad podrobně popisuje, jak určit polohu bodu v kvadrantu pouhým přemýšlením o znaménkách jeho souřadnic. Přemýšlení o kvadrantové poloze před zakreslením bodu vám může pomoci předejít chybě. Je to také užitečná znalost pro kontrolu, zda jste bod zakreslili správně.
Příklad
V kterém kvadrantu se nachází bod (-7,10)?
Příklad
V kterém kvadrantu se nachází bod (-10,-5)?
Co se stane, když uspořádaná dvojice má souřadnici x nebo y rovnou nule? Následující příklad ukazuje graf uspořádané dvojice (0,4).
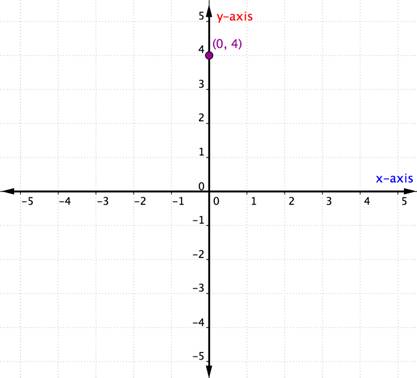
Bod ležící na jedné z os se nepovažuje za bod v kvadrantu. Leží prostě na jedné z os. Kdykoli je souřadnice x rovna 0, bod se nachází na ose y. Podobně každý bod, jehož souřadnice y je 0, se nachází na ose x.
Rozpoznejte kvadranty a použijte je k vykreslování bodů
Souhrn
Souřadnicová rovina je systém pro vykreslování a popis bodů a přímek. Souřadnicová rovina se skládá z vodorovné (x-) osy a svislé (y-) osy. Průsečík těchto přímek tvoří počátek, kterým je bod (0,0). Souřadnicová rovina je rozdělena na čtyři kvadranty. Tyto vlastnosti souřadnicového systému společně umožňují grafické znázornění a komunikaci o bodech, přímkách a dalších algebraických pojmech
.





