Begyndende algebra
Læringsmål
- Plotte ordnede par
- Identificer komponenterne i koordinatplanet
- Plotte ordnede par på koordinatplanet
- Identificere kvadranter på koordinatplanet
- Identificere de fire kvadranter i et koordinatplan
- Givet et ordnet par, bestem dets kvadrant
Koordinatplanet blev udviklet for århundreder siden (i 1637 for at være præcis) og forfinet af den franske matematiker René Descartes. Til hans ære kaldes systemet nogle gange det kartesiske koordinatsystem. Koordinatplanet kan bruges til at tegne punkter og tegne linjer. Dette system giver os mulighed for at beskrive algebraiske relationer på en visuel måde og hjælper os også med at skabe og fortolke algebraiske begreber.
Koordinatplanets komponenter
Du har sandsynligvis brugt et koordinatplan før. Har du f.eks. nogensinde brugt et gitteroverlay til at kortlægge et objekts position? (Dette gøres også ofte med vejkort.)

Dette “kort” bruger et horisontalt og vertikalt gitter til at formidle oplysninger om et objekts placering. Bemærk, at bogstaverne A-F er anført langs den øverste kant, og at tallene 1-6 er anført langs den venstre kant. Den generelle placering af ethvert objekt på dette kort kan findes ved hjælp af bogstavet og nummeret på dets gitterkvadrat. Du kan f.eks. finde den genstand, der findes på kvadratet “4F”, ved at bevæge fingeren langs den vandrette til bogstavet F og derefter lige nedad, så du er på linje med 4. Du vil finde en blå skive, der befinder sig på dette sted på kortet.
Koordinatplanet har lignende elementer som det ovenfor viste gitter. Det består af en vandret akse og en lodret akse, tallinjer, der skærer hinanden i rette vinkler. (De står vinkelret på hinanden.)
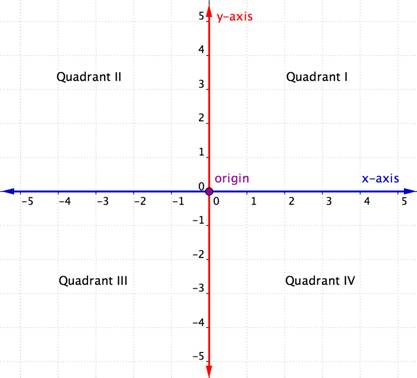
Den vandrette akse i koordinatplanet kaldes x-aksen. Den lodrette akse kaldes y-aksen. Det punkt, hvor de to akser skærer hinanden, kaldes oprindelsen. Oprindelsen ligger ved 0 på x-aksen og 0 på y-aksen.
Lokaliteter i koordinatplanet beskrives som ordnede par. Et ordnet par fortæller dig placeringen af et punkt ved at relatere punktets placering langs x-aksen (den første værdi i det ordnede par) og langs y-aksen (den anden værdi i det ordnede par).
I et ordnet par, f.eks. (x, y), kaldes den første værdi for x-koordinaten og den anden værdi for y-koordinaten. Bemærk, at x-koordinaten er anført før y-koordinaten. Da oprindelsen har en x-koordinat på 0 og en y-koordinat på 0, skrives dens ordnede par (0, 0).
Se på punktet nedenfor.

For at identificere placeringen af dette punkt skal du starte ved oprindelsen (0, 0) og bevæge dig til højre langs x-aksen, indtil du er under punktet. Kig på etiketten på x-aksen. 4 angiver, at du fra oprindelsen har bevæget dig fire enheder til højre langs x-aksen. Dette er x-koordinaten, det første tal i det ordnede par.
Fra 4 på x-aksen bevæger du dig op til punktet, og læg mærke til det tal, som det flugter med på y-aksen. 3 angiver, at du efter at have forladt x-aksen har bevæget dig 3 enheder opad i den lodrette retning, dvs. i y-aksens retning. Dette tal er y-koordinaten, det andet tal i det ordnede par. Med en x-koordinat på 4 og en y-koordinat på 3 har du det ordnede par (4, 3).
Lad os se på et andet eksempel.
Eksempel
Beskriv det viste punkt som et ordnet par.

Beskriv det punkt, der er vist som et ordnet par
Plotte punkter i koordinatplanet
Nu ved du, hvordan du kan bruge x- og y-aksen, og du kan også plotte et ordnet par. Husk blot, at begge processer starter ved oprindelsen – begyndelsen! Eksemplet, der følger, viser, hvordan man graferer det ordnede par (1,3).
Eksempel
Plottér punktet (1, 3).
I det foregående eksempel var både x- og y-koordinaten positive. Når den ene (eller begge) af koordinaterne i et ordnet par er negative, skal du bevæge dig i den negative retning langs den ene eller begge akser. Se nedenstående eksempel, hvor begge koordinater er negative.
Eksempel
Plottér punktet (-4,-2).

X-koordinaten er -4, fordi den kommer først i det ordnede par. Start ved oprindelsen, og flyt 4 enheder i negativ retning (til venstre) langs x-aksen.
Y-koordinaten er -2, fordi den kommer som nummer to i det ordnede par. Flyt nu 2 enheder i en negativ retning (nedad). Hvis du kigger over mod y-aksen, skulle du være på linje med -2 på denne akse.
Trinene til at tegne et punkt er opsummeret nedenfor.
Strin til at tegne et ordnet par (x, y) i koordinatplanet
- Determiner x-koordinaten. Begynd ved oprindelsen og bevæg dig vandret i x-aksens retning i den afstand, der er angivet ved x-koordinaten. Hvis x-koordinaten er positiv, flyttes til højre; hvis x-koordinaten er negativ, flyttes til venstre.
- Determiner y-koordinaten. Begynd ved x-koordinaten og bevæg dig lodret i y-aksens retning i den afstand, der er angivet ved y-koordinaten. Hvis y-koordinaten er positiv, bevæger du dig opad; hvis y-koordinaten er negativ, bevæger du dig nedad.
- Tegn et punkt på slutpositionen. Mærk punktet med det ordnede par.
Plotte punkter på koordinatplanet
Identificer kvadranter og brug dem til at plotte punkter
Den skærende x- og y-akse i koordinatplanet opdeler det i fire sektioner. Disse fire afsnit kaldes kvadranter. Kvadranter navngives ved hjælp af de romerske tal I, II, III og IV, idet man begynder med den øverste højre kvadrant og bevæger sig mod uret.
Ordnede par inden for en bestemt kvadrant har visse egenskaber til fælles. Se på hver kvadrant i nedenstående graf. Hvad bemærker du ved tegnene på x- og y-koordinaterne for punkterne inden for hver kvadrant?
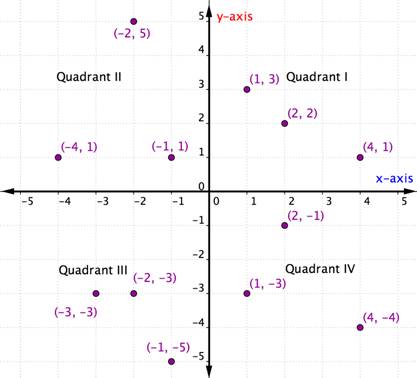
Inden for hver kvadrant er tegnene på x-koordinaterne og y-koordinaterne for hvert ordnet par de samme. De følger også et mønster, som er skitseret i nedenstående tabel.
| Kvadrant | Generel form for punkt i denne kvadrant | Eksempel | Beskrivelse |
|---|---|---|---|
| I | (+,+) | (5,4) | Gå fra oprindelsen langs x-aksen i positiv retning (til højre) og langs y-aksen i positiv retning (opad). |
| II | (-,+) | (-5,4) | Gå langs x-aksen i negativ retning (venstre) og langs y-aksen i positiv retning (opad) med udgangspunkt i oprindelsen. |
| III | (-,-) | (-5,-4) | Gå langs x-aksen i negativ retning (venstre) og langs y-aksen i negativ retning (ned) med udgangspunkt i oprindelsen. |
| IV | (+,-) | (5,-4) | Gå fra oprindelsen langs x-aksen i positiv retning (til højre) og langs y-aksen i negativ retning (nedad). |
Når du kender til kvadranterne i koordinatplanet, kan du bestemme kvadranten for et ordnet par uden selv at tegne en graf ved at se på ovenstående diagram. Her er en anden måde at tænke på det på:
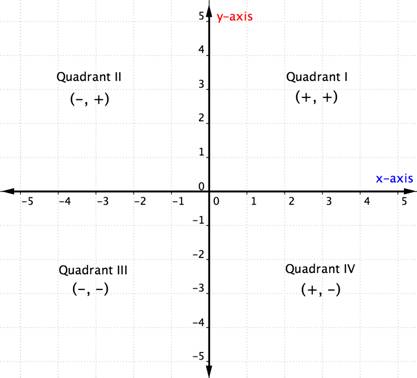
Eksemplet nedenfor beskriver, hvordan man kan bestemme kvadrantens placering for et punkt blot ved at tænke på tegnene på dets koordinater. Hvis du tænker på kvadrantplaceringen, før du plotter et punkt, kan du undgå at begå en fejl. Det er også nyttig viden til at kontrollere, at du har plottet et punkt korrekt.
Eksempel
I hvilken kvadrant er punktet (-7,10) placeret?
Eksempel
I hvilken kvadrant ligger punktet (-10,-5)?
Hvad sker der, hvis et ordnet par har en x- eller y-koordinat lig nul? Eksemplet nedenfor viser grafen for det ordnede par (0,4).
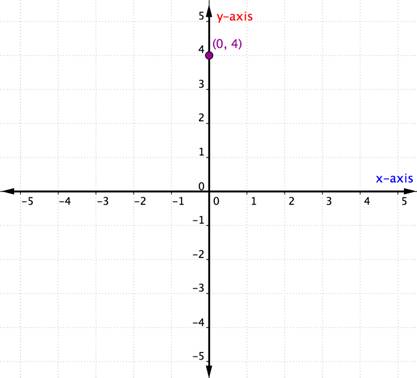
Et punkt, der ligger på en af akserne, anses ikke for at ligge i en kvadrant. Det ligger blot på en af akserne. Når x-koordinaten er 0, er punktet placeret på y-aksen. Tilsvarende vil ethvert punkt, der har y-koordinaten 0, være placeret på x-aksen.
Identificer kvadranter og brug dem til at plotte punkter
Summarum
Koordinatplanet er et system til grafisk fremstilling og beskrivelse af punkter og linjer. Koordinatplanet består af en vandret (x-) akse og en lodret (y-) akse. Skæringspunktet mellem disse linjer danner oprindelsen, som er punktet (0,0). Koordinatplanet er opdelt i fire kvadranter. Tilsammen giver disse træk ved koordinatsystemet mulighed for grafisk repræsentation og kommunikation om punkter, linjer og andre algebraiske begreber.





