Definition af bølgefunktion
Fundamentale partikler, som f.eks. elektroner, kan beskrives som partikler eller bølger.
Elektroner kan beskrives ved hjælp af en bølgefunktion. bølgefunktionens symbol er det græske bogstav psi, Ψ eller ψ.

Bølgefunktionen Ψ er et matematisk udtryk.Det bærer afgørende information om den elektron, det er forbundet med: fra bølgefunktionen får vi elektronens energi, vinkelimpuls og orbitalorientering i form af kvantetallene n, l og ml.
Bølgefunktionen kan have et positivt eller negativt fortegn.fortegnet er vigtigt i beregninger.Det er også vigtigt, når bølgefunktionerne fra to eller flere atomer kombineres til et molekyle.
Bølgefunktioner med samme fortegn (bølger i fase) vil interferere konstruktivt, hvilket fører til muligheden for binding.Bølgefunktioner med ulige fortegn (bølger ude af fase) vil interferere destruktivt.
I 1926 udledte Erwin Schrödinger bølgefunktionen for det enkleste af alle atomer, hydrogen.Løsning af Schrödinger-ligningen gør det muligt for forskere at bestemme bølgefunktioner for elektroner i atomer og molekyler.
Schrödinger-ligningen er en kvantemekanisk ligning: beregnede bølgefunktioner har diskrete, tilladte værdier for elektroner bundet i atomer og molekyler;alle andre værdier er forbudte.
Ud over Ψ’s betydning har dens kvadrat Ψ2 også en enorm betydning i kemien.
Ψ2 er sandsynlighedstætheden.Den fortæller os, hvor det er mest sandsynligt, at elektronen befinder sig i rummet omkring kernen.
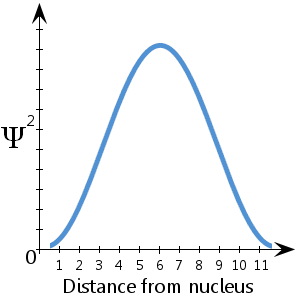
For eksempel ser vi i det (fiktive) skematiske diagram, der er plottet her, og som viser Ψ2 mod afstanden fra kernen, at det er mest sandsynligt, at elektronen befinder sig mellem ca. 5-7 enheder fra kernen. vi ser også, at der er en forsvindende lille sandsynlighed for, at elektronen befinder sig ved kernen eller mere end ca. 11½ enhed fra kernen.
Der er 100 procent sandsynlighed for, at elektronen er et eller andet sted – altså en sandsynlighed på 1.
Ψ kan kun beregnes præcist for atomer med én elektron, dvs. H, He+, Li2+, Be3+, B4+, C5+ etc. I matematisk sprogbrug siger vi, at analytiske løsninger for Ψ kun er mulige for en-elektron-systemer. en-elektron-systemer beskrives ofte som hydrogeniske – det vil sige “som hydrogen”.”
For alle andre atomer, ioner og molekyler er der ingen analytiske løsninger for Ψ mulige;tilnærmelsesmetoder er nødvendige for at beregne den.
Ψ2 og hydrogeniske orbitaler
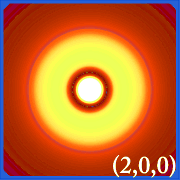
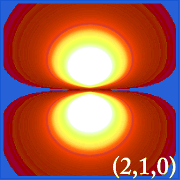
Plottet af hydrogenets sandsynlighedstæthed (i.dvs. Ψ2) for forskellige kvantetal giver os mulighed for at visualisere det rum, centreret om kernen, som elektronerne indtager.De forskellige Ψ2-fordelinger er hydrogenets elektronorbitaler.Hvilken orbital, der rent faktisk er besat, bestemmes af den mængde energi, som elektronen har.
Eksempler på brintets orbitaler