Egenskaber for kvadratiske figurer – rektangel, kvadrat, parallelogram, rombe, trapez

Egenskaber for kvadratiske figurer – rektangel, kvadrat, parallelogram, rombe, trapez

I euklidisk geometri er en kvadratisk figur en firsidet 2D-figur, hvis summen af de indre vinkler er 360°. Ordet firsidet er afledt af de to latinske ord “quadri” og “latus”, der betyder henholdsvis fire og side. Derfor er det vigtigt at identificere egenskaberne ved firkanter, når man forsøger at skelne dem fra andre polygoner.

Så, hvad er egenskaberne ved firkanter? Der er to egenskaber ved firkanter:

• En firkant skal være en lukket form med 4 sider
• Alle de indre vinkler i en firkant summerer til 360°

I denne artikel får du en idé om de 5 typer af firkanter og får kendskab til egenskaberne ved firkanter.

Det er det, du vil læse i artiklen:

• De forskellige typer af firkanter
• Rektangel
  • Rektanglernes egenskaber
  • Rektangelformler
• Firkant
  • Egenskaber af et kvadrat
  • Formler for kvadrater
• Parallelogram
  • Egenskaber ved parallellogrammer
  • Formler for parallellogrammer
• Rhombe
  • Rombers egenskaber
  • Rombers formler
• Trapezium/Trapez
  • Trapeziums egenskaber
  • Trapeziums formler

Firkanters egenskaber

Vigtige kvadrilaterale formler

Quadrilaterale spørgsmål

Her er en video, der forklarer egenskaberne ved kvadrilateraler:

Diagrammet nedenfor viser en firsidig ABCD og summen af dens indre vinkler. Alle de indre vinkler summerer til 360°.

Dermed er ∠A + ∠B + ∠C + ∠D = 360°

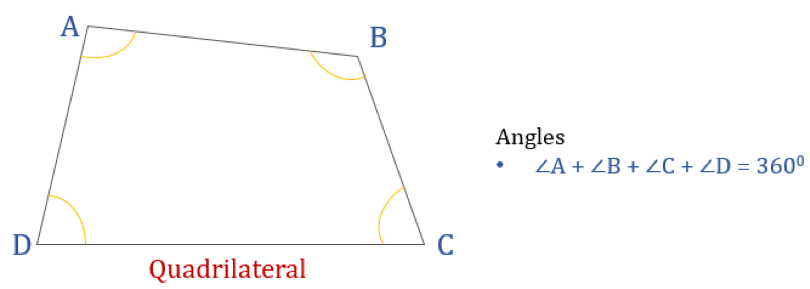
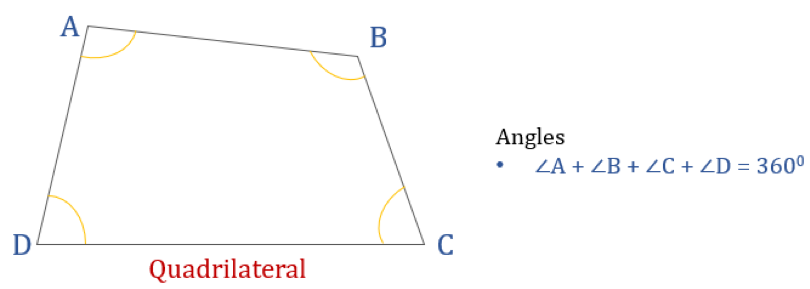
Forskellige typer af firkanter

Der findes 5 typer af firkanter på baggrund af deres form. Disse 5 firkanter er:

1. Rektangel
2. Firkant
3. Parallelogram
4. Rombus
5. Trapezium

Lad os diskutere hver af disse 5 firkanter i detaljer:

Her er spørgsmål, som vil lære dig, hvordan du kan anvende egenskaberne for alle de 5 firkanter, som du vil lære i denne artikel.

Rektangel

Et rektangel er et firkantet kvadrat med fire rette vinkler. Alle vinkler i et rektangel er således lige store (360°/4 = 90°). Desuden er de modsatte sider i et rektangel parallelle og lige store, og diagonalerne skærer hinanden i to dele.

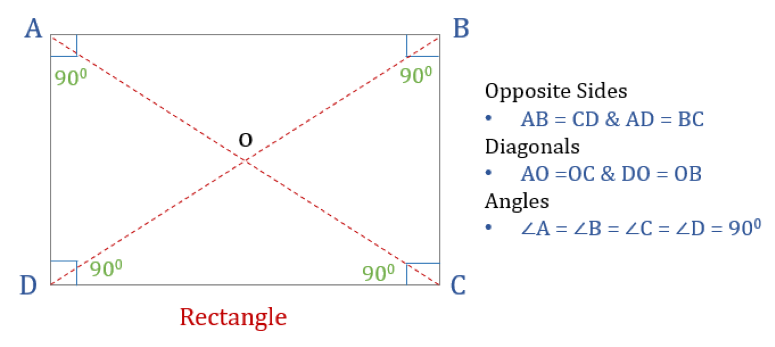
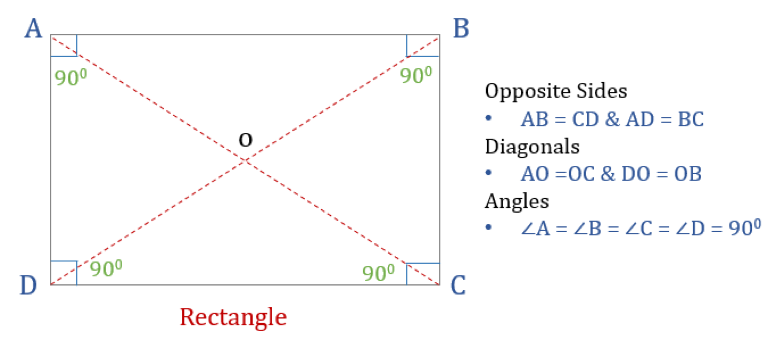
Rektangels egenskaber

Et rektangel har tre egenskaber:

• Alle vinkler i et rektangel er 90°
• De modsatte sider af et rektangel er lige store og parallelle
• Diagonalerne i et rektangel halverer hinanden

Rektangelformel – Areal og omkreds af et rektangel

Hvis længden af rektanglet er L og bredden er B, så er,

1. Aareal af et rektangel = Længde × Bredde eller L × B
2. Rektanglets omkreds = 2 × (L + B)

Disse øvelsesspørgsmål vil hjælpe dig med at størkne egenskaberne ved rektangler

Firkanter

Firkanten er en firkant med fire lige store sider og vinkler. Det er også en regulær firkant, da både dens sider og vinkler er lige store. Ligesom et rektangel har et kvadrat fire vinkler på hver 90°. Det kan også ses som et rektangel, hvis to tilstødende sider er lige store.

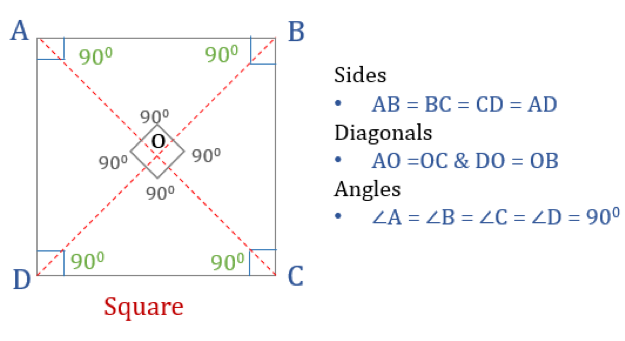
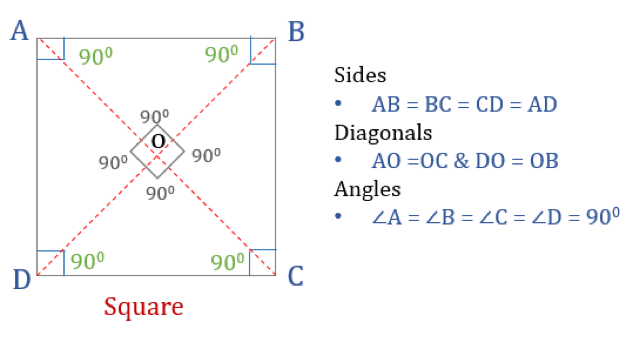
Egenskaber ved et kvadrat

For at en firkant skal være et kvadrat, skal den have visse egenskaber. Her er de tre egenskaber ved firkanter:

• Alle vinkler i et kvadrat er 90°
• Alle sider i et kvadrat er lige store og parallelle med hinanden
• Diagonalerne halverer hinanden vinkelret

Firkantformel – Areal og omkreds af et kvadrat

Hvis siden af et kvadrat er “a”, så er,

1. Firkantens areal = a × a = a²
2. Firkantens omkreds = 2 × (a + a) = 4a

Disse øvelsesspørgsmål vil hjælpe dig med at størkne egenskaberne ved firkanter

Som du scorer Q50-51 på GMAT, hjælper det dig med at få en GMAT-score på 700+. Hvorfor begynder du ikke at forberede dig til GMAT med vores gratis forberedelsesressourcer og starter din rejse for at få en Q50-51 på GMAT. Lær af Carrie Law, der forbedrede sig fra Q35 til Q50 på 3 uger.

Parallelogram

Et parallelogram er, som navnet antyder, en simpel firkant, hvis modsatte sider er parallelle. Det har således to par parallelle sider. Desuden er de modsatte vinkler i et parallelogram lige store, og dets diagonaler halverer hinanden.

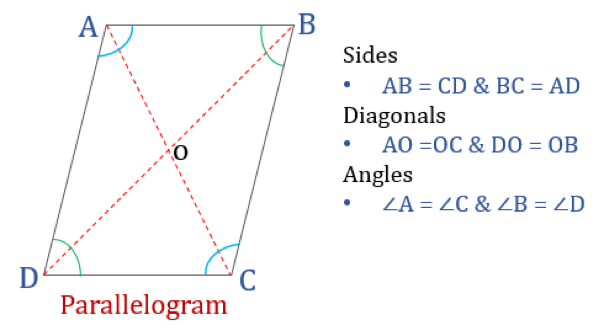
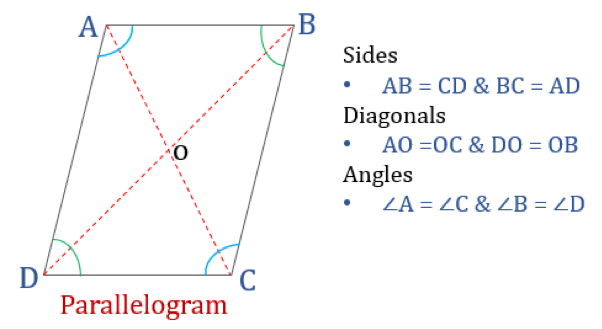
Egenskaber ved parallelogram

En firsidig, der opfylder nedenstående egenskaber, vil blive klassificeret som et parallelogram. Et parallelogram har fire egenskaber:

• De modsatte vinkler er lige store
• De modsatte sider er lige store og parallelle
• Diagonalerne halverer hinanden
• Summen af to tilstødende vinkler er 180°

Parallelogramformler – Areal og omkreds af et parallelogram

Hvis længden af et parallelogram er “l”, hvis bredden er “b” og højden er “h”, så er

1. Perimeter af parallelogram = 2 × (l + b)
2. Aarealet af parallelogrammet = l × h

Disse øvelsesspørgsmål vil hjælpe dig med at størkne egenskaberne ved parallelogrammet

Rhombus

En rhombus er en firkant, hvis alle fire sider er lige lange, og hvis modsatte sider er parallelle med hinanden. Vinklerne er dog ikke lig med 90°. En rhombe med rette vinkler ville blive til et kvadrat. Et andet navn for rhomben er “diamant”, da den ligner diamantfarven i spillekort.

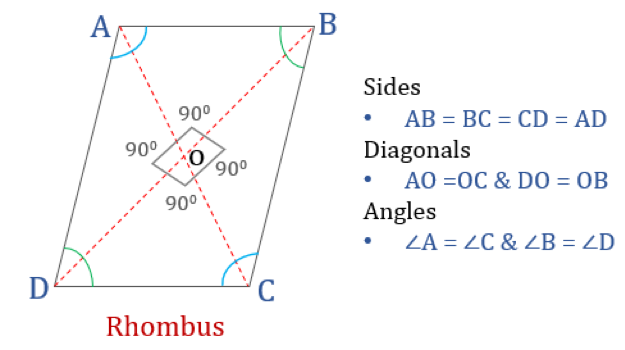
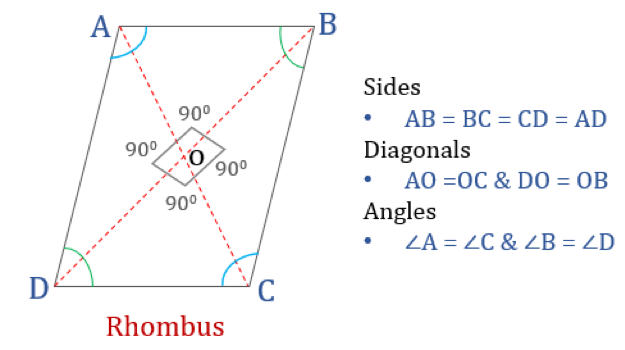
Rombens egenskaber

En rhombe er en firekant, der har følgende fire egenskaber:

• De modsatte vinkler er lige store
• Alle sider er lige store og, modsatte sider er parallelle med hinanden
• Diagonalerne halverer hinanden vinkelret
• Summen af to tilstødende vinkler er 180°

Rhombeformler – Areal og omkreds af en rhombe

Hvis siden af en rhombe er a så, omkredsen af en rhombe = 4a

Hvis længden af to diagonaler i en rhombe er d1 og d2, så er arealet af en rhombe = ½ × d1 × d2

Disse øvelsesspørgsmål vil hjælpe dig med at størkne egenskaberne ved rhomber

Trapezium

Et trapezium (kaldet Trapezoid i USA) er en firkant, som kun har ét par parallelle sider. De parallelle sider betegnes som “baser”, og de to andre sider kaldes “ben” eller sidesider.

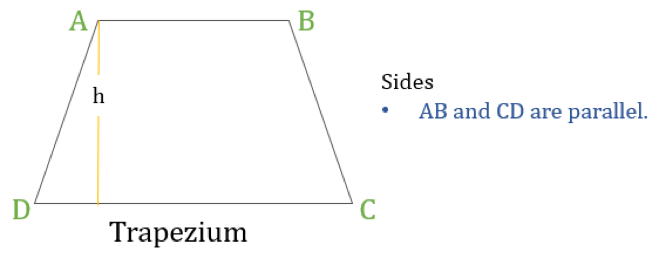
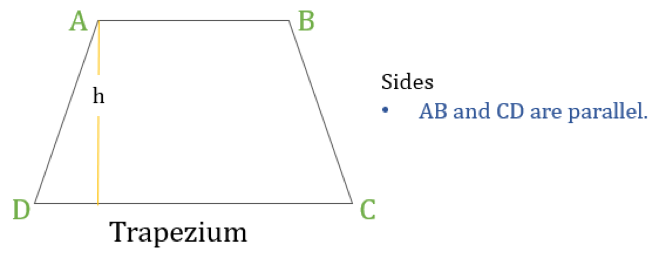
Egenskaber ved trapezium

Et trapezium er en firsidig side, hvor følgende en egenskab:

• Kun et par modsatte sider er parallelle til hinanden

Trapeziumformler – Areal og omkreds af et trapez

Hvis højden af et trapez er “h” (som vist i ovenstående diagram), så er:

1. Trapezets omkreds = Summen af længderne af alle sider = AB + BC + CD + DA
2. Trapezets areal = ½ × (summen af længderne af parallelle sider) × h = ½ × (AB + CD) × h

Disse øvelsesspørgsmål vil hjælpe dig med at størkne egenskaberne ved trapezium

Firkanternes egenskaber

Nedenstående tabel opsummerer alle egenskaberne ved de firekvadrater, som vi har lært indtil nu:

Firkanternes egenskaber	Rektangel	Firkant	Kvadrat	Parallelogram	Rhombe	Trapezium
Alle sider er lige store	✖	✔	✖	✔	✖
Modsat Siderne er lige store	✔	✔	✔	✔	✔	✖
	Overside Siderne er parallelle	✔	✔	✔	✔	✔	✔
	Alle vinkler er lige store	✔	✔	✖	✖	✖
Oversatte vinkler er lige store	✔	✔	✔	✔	✔	✔	✖
Summen af to tilstødende vinkler er 180	✔	✔	✔	✔	✖
Skærer hinanden	✔	✔	✔	✔	✖
Skærer vinkelret på hinanden	✖	✔	✖	✔	✖	✖

Det nedenstående billede opsummerer også egenskaberne ved firkanter:

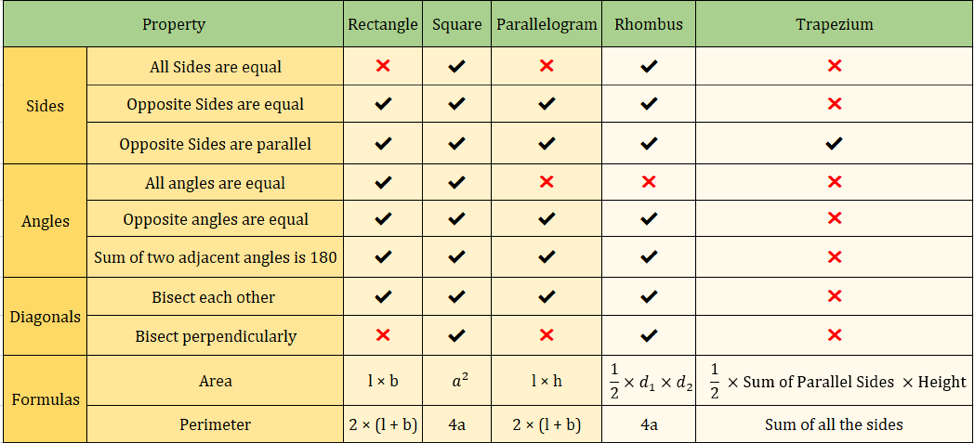
Vigtige kvadrilaterale formler

Nedenstående tabel opsummerer formlerne for areal og omkreds for forskellige typer af kvadrilaterale:

4a

	Firkantformler	Rektangel	Firkant	Parallelogram	Rhombus	Trapezium
Area	l × b	a²	l × h	½ × d1 × d2	½ × (summen af parallelle sider) × højde
Omkreds	2 × (l + b)	2 × (l + b)	4a	Summen af alle siderne

Videregående læsning:

• Cirkelens egenskaber | Cirkelformler – areal og omkreds
• Tallets egenskaber – Lige & Ulige | Primtal | HCF & LCM
• Trekantens egenskaber – Definition | Typer | Klassifikation
• Linjer og vinkler – Egenskaber og deres anvendelse

Quadrilaterale spørgsmål

Lad os øve os i at anvende egenskaberne ved kvadrilateraler på de følgende eksempler på spørgsmål:

Spørgsmål 1

Adam ønsker at bygge et hegn omkring sin rektangulære have med en længde på 10 meter og en bredde på 15 meter. Hvor mange meter hegn skal han købe for at indhegne hele haven?

1. 20 meter
2. 25 meter
3. 30 meter
4. 40 meter
5. 50 meter

Løsning

Skridt 1: Givet

• Adam har en rektangulær have.
  • Den har en længde på 10 meter og en bredde på 15 meter.
  • Han ønsker at bygge et hegn rundt om den.

Stræk 2: At finde

• Den længde, der kræves for at bygge hegnet rundt om hele haven.

Strin 3: Tilgang og udregning

Hegnet kan kun bygges rundt om havens ydersider.

• Så den samlede længde af det nødvendige hegn= Summen af længderne af alle havens sider.
  • Da haven er rektangulær, er summen af længden af alle sidernes længde intet andet end havens omkreds.
  • Perimeter = 2 × (10 + 15) = 50 meter

Dermed er den nødvendige længde af hegnet 50 meter.

Dermed er mulighed E det rigtige svar.

Spørgsmål: 2

Steve ønsker at male den ene rektangulære væg i sit værelse. Omkostningerne til at male væggen er 1,5 $ pr. kvadratmeter. Hvis væggen er 25 meter lang og 18 meter bred, hvad er så den samlede pris for at male væggen?

1. $ 300
2. $ 350
3. $ 450
4. $ 600
5. $ 675

Løsning

Strin 1: Givet

• Steve ønsker at male en væg i sit værelse.
  • Væggen er 25 meter lang og 18 meter bred.
  • Kostprisen for at male væggen er 1,5 dollar pr. kvadratmeter.

Strin 2: At finde

• De samlede omkostninger til at male væggen.

Strin 3: Tilgang og udregning

• En væg males over hele sit areal.
  • Så hvis vi finder det samlede areal af væggen i kvadratmeter og ganger det med prisen for at male 1 kvadratmeter af væggen, så kan vi den samlede omkostning.
  • Vægens areal = længde × bredde = 25 meter × 18 meter = 450 kvadratmeter
  • Den samlede omkostning for at male væggen = 450 × 1 kr.5 = 675 $

Det korrekte svar er derfor valgmulighed E.

Vi håber, at du nu har lært de forskellige typer af firkanter, deres egenskaber og formler, og hvordan du kan anvende disse begreber til at løse spørgsmål om firkanter. Anvendelsen af firkanter er vigtig for at løse geometriske spørgsmål i GMAT. Hvis du planlægger at tage GMAT, kan vi hjælpe dig med studiemateriale af høj kvalitet, som du kan få gratis adgang til ved at registrere dig her.

Her er nogle flere artikler om matematik:

1. Forbedre nøjagtigheden i matematikspørgsmål om polygoner
2. Geometri spørgsmål – de mest almindelige fejl | GMAT Quant Prep

Hvis du planlægger at tage GMAT, kan vi give dig adgang til online indhold af høj kvalitet til at forberede dig. Vi er det mest anmeldte GMAT prep firma på gmatclub med mere end 1950 anmeldelser.

Hvorfor tager du ikke en gratis prøveperiode og bedømmer selv?

Skriv til os på [email protected] i tilfælde af en forespørgsel.