En cylinders overfladeareal – Forklaring og eksempler
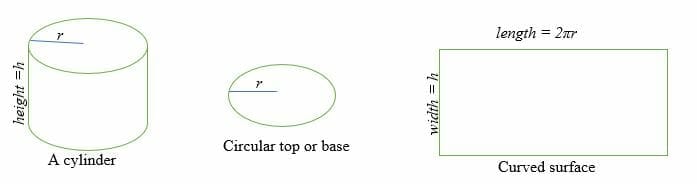
Hvor vi går i gang med emnet om en cylinders overfladeareal, skal vi gennemgå en cylinder. I geometri er en cylinder en tredimensionel figur med to cirkulære grundflader parallelle med hinanden og en krum overflade.
Hvordan finder man overfladearealet af en cylinder?
Overfladearealet af en cylinder er summen af to parallelle og kongruente cirkulære flader og det krumme overfladeareal.
Denne artikel omhandler, hvordan man finder det samlede overfladeareal og det laterale overfladeareal af en cylinder.
For at beregne en cylinders overfladeareal skal du finde grundarealet (B) og det buede overfladeareal (CSA). Derfor er overfladearealet eller den samlede overflade af en cylinder lig med summen af basisarealet gange to og arealet af den buede overflade.
Den buede overflade af en cylinder er lig med et rektangel, hvis længde er 2πr og hvis bredde er h.
Hvor r = radius af den cirkulære flade og h = cylinderens højde.
Aarealet af den krumme overflade = Arealet af et rektangel =l x w = πdh
Basisarealet, B = Arealet af en cirkel = πr2
Formel for arealet af en cylinder
Formlen for det samlede overfladeareal af en cylinder er givet som:
Total overfladeareal af en cylinder = 2πr2 + 2πrh
TSA = 2πr2 + 2πrh
Hvor 2πr2 er det øverste og nederste cirkulære overfladeareal, og 2πrh er arealet af den krumme overflade.
Gennem at tage 2πr som en fælles faktor fra RHS, får vi;
TSA = 2πr (h + r) ……………………………………. (Formel for overfladearealet af en cylinder)
Lad os løse eksempelopgaver, der involverer overfladearealet af en cylinder.
Eksempel 1
Find det samlede overfladeareal af en cylinder, hvis radius er 5 cm og højde er 7 cm.
Løsning
Med formlen,
TSA = 2πr (h + r)
= 2 x 3.14 x 5(7 + 5)
= 31,4 x 12
= 376,8 cm2
Eksempel 2
Find radius af en cylinder, hvis samlede overfladeareal er 2136,56 kvadratfod, og højden er 3 fod.
Løsning
Løsning
Givet:
TSA = 2136.56 kvadratfod
Højden, h = 3 fod
Men, TSA = 2πr (h + r)
2136,56 =2 x 3,14 x r (3 + r)
2136,56 = 6.28r (3 + r)
Ved distributiv egenskab af multiplikation på RHS har vi,
2136,56 = 18,84r + 6,28r2
Divider hvert udtryk med 6,28
340.22 = 3r + r2
r2 + 3r – 340,22 = 0 ……… (en kvadratisk ligning)
Ved løsning af ligningen ved hjælp af den kvadratiske formel får vi,
r = 17
Dermed er cylinderens radius 17 fod.
Eksempel 3
Oprisen for maling af en cylinderformet beholder er 0,04 $ pr. cm2. Find omkostningerne ved at male 20 beholdere med radius, 50 cm, og højde, 80 cm.
Løsning
Beregn det samlede overfladeareal af 20 beholdere.
TSA = 2πr (h + r)
= 2 x 3.14 x 50 (80 + 50)
= 314 x 130
= 40820 cm2
Det samlede overfladeareal af 20 containere = 40 820 cm2 x 20
=816 400 cm2
Udgifterne til maling = 816 400 cm2 x 0 $.04 pr. cm2
= $32.656.
Dermed er omkostningerne til maling af 20 containere $32.656.
Eksempel 4
Find højden af en cylinder, hvis dens samlede overfladeareal er 2552 in2 og radius er 14 in.
Løsning
Givet:
TSA = 2552 in2
Radius, r = 14 in.
Men, TSA = 2πr (h + r)
2552 = 2 x 3.14 x 14 (14 + h)
2552 = 87,92(14 + h)
Divider begge sider med 87,92 for at få,
29.026 = 14 + h
Subtraher med 14 på begge sider.
h = 15
Heraf følger, at cylinderens højde er 15 tommer.
Lateral overfladeareal af en cylinder
Som tidligere nævnt er arealet af den buede overflade af en cylinder det, der betegnes som det laterale overfladeareal. Med enkle ord er en cylinders laterale overfladeareal en cylinders overfladeareal, eksklusive arealet af bunden og bunden (cirkulær overflade).
Formlen giver en cylinders laterale overfladeareal;
LSA = 2πrh
Eksempel 5
Find det laterale overfladeareal af en cylinder, hvis diameter er 56 cm og højde er 20 cm.
Løsning
Givet:
Diameter = 56 cm, dermed radius, r =56/2 = 28 cm
Højde, h = 20 cm
Med, formlen,
LSA = 2πrh
= 2 x 3.14 x 28 x 20
= 3516,8 cm2.
Det laterale overfladeareal af cylinderen er således 3516,8 cm2.
Eksempel 6
Det laterale overfladeareal af en cylinder er 144 ft2. Hvis cylinderens radius er 7 ft, skal du finde cylinderens højde.
Løsning
Givet;
LSA = 144 ft2
Radius, r = 7 ft




