Intolkning af koefficienterne for lineær regression

Intolkning af koefficienterne for lineær regression

I dag findes der et væld af maskinlæringsalgoritmer, som vi kan afprøve for at finde den bedste løsning til vores specifikke problem. Nogle af algoritmerne har en klar fortolkning, andre fungerer som en blackbox, og vi kan bruge tilgange som LIME eller SHAP til at udlede nogle fortolkninger.

I denne artikel vil jeg gerne fokusere på fortolkningen af koefficienter i den mest grundlæggende regressionsmodel, nemlig lineær regression, herunder de situationer, hvor afhængige/uafhængige variabler er blevet transformeret (i dette tilfælde taler jeg om logtransformation).

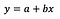
Jeg antager, at læseren er bekendt med lineær regression (hvis ikke findes der en masse gode artikler og Medium-indlæg), så jeg vil udelukkende fokusere på fortolkningen af koefficienterne.

Den grundlæggende formel for lineær regression kan ses ovenfor (jeg har med vilje udeladt residualerne, for at holde tingene enkle og kortfattet). I formlen betegner y den afhængige variabel, og x er den uafhængige variabel. Lad os for enkelhedens skyld antage, at der er tale om univariat regression, men principperne gælder naturligvis også for det multivariate tilfælde.

For at sætte det i perspektiv, lad os sige, at vi efter tilpasning af modellen får:

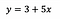
Intercept (a)

Jeg vil opdele fortolkningen af interceptet i to tilfælde:

x er kontinuert og centreret (ved at trække middelværdien af x fra hver observation bliver gennemsnittet af det transformerede x 0) – gennemsnittet y er 3, når x er lig med stikprøvens middelværdi x er kontinuert, men ikke centreret – gennemsnittet y er 3, når x = 0 x er kategorisk – gennemsnittet y er 3, når x = 0 (denne gang angiver en kategori, mere om dette nedenfor)

Koefficient (b)

x er en kontinuert variabel

Interpretation: en stigning på en enhed i x resulterer i en stigning i gennemsnitlig y med 5 enheder, alle andre variabler holdes konstante.

x er en kategorisk variabel

Dette kræver en lidt større forklaring. Lad os sige, at x beskriver køn og kan antage værdier (“mand”, “kvinde”). Lad os nu konvertere den til en dummy-variabel, der tager værdierne 0 for mænd og 1 for kvinder.

Interpretation: Gennemsnitlig y er højere med 5 enheder for kvinder end for mænd, alle andre variabler holdes konstante.

Log-niveau-model

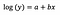
Typisk bruger vi logtransformation til at trække udestående data fra en positivt skæv fordeling tættere på hovedparten af dataene, for at gøre variablen normalfordelt. I tilfælde af lineær regression er en yderligere fordel ved at bruge logtransformationen fortolkeligheden.

Som før, lad os sige, at nedenstående formel præsenterer koefficienterne for den tilpassede model.

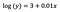
Intercept (a)

Interpretationen svarer til vaniljetilfældet (niveauniveau), dog skal vi tage eksponenten af interceptet til fortolkning exp(3) = 20,09. Forskellen er, at denne værdi står for det geometriske gennemsnit af y (i modsætning til det aritmetiske gennemsnit i tilfælde af niveauniveaumodellen).

Koefficient (b)

Principperne svarer igen til niveauniveaumodellen, når det drejer sig om fortolkning af kategoriske/numeriske variabler. Analogt til interceptet skal vi tage eksponenten af koefficienten: exp(b) = exp(0,01) = 1,01. Det betyder, at en enhedsstigning i x medfører en stigning på 1 % i den gennemsnitlige (geometriske) y, idet alle andre variabler holdes konstante.

To ting er værd at nævne her:

Der er en tommelfingerregel, når det gælder om at fortolke koefficienter i en sådan model. Hvis abs(b) < 0,15 er det ret sikkert at sige, at når b = 0,1 vil vi observere en stigning på 10 % i y for en enhedsændring i x. For koefficienter med større absolut værdi anbefales det at beregne eksponenten. Når der er tale om variabler i interval (som f.eks. en procentdel) er det mere praktisk for fortolkningen at først gange variablen med 100 og derefter tilpasse modellen. På denne måde er fortolkningen mere intuitiv, da vi øger variablen med 1 procentpoint i stedet for 100 procentpoint (fra 0 til 1 med det samme).

level-log model

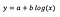
Lad os antage, at vi efter tilpasning af modellen får:

Interpretationen af interceptet er den samme som i tilfældet med modellen på niveauniveau.

For koefficienten b – en stigning på 1 % i x resulterer i en omtrentlig stigning i det gennemsnitlige y med b/100 (0,05 i dette tilfælde), idet alle andre variabler holdes konstante. For at få det nøjagtige beløb skal vi tage b× log(1,01), hvilket i dette tilfælde giver 0,0498.

log-log-model

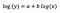
Lad os antage, at vi efter tilpasning af modellen får:

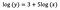
Igen fokuserer jeg på fortolkningen af b. En stigning i x med 1 % resulterer i en stigning på 5 % i den gennemsnitlige (geometriske) y, idet alle andre variabler holdes konstante. For at få det nøjagtige beløb skal vi tage

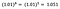
hvilket er ~5,1%.

Konklusioner

Jeg håber, at denne artikel har givet dig et overblik over, hvordan man fortolker koefficienter af lineær regression, herunder de tilfælde, hvor nogle af variablerne er log-transformeret. Som altid er enhver konstruktiv feedback velkommen. Du kan henvende dig til mig på Twitter eller i kommentarerne.