Sandsynlighed Introduktion: Artikler og videoer med løsninger!
 Det at kaste terninger, finde en parkeringsplads, vinde i kortspil; Det er blot nogle situationer, hvor du måske ønsker at finde oddsene for, at en begivenhed sker. Hvis du vil vide, hvordan man finder sandsynligheden, skal du først finde ud af, hvilken slags spørgsmål du har. Det er f.eks. noget andet at finde sandsynligheden for, at en begivenhed finder sted, end at finde sandsynligheden for, at gruppemedlemmer vælger den samme ting.
Det at kaste terninger, finde en parkeringsplads, vinde i kortspil; Det er blot nogle situationer, hvor du måske ønsker at finde oddsene for, at en begivenhed sker. Hvis du vil vide, hvordan man finder sandsynligheden, skal du først finde ud af, hvilken slags spørgsmål du har. Det er f.eks. noget andet at finde sandsynligheden for, at en begivenhed finder sted, end at finde sandsynligheden for, at gruppemedlemmer vælger den samme ting.
Nogle sandsynligheder er lette at identificere, f.eks. at finde sandsynligheden for at kaste terninger eller vælge fra et sæt kort.
Spørgsmål, der involverer binomialteoremet, er også lette at identificere. I disse typer eksperimenter er de eneste mulige resultater af en hændelse “succes” eller “fiasko”: som ja/nej, hoved/hale eller sort/hvid.
Andre spørgsmålstyper, du kan støde på, involverer personer, som:
- Vælgelse af en person fra en gruppe eller et udvalg.
- Sandsynligheden for, at en gruppe vælger det samme.
Hændelser
Vil du finde sandsynligheden for, at en simpel begivenhed sker? Som f.eks. at det regner, eller at finde en parkeringsplads i byen? Se:
Sandsynligheden for, at en simpel begivenhed indtræffer.
Hvis du derimod ønsker det stik modsatte, skal du se:
Sådan finder du sandsynligheden for, at en begivenhed IKKE indtræffer.
Har du et spørgsmål om, at en begivenhed indtræffer i betragtning af en anden begivenhed? Som f.eks. sandsynligheden for at finde en parkeringsplads, givet at det er spilledag, eller for at finde et bestemt populært legetøj på Black Friday? Hvis det er tilfældet, skal du tjekke:
- Odds for en begivenhed, givet en anden begivenhed.
- To begivenheder, der forekommer sammen.
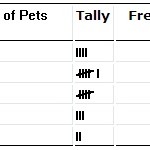
En frekvensfordelingstabel.
Frekvensfordelinger
Har du en frekvensfordeling at arbejde med? Eller er du i stand til at lave en frekvensfordelingstabel med dine givne data? Du har f.eks. x antal genstande med en bestemt egenskab. Sandsynlighedsfrekvensfordeling.
Introduktion til sandsynlighed: How-to artikler og videoer.
- Permutationer og kombinationer: Sådan løser du problemer
- Probability Problems: Løs dem på den nemme måde!
- Sandsynlighed for a og b.
- Total sandsynlighedsregel.
- Bayes-sætnings-problemer: Nemme løsningsskridt.
- Prior sandsynlighed (herunder uinformativ og konjugeret).
- Sådan laver du en sandsynlighedsfordeling ud fra data.
- Sådan finder du sandsynligheden for at vælge en person fra en gruppe eller et udvalg.
- Sådan finder du sandsynligheden for, at en begivenhed IKKE indtræffer.
- Sandsynlighedsfrekvensfordeling.
- Sådan finder du sandsynligheden for, at en simpel begivenhed indtræffer.
- Randombegivenhed: Sandsynlighed givet en procentdel.
- Sådan finder man sandsynligheden for, at gruppemedlemmer vælger den samme ting.
- Sådan finder man sandsynligheden for, at to afhængige hændelser indtræffer sammen.
- Sådan finder man sandsynligheden for, at en hændelse indtræffer, givet en anden hændelse.
- Sådan bruger du et sandsynlighedstræ (beslutningstræ) til at beregne odds.
- Sådan finder du sandsynligheden for at trække et kort fra et kortspil.
- Sådan finder du ud af, om noget er en gensidigt udelukkende begivenhed.
- Sådan kan du se forskellen på afhængige og uafhængige begivenheder.
- Sandsynlighed: Tørrekast.
- Sådan tegner du et Venn-diagram.
- Sådan laver du et Euler-diagram.
- 5 vælg 3: Sådan løser du kombinationer.
- Sådan bruger du det grundlæggende tælleprincip.
- Sådan finder du den forventede værdi for en diskret tilfældig variabel.
Introduktion til sandsynlighed: Definitioner
- Axiomatisk sandsynlighed.
- Benford’s lov
- Hvad er et binomialforsøg?
- Basissatser og basissatsfejl
- Brier-scorer
- Kollektivt udtømmende
- Hvad er kombinationer?
- Komplementære hændelser.
- Konditionel forventning
- Hvad er betinget relativ hyppighed?
- Tællelig additivitet
- Tomt sæt
- Epistemisk sandsynlighed
- Hændelsesrum.
- Hvad er eksperimentel sandsynlighed?
- Sammenfaldende sandsynlighedsfordelinger.
- Begrænsende fordeling.
- Maximum Likelihood Estimation
- Memoryless Property.
- Monte Carlo Method.
- Monty Hall Problem
- Hvad er en Mutually Exclusive Event?
- Hvad er en Mutually Inclusive Events?
- Gensidigt uafhængige og parvis uafhængige.
- Hvad er multiplikationsreglen?
- Nash-ligevægt
- Indetomme mængder
- Øvelsesopgaver om normal sandsynlighed.
- Hvad er en normal sandsynlighedsplot?
- Objektiv sandsynlighed
- Hvad er oddsforholdet?
- Prediktiv analyse
- Hvad er en sandsynlighedsfordelingstabel?
- Sandsynlighedsmåling
- Hvad er et sandsynlighedsrum?
- Sandsynlighedsvektorer
- Hvad er prøveområder?
- Stokastiske modeller.
- Hvad er subjektiv sandsynlighed?
- Hvad er teoretisk sandsynlighed?
- Hvad er en urnemodel?
Beregnere.
- Online permutationsberegner og kombinationsberegner.
Sandsynlighedsformler / Sandsynlighedsregler
En af de mest ubehagelige ting, som eleverne ikke bryder sig om ved formler, er manglen på dem i sandsynlighed og statistik. Der er nogle få hæfteklammer, herunder nogle notationer, som man skal kende:
Sandsynlighedsområde
0 ≤ P(A) ≤ 1
Dette angiver, at sandsynligheden for en begivenhed ligger et sted mellem nul og 100 % (som decimaltal er det 0 og 1). Du skal huske denne regel, når du adderer eller multiplicerer sandsynligheder for hændelser. Hvis dit svar er over 100 %, er det et tegn på, at du måske har gjort noget forkert.
Regel om komplementære hændelser
P(AC) + P(A) = 1
Komplementære hændelser sker, når der kun er to udfald, f.eks. ved at slå med en mønt. At kaste en terning for at se, om man får en sekser, er også komplementært; de eneste to udfald er at få en sekser (1/6 chance) eller ikke at få en sekser (5/6 chance). De to sandsynligheder skal tilsammen give 1.
Du kan også se denne formel skrevet således:
p(A) + p(A’) = 1
som algebraisk kan omlægges til:
p(A’) = 1 – p(A).
Alle tre formler er ækvivalente: hvilken terminologi (A’ eller Ac) der anvendes, er op til lærebogens forfatter og lærer. Personligt foretrækker jeg A’, som jeg kalder “ikke A”. Sandsynligheden for “ikke A” er efter min mening lettere at forstå end “komplementet” (enten sker en begivenhed, eller også sker den ikke).
Additionsregel
P(A∪B) = P(A) + P(B) – P(A∩B)
hvor ∪ er foreningen, og ∩ er skæringspunktet.
Hvad dette siger (på engelsk!) er sandsynligheden for, at begivenhed A ELLER begivenhed B sker (eller begge på samme tid) er:
- Sandsynligheden for, at begivenhed A sker alene,
- Plus sandsynligheden for, at begivenhed B sker alene,
- Plus sandsynligheden for, at begge begivenheder sker på samme tid.
Hvis man har begivenheder, der udelukker hinanden, så kan P(A∩B) ikke ske (begivenhederne kan ikke ske sammen), så formlen bliver:
P(A∪B) = P(A)+P(B)- 0 = P(A)+P(B)
Disjunkte hændelser
Hændelserne A og B er disjunkte, hvis:
P(A∩B) = 0
Det er blot en anden måde at sige, at hændelserne udelukker hinanden gensidigt. De kan ikke ske på samme tid.
En beslægtet formel er P((A∪B)c) eller tilsvarende ((A∪B)’). På engelsk hedder det “not the union”. For at løse dette skal man regne foreningen ud og tage resultatet væk fra 1 (fordi sandsynligheden for, at hændelserne sker eller ikke sker, skal summere til 1).
Konditionel sandsynlighed
P(A|B) = P(A∩B) / P(B)
Symbolet “|” betyder “givet at”. Med andre ord, sandsynligheden for, at begivenhed B indtræffer, givet at begivenhed A indtræffer. For eksempler på, hvordan man bruger formlen, se: betinget sandsynlighed.
Bayes formel
P(A|B) = P(B|A) – P(A) / P(B)
Bayes’ teorem er en måde at regne den betingede sandsynlighed ud på, selv om den er lidt mere nuanceret. Kort fortalt giver det dig den faktiske sandsynlighed for en begivenhed givet oplysninger om test. Hvad er f.eks. sandsynligheden for, at du har kræft, hvis din medicinske test er positiv (svaret = meget lavere, end du tror). For nogle eksempler, se: Bayes Theorem Eksempler og Posteriorfordelinger / Posterior Sandsynligheder.
Uafhængige hændelser
Hændelserne A og B er uafhængige, hvis den ene af dem ikke påvirker sandsynligheden for den anden. Begivenheder siges også at være uafhængige, hvis følgende ligning gælder:
P(A∩B) = P(A) – P(B).
Denne ligning er afledt af multiplikationsreglen, som siger, at P(A∩B) = P(A) * P(B|A). Da vi ved, at P(B|A) = P(B) for uafhængige hændelser, kan vi erstatte P(B|A) med P(B), hvilket giver os formlen.
Nogle bemærkninger om sandsynlighedsregler
Statistik handler om tilfældigheder og ballparking, ikke om absolutter og det “rigtige svar”. Se bare en Gallup-undersøgelse – de er sjældent mere end 90 % sikre på, at de har det “rigtige svar”. Der er teknikker, man kan bruge til at regne odds ud (f.eks. multiplicere to sandsynligheder med hinanden eller lægge dem sammen). Men bortset fra måske binomialfordelingstabellen og ovenstående formler (som i virkeligheden ikke bruges så meget) findes der ikke rigtig nogen sandsynlighedsformler, som man let kan anvende. Du er nødt til at vende tilbage til det gamle grundskoleelement, logik (du husker det… det var der lige før de begyndte at standardisere testning af logikken i dig).
De tre regler for sandsynlighedsformler:
- Der findes ingen regler (altså, meget få, bortset fra dem, der er nævnt ovenfor).
- Brug logik, ikke ligninger.
- Der er mange, mange forskellige måder at komme frem til svaret på – og ingen af dem bruger egentlig formler.
Her er et spørgsmål, der kom ind i min indbakke i morges, og som omhandler sandsynligheder:
“Hvis du forsøger at samle 6 baseballkort, der kom i pakker med cheese puffs, hvis du antager, at de er jævnt fordelt, hvor mange pakker cheese puffs vil du så forvente at skulle købe, før du har alle 6 kort?”
Strin 1 til løsning af dette problem er at indse, at du ikke kan slå svaret op i en tabel. For at løse det skal du tænke som et barn.
Kort nr. 1:Du er 8 år gammel igen og går ind i en butik med penge nok til at købe en pose ostepuffer. Du håber at samle alle 5 baseballkort, men du har ikke nogen endnu. Hvad er chancen for, at du køber en pose og får et kort, du ønsker?
Svaret er naturligvis 100 %. Hvis du køber din første pose, har du 100 % chance for, at der er et kort i posen, som du ønsker.
Kort nr. 2: Nu bliver det lidt vanskeligere. Du vender tilbage til butikken for at hente kort nr. 2. Men da du allerede har fået kort nr. 1, Mickey Mantle. Du vil ikke have ham igen, men der er en 1/5 chance for, at du får ham (og derfor en 4/5 chance for, at du ikke får ham). Hvor mange poser cheese puffs skal du købe for at få kort nr. 2 bliver et forholdsproblem. Du kan regne det ud i dit hoved, men hvis du vil modellere det matematisk, er du nødt til at opstille ligningen. Hvis en pose cheese puffs giver dig 80 % chance for at få det ønskede kort, hvor mange poser skal du så købe for at få 100 % chance?
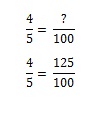
For at få 100 % skal du købe 1,25 poser.
Kort nr. 3: Oddsene begynder at blive sværere. Du har en chance på 60 % for at få det tredje baseballkort, og du skal købe 1,667 poser for at få det tredje kort.
Kort nr. 4:Oddsene begynder at blive lidt dystre. Du har 40 % chance for at få det fjerde baseballkort, og du skal købe 2,5 poser for at få det tredje kort.
Kort nr. 5:Oddsene er imod dig. Du har 20 % chance for at få det sidste kort, og du skal købe 5 poser for at få det tredje kort.
Så det samlede antal poser, du skal købe, er lig med:
1 + 1,25 + 1,667 + 2,5 + 5
Men vent! (Og her kommer en smule logik ind i billedet). Du kan ikke gå ind i en butik og købe 1,25 poser ostepuffer, så du bliver nødt til at runde op. Ligningen bliver:
1 + 2 + 2 + 2 + 3 + 5 = 13 poser.
En vigtig pointe i forbindelse med formler: Husk, at intet er absolut. Jeg er rimelig sikker på, at hvis du købte 13 poser ostepuffer, og hvis du antager, at kortene er jævnt fordelt, at du ville få alle 5 kort. Men… sandsynlighed handler om tilfældigheder, og det kunne være uheldigt at få det samme kort 10 gange i træk (det husker jeg, at det skete for mig som barn). Men der kunne være en anden forklaring på dit “uheld”, og det er, at virksomhederne ønsker, at du skal købe så mange poser som muligt, så de vil forsøge at få oddsene til at virke til deres fordel. Selv hvis kortene er ligeligt fordelt, kan selskabet sende poser med kort nr. 1, 2 og 3 til en butik (og dermed lokke dig til at samle mere end halvdelen af kortene) og nr. 4 og 5 til en anden butik.
Hvilke andre måder kan du komme i tanke om, at producenterne kan vende oddsene til deres fordel?
Sandsynligheden for, at en gruppe vælger det samme
Sandsynlighedsspørgsmål kan opdeles i forskellige typer. Når du bliver bedt om at finde sandsynligheden for, at en gruppe vælger det samme, tager du hensyn til de handlinger, som tilfældige medlemmer af en gruppe foretager (det kan være så lille som et udvalg, eller det kan være så stort som befolkningen i USA).
Disse sandsynlighedsspørgsmål giver dig en gruppe og beder dig om at beregne sandsynligheden for, at en begivenhed indtræffer for et bestemt antal tilfældige medlemmer inden for denne gruppe.
Sandsynligheden for, at en gruppe vælger den samme ting : trin
Stikprøveproblem: Der er 200 personer til en bogmesse. 159 af dem vil købe mindst én bog. Hvis du undersøger 5 tilfældige personer, der kommer ud af døren, hvad er sandsynligheden for, at de alle vil have købt mindst én bog?

Hvad er sandsynligheden for, at en gruppe køber mindst én bog?
Strap 1: Omregn dataene i spørgsmålet til en brøk. F.eks. kan sætningen “159 personer ud af 200” omdannes til: 159/200.
Stræk 2: Multiplicer brøken med sig selv. Gentag for det antal tilfældige elementer (dvs. personer), der vælges, uanset hvor mange tilfældige elementer (dvs. personer) der vælges. I vores eksempel har vi 5 adspurgte personer, så vi ønsker:
159/200 x 159/200 x 159/200 x 159/200 x 159/200 x 159/200 x 159/200 x 159/200 = 0,3176
Sådan finder man sandsynligheden for, at en gruppe vælger det samme!
Tip: Det kan være nemmere at konvertere brøken til et decimaltal, før du multiplicerer. I dette tilfælde er 159/200 = 0,795.
Kig på vores YouTube-kanal for at få mere hjælp og tips om statistik! Vi har videoer til de mest almindelige problemer, som du sandsynligvis vil støde på. Plus videoer om brug af Excel til statistik > alt fra fremstilling af grundlæggende søjlediagrammer til løsning af komplekse dataanalyseproblemer.
Stephanie Glen. “Sandsynlighed Introduktion: Artikler og videoer med løsninger!” Fra StatisticsHowTo.com: Elementær statistik for resten af os! https://www.statisticshowto.com/probability-and-statistics/probability-main-index/
——————————————————————————
Har du brug for hjælp til en lektieløsning eller et spørgsmål til en prøve? Med Chegg Study kan du få trin-for-trin-løsninger på dine spørgsmål fra en ekspert på området. Dine første 30 minutter med en Chegg-underviser er gratis!




