Syntetisk divisionsmetode
Jeg må sige, at syntetisk division er den mest “sjove” måde at dividere polynomier på. Den har færre trin for at nå frem til svaret sammenlignet med den lange divisionsmetode for polynomier. I denne lektion vil jeg gennemgå fem (5) eksempler, som forhåbentlig vil gøre dig fortrolig med de grundlæggende procedurer for en vellykket division af polynomier ved hjælp af syntetisk division.
Ting, du skal huske:
- Sørg for, at dividende er i standardform. Det betyder, at potenserne er i faldende rækkefølge.
- Divisoren skal være i formen x – \venstre( c \højre).
Eksempler på, hvordan man dividerer polynomier ved hjælp af syntetisk division
Eksempel 1: Divider nedenstående polynomium.
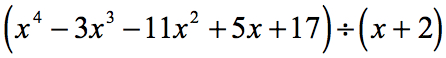
Lad os gennemgå den givne opgave igen og foretage de nødvendige justeringer, hvis det er nødvendigt.
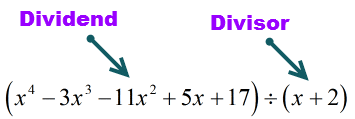
Dividenden (det, der skal divideres) er i standardform, fordi eksponenterne er i aftagende orden. Det er godt!
Divideren skal omskrives som
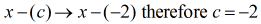
På dette tidspunkt kan jeg nu opstille den syntetiske division ved at udtrække dividendets koefficienter og derefter lægge dem på linje ovenpå.
Direkte til venstre side placeres værdien af c = – 2 inden for “kassen”.
Slutteligt konstrueres en vandret linje lige under dividendkoefficienterne.
Strin:
1. Drop den første koefficient under den vandrette linje.
2. Multiplicer det tal, du dropper, med tallet i “kassen”. Uanset dets produkt placerer du det over den vandrette linje lige under den anden koefficient.
3. Læg talkolonnen sammen, og placer derefter summen direkte under den vandrette linje.
4. Gentag processen, indtil du løber tør for kolonner at lægge sammen.
Se den animerede løsning nedenfor:
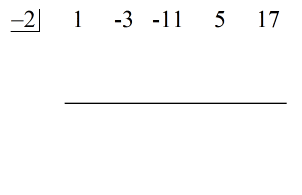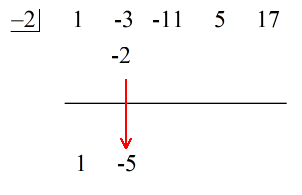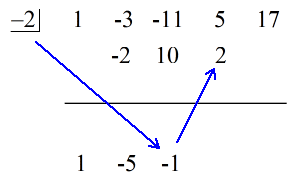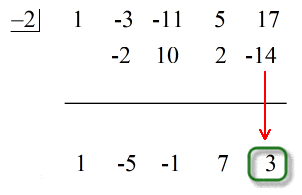
Det sidste tal under den vandrette linje er altid resten! Resten af denne opgave er 3.
Så hvordan præsenterer vi vores endelige svar?
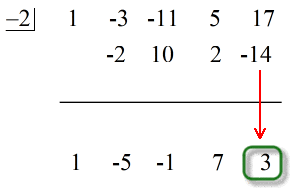
- Vis dit endelige svar i formen
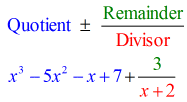
Bemærk, at tallene under den vandrette linje undtagen det sidste (resten) er koefficienterne i kvotienten.
Dertil kommer, at eksponenterne for kvotientens variabler alle er reduceret med 1.
Eksempel 2: Divider polynomiet.
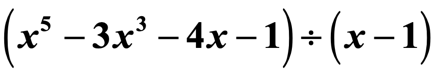
Dette er ikke et trickspørgsmål. Bemærk, at kvotienten ikke har alle eksponenterne for variablen x.
Jeg kan se, at vi mangler {x^4} og {x^2}. For at medtage alle koefficienterne af variablen x i aftagende potens skal vi omskrive den oprindelige opgave på følgende måde. Vedhæft nuller på de manglende x’er. Udtryk også divisoren som x – (c), hvilket tydeligt afslører værdien af c, dvs. c = + 1.
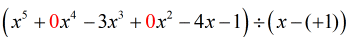
Fra dette punkt kan jeg nu opstille tallene for at fortsætte processen.
Strin:
1. Drop den første koefficient under den vandrette linje.
2. Multiplicer det tal, du dropper, med tallet i “kassen”. Uanset dets produkt placerer du det over den vandrette linje lige under den anden koefficient.
3. Læg kolonnen af tal sammen, og placer derefter summen direkte under den vandrette linje.
4. Gentag processen, indtil du løber tør for kolonner at lægge sammen.
Se den animerede løsning nedenfor:
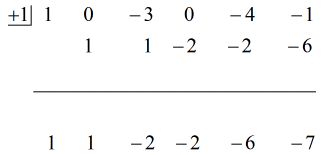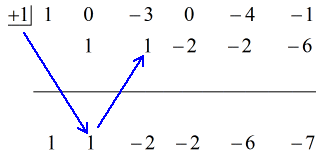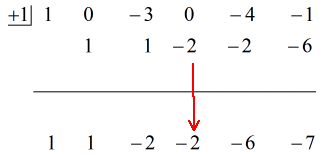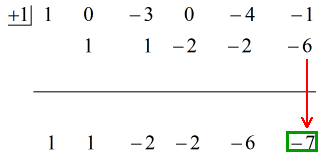
Så ved at sætte det endelige svar på formen
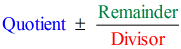
har vi
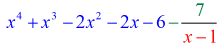
Eksempel 3: Divider polynomiet nedenfor.
\left( { – 2{x^4} + x} \right) \div \left( {x – 3} \right)
Det her bliver mere interessant! Kvotienten ser helt sikkert forfærdelig ud, fordi der mangler en masse. Ikke alene mangler den nogle x’er, som er {x^3} og {x^2}, men konstanten er også væk.
For at rette op på dette vil jeg omskrive det oprindelige problem på en sådan måde, at der er taget højde for alle x’er. Men vigtigere er det, at man ikke glemmer at medregne den manglende konstant, som er nul.
Det “nye og forbedrede” problem skal se således ud:
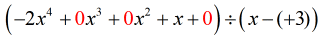
Herfra skal man fortsætte med trinene som sædvanligt.
Strinene:
1. Drop den første koefficient under den vandrette linje.
2. Multiplicer det tal, du dropper, med tallet i “kassen”. Uanset dets produkt placerer du det over den vandrette linje lige under den anden koefficient.
3. Læg kolonnen af tal sammen, og placer derefter summen direkte under den vandrette linje.
4. Gentag processen, indtil du løber tør for kolonner at lægge sammen.
Se den animerede løsning nedenfor:
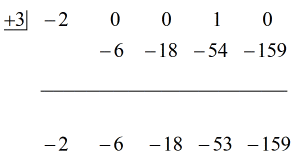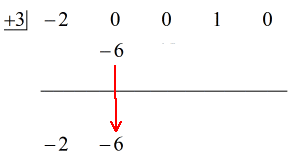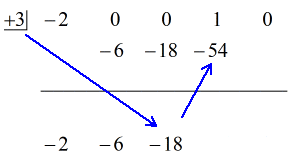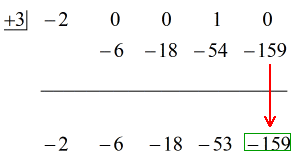
Okay så, det endelige svar til dette er
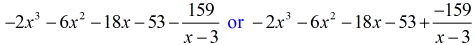
Du kan skrive det endelige svar på to måder. Den første er ved at bruge minus- eller subtraktionssymbolet for at angive, at resten er negativ. Den anden er at bruge +-symbolet, men vedhæfte et negativt symbol til tælleren. De betyder det samme!
Eksempel 4: Dividér nedenstående polynomium.
\left( { – {x^5} + 1} \right) \div \left( {x + 1} \right)
Du skal ikke lade dig nedslå af denne opgave. Det er faktisk ret nemt, især nu, hvor du allerede har gennemgået et par eksempler. Husk altid at “udfylde de manglende dele”, ikke sandt?
Opmærksomheden henledes på dividende, og du burde være enig i, at de manglende dele er {x^4}, {x^3}, {x^2} og x.
Ved at omskrive det oprindelige problem, der er klar til syntetisk division, får vi…
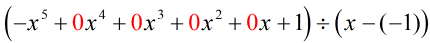
Vi har udfyldt de manglende x’er med nuller og løser eksplicit for c = -1.
Stræk:
1. Drop den første koefficient under den vandrette linje.
2. Multiplicer det tal, du dropper, med tallet i “kassen”. Uanset dets produkt placerer du det over den vandrette linje lige under den anden koefficient.
3. Læg tallene i kolonnen sammen, og placer summen direkte under den vandrette linje.
4. Gentag processen, indtil du løber tør for kolonner at lægge sammen.
Se den animerede løsning nedenfor:
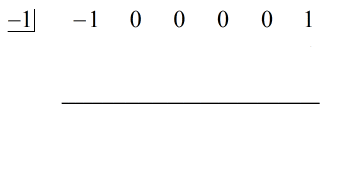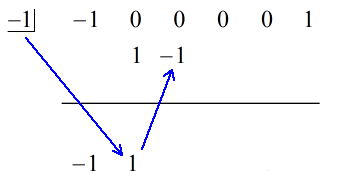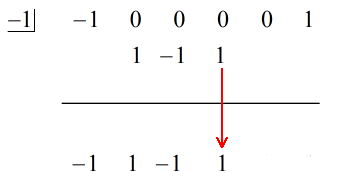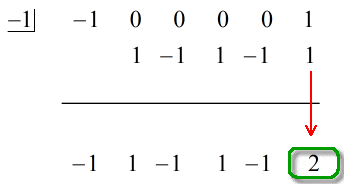
Det sidste tal under den vandrette linje vil altid være resten. Det må du ikke glemme. I dette tilfælde er resten lig med 2.
Vores endelige svar er
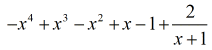
Eksempel 5: Divider polynomiet med et binomium.
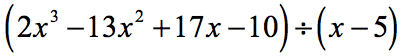
I dette eksempel vil vi få en rest på nul. Når det sker, bliver divisoren en faktor af dividend. Med andre ord, divisoren deler dividende lige meget.
Ved at undersøge opgaven kan jeg se, at der ikke mangler nogen komponenter. Der er taget højde for alle potenser af x’er, og vi har en konstant. Det er fantastisk! Denne opgave er faktisk klar til syntetisk division.
Strin:
1. Drop den første koefficient under den vandrette linje.
2. Multiplicer det tal, du dropper, med tallet i “kassen”. Uanset dets produkt placerer du det over den vandrette linje lige under den anden koefficient.
3. Læg kolonnen af tal sammen, og placer derefter summen direkte under den vandrette linje.
4. Gentag processen, indtil du løber tør for kolonner at lægge sammen.
Se den animerede løsning nedenfor:
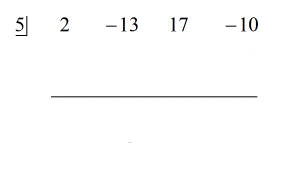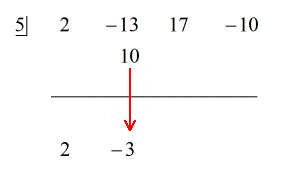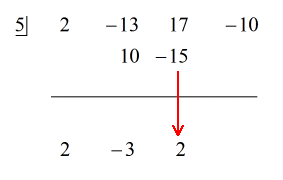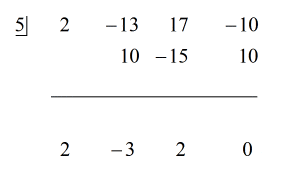
Da resten er lig med nul, betyder det, at divisoren x – 5 er en faktor af dividend
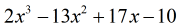
Derfor
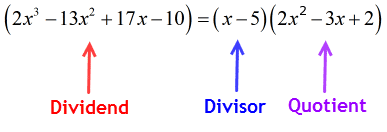
Øvelser med regneark
Du er måske også interesseret i:
Tilføjelse og subtraktion af polynomier
Division af polynomier ved hjælp af den lange divisionsmetode
Multiplikation af binomier ved hjælp af FOIL-metoden
Multiplikation af polynomier




