De coëfficiënten van lineaire regressie interpreteren

Leer hoe u de resultaten van lineaire regressie correct interpreteert – inclusief gevallen met transformaties van variabelen
Nu is er een overvloed aan machine learning-algoritmen die we kunnen uitproberen om de beste fit voor ons specifieke probleem te vinden. Sommige algoritmen hebben een duidelijke interpretatie, andere werken als een blackbox en we kunnen benaderingen zoals LIME of SHAP gebruiken om enkele interpretaties af te leiden.
In dit artikel wil ik me richten op de interpretatie van coëfficiënten van het meest elementaire regressiemodel, namelijk lineaire regressie, met inbegrip van de situaties waarin afhankelijke/onafhankelijke variabelen zijn getransformeerd (in dit geval heb ik het over log-transformatie).
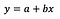
Ik ga ervan uit dat de lezer bekend is met lineaire regressie (zo niet, dan zijn er veel goede artikelen en Medium posts), dus ik zal me uitsluitend richten op de interpretatie van de coëfficiënten.
De basisformule voor lineaire regressie zie je hierboven (ik heb de residuen met opzet weggelaten, om het eenvoudig en to the point te houden). In de formule staat y voor de afhankelijke variabele en x voor de onafhankelijke variabele. Laten we gemakshalve aannemen dat het om een univariate regressie gaat, maar de principes gelden uiteraard ook voor het multivariate geval.
Om het in perspectief te plaatsen, laten we zeggen dat we na fitting van het model de volgende resultaten krijgen:
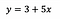
Intercept (a)
Ik zal de interpretatie van het intercept in twee gevallen opsplitsen:
- x is continu en gecentreerd (door het gemiddelde van x van elke waarneming af te trekken, wordt het gemiddelde van getransformeerde x 0) – gemiddelde y is 3 wanneer x gelijk is aan het steekproefgemiddelde
- x is continu, maar niet gecentreerd – gemiddelde y is 3 als x = 0
- x is categorisch – gemiddelde y is 3 als x = 0 (dit keer met aanduiding van een categorie, waarover hieronder meer)
Coefficiënt (b)
- x is een continue variabele
Interpretatie: een toename van x met een eenheid leidt tot een toename van de gemiddelde y met 5 eenheden, waarbij alle andere variabelen constant worden gehouden.
- x is een categorische variabele
Dit vereist een beetje meer uitleg. Laten we zeggen dat x het geslacht beschrijft en waarden kan aannemen (‘man’, ‘vrouw’). Laten we deze variabele nu omzetten in een dummy-variabele die de waarde 0 heeft voor mannen en 1 voor vrouwen.
Interpretatie: de gemiddelde y is 5 eenheden hoger voor vrouwen dan voor mannen, alle andere variabelen constant gehouden.
log-niveaumodel
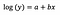
Typisch gebruiken we log-transformatie om buitenwaartse gegevens van een positief scheve verdeling dichter bij de bulk van de gegevens te trekken, om de variabele normaal verdeeld te maken. In het geval van lineaire regressie is een bijkomend voordeel van het gebruik van de log-transformatie de interpreteerbaarheid.
Zoals voorheen geeft de onderstaande formule de coëfficiënten van het aangepaste model weer.
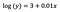
Intercept (a)
De interpretatie is vergelijkbaar met die in het vanillegeval (op niveau), maar voor de interpretatie moeten we de exponent van het intercept nemen exp(3) = 20,09. Het verschil is dat deze waarde staat voor het meetkundig gemiddelde van y (in tegenstelling tot het rekenkundig gemiddelde in het geval van het level-level model).
Coefficiënt (b)
De principes zijn weer gelijk aan die van het level-level model als het gaat om de interpretatie van categorische/numerieke variabelen. Analoog aan het intercept moeten wij de exponent van de coëfficiënt nemen: exp(b) = exp(0,01) = 1,01. Dit betekent dat een eenheidstoename van x een stijging van 1% van de gemiddelde (geometrische) y veroorzaakt, waarbij alle andere variabelen constant worden gehouden.
Twee dingen die hier het vermelden waard zijn:
- Er is een vuistregel als het gaat om de interpretatie van coëfficiënten van zo’n model. Als abs(b) < 0,15 is het vrij veilig om te zeggen dat wanneer b = 0,1 we een toename van 10% in y zullen waarnemen voor een verandering van een eenheid in x. Voor coëfficiënten met een grotere absolute waarde wordt aanbevolen de exponent te berekenen.
- Bij variabelen in een bereik (zoals een percentage) is het voor de interpretatie handiger om de variabele eerst met 100 te vermenigvuldigen en dan het model te passen. Op die manier is de interpretatie intuïtiever, omdat we de variabele met 1 procentpunt verhogen in plaats van met 100 procentpunten (meteen van 0 naar 1).
level-log model
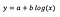
Laten we aannemen dat we na het fitten van het model het volgende krijgen:

De interpretatie van het intercept is dezelfde als in het geval van het level-level model.
Voor de coëfficiënt b geldt dat een toename van x met 1% resulteert in een toename van de gemiddelde y met bij benadering b/100 (0,05 in dit geval), waarbij alle andere variabelen constant worden gehouden. Om het exacte bedrag te krijgen, zouden we b× log(1,01) moeten nemen, wat in dit geval 0,0498 oplevert.
log-log model
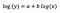
Laten we aannemen dat na fitting van het model we krijgen:
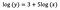
Ook nu richt ik me weer op de interpretatie van b. Een toename van x met 1% leidt tot een toename van de gemiddelde (meetkundige) y met 5%, waarbij alle andere variabelen constant worden gehouden. Om het exacte bedrag te verkrijgen, moeten we
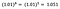
nemen, hetgeen ~5,1% is.
Conclusies
Ik hoop dat dit artikel u een overzicht heeft gegeven van hoe coëfficiënten van lineaire regressie moeten worden geïnterpreteerd, met inbegrip van de gevallen waarin sommige variabelen in log-vorm zijn getransformeerd. Zoals altijd is alle constructieve feedback welkom. Je kunt me bereiken op Twitter of in de comments.




