Beginnende Algebra
Lernziele
- Geordnete Paare darstellen
- Die Bestandteile der Koordinatenebene identifizieren
- Geordnete Paare in der Koordinatenebene darstellen
- Quadranten in der Koordinatenebene identifizieren
- Die vier Quadranten einer Koordinatenebene identifizieren
- Gegeben ein geordnetes Paar, Bestimme seinen Quadranten
Die Koordinatenebene wurde vor Jahrhunderten (genauer gesagt 1637) entwickelt und von dem französischen Mathematiker René Descartes verfeinert. Ihm zu Ehren wird das System manchmal als kartesisches Koordinatensystem bezeichnet. In der Koordinatenebene lassen sich Punkte und Linien grafisch darstellen. Dieses System ermöglicht es uns, algebraische Beziehungen visuell zu beschreiben, und hilft uns auch, algebraische Konzepte zu erstellen und zu interpretieren.
Die Komponenten der Koordinatenebene
Du hast wahrscheinlich schon einmal eine Koordinatenebene benutzt. Haben Sie zum Beispiel schon einmal ein Gitternetz verwendet, um die Position eines Objekts darzustellen? (Das wird auch oft mit Straßenkarten gemacht.)

Diese „Karte“ verwendet ein horizontales und vertikales Gitter, um Informationen über den Standort eines Objekts zu vermitteln. Beachten Sie, dass die Buchstaben A-F am oberen Rand und die Zahlen 1-6 am linken Rand aufgeführt sind. Der allgemeine Standort eines beliebigen Objekts auf dieser Karte kann anhand des Buchstabens und der Nummer des entsprechenden Rasterquadrats ermittelt werden. Zum Beispiel kannst du das Element im Quadrat „4F“ finden, indem du deinen Finger entlang der Horizontalen zum Buchstaben F und dann gerade nach unten bewegst, so dass du in einer Linie mit der 4 bist. Du wirst feststellen, dass sich eine blaue Scheibe an dieser Stelle auf der Karte befindet.
Die Koordinatenebene hat ähnliche Elemente wie das oben gezeigte Gitter. Sie besteht aus einer horizontalen und einer vertikalen Achse, Zahlenlinien, die sich im rechten Winkel schneiden. (Sie stehen senkrecht zueinander.)
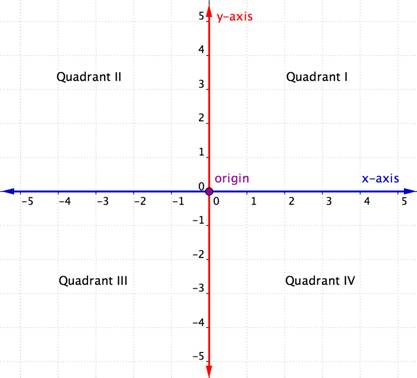
Die horizontale Achse in der Koordinatenebene wird x-Achse genannt. Die vertikale Achse nennt man die y-Achse. Der Punkt, in dem sich die beiden Achsen schneiden, wird als Ursprung bezeichnet. Der Ursprung liegt bei 0 auf der x-Achse und 0 auf der y-Achse.
Orte in der Koordinatenebene werden als geordnete Paare beschrieben. Ein geordnetes Paar gibt die Lage eines Punktes an, indem es die Lage des Punktes entlang der x-Achse (der erste Wert des geordneten Paares) und entlang der y-Achse (der zweite Wert des geordneten Paares) in Beziehung setzt.
In einem geordneten Paar, wie z.B. (x, y), ist der erste Wert die x-Koordinate und der zweite Wert die y-Koordinate. Beachten Sie, dass die x-Koordinate vor der y-Koordinate aufgeführt wird. Da der Ursprung eine x-Koordinate von 0 und eine y-Koordinate von 0 hat, wird sein geordnetes Paar (0, 0) geschrieben.
Betrachten Sie den folgenden Punkt.

Um die Lage dieses Punktes zu bestimmen, beginnen Sie am Ursprung (0, 0) und bewegen sich entlang der x-Achse nach rechts, bis Sie sich unter dem Punkt befinden. Schauen Sie sich die Beschriftung auf der x-Achse an. Die 4 bedeutet, dass Sie sich vom Ursprung aus vier Einheiten nach rechts entlang der x-Achse bewegt haben. Dies ist die x-Koordinate, die erste Zahl des geordneten Paares.
Von der 4 auf der x-Achse gehst du nach oben zum Punkt und achtest auf die Zahl, mit der er auf der y-Achse fluchtet. Die 3 zeigt an, dass du nach Verlassen der x-Achse 3 Einheiten in vertikaler Richtung, also in Richtung der y-Achse, nach oben gegangen bist. Diese Zahl ist die y-Koordinate, die zweite Zahl in dem geordneten Paar. Mit einer x-Koordinate von 4 und einer y-Koordinate von 3 hast du das geordnete Paar (4, 3).
Schauen wir uns ein anderes Beispiel an.
Beispiel
Beschreibe den gezeigten Punkt als geordnetes Paar.

Beschreibe den als geordnetes Paar dargestellten Punkt
Punkte in der Koordinatenebene zeichnen
Nachdem du nun weißt, wie man die x- und y-Achse benutzt, kannst du auch ein geordnetes Paar zeichnen. Denken Sie daran, dass beide Prozesse am Ursprung beginnen – also am Anfang! Das folgende Beispiel zeigt, wie man das geordnete Paar (1,3) grafisch darstellt.
Beispiel
Plotten Sie den Punkt (1, 3).
Im vorherigen Beispiel waren sowohl die x- als auch die y-Koordinate positiv. Wenn eine (oder beide) der Koordinaten eines geordneten Paares negativ sind, müssen Sie sich entlang einer oder beider Achsen in die negative Richtung bewegen. Betrachten Sie das folgende Beispiel, in dem beide Koordinaten negativ sind.
Beispiel
Geben Sie den Punkt (-4,-2) ein.

Die x-Koordinate ist -4, weil sie im geordneten Paar an erster Stelle steht. Beginne am Ursprung und bewege 4 Einheiten in negativer Richtung (links) entlang der x-Achse.
Die y-Koordinate ist -2, weil sie die zweite im geordneten Paar ist. Bewege nun 2 Einheiten in negativer Richtung (nach unten). Wenn du auf die y-Achse schaust, solltest du mit -2 auf dieser Achse ausgerichtet sein.
Die Schritte zum Zeichnen eines Punktes sind unten zusammengefasst.
Schritte zum Zeichnen eines geordneten Paares (x, y) in der Koordinatenebene
- Bestimmen Sie die x-Koordinate. Beginnen Sie am Ursprung und bewegen Sie sich horizontal in Richtung der x-Achse um die durch die x-Koordinate gegebene Strecke. Wenn die x-Koordinate positiv ist, bewege dich nach rechts; wenn die x-Koordinate negativ ist, bewege dich nach links.
- Bestimme die y-Koordinate. Von der x-Koordinate ausgehend, bewege dich vertikal in Richtung der y-Achse um die durch die y-Koordinate angegebene Strecke. Wenn die y-Koordinate positiv ist, bewege dich nach oben; wenn die y-Koordinate negativ ist, bewege dich nach unten.
- Zeichne einen Punkt an der Endposition. Beschrifte den Punkt mit dem geordneten Paar.
Punkte auf der Koordinatenebene aufzeichnen
Bestimme Quadranten und verwende sie zum Aufzeichnen von Punkten
Die sich schneidenden x- und y-Achsen der Koordinatenebene unterteilen sie in vier Abschnitte. Diese vier Abschnitte werden Quadranten genannt. Quadranten werden mit den römischen Ziffern I, II, III und IV benannt, beginnend mit dem oberen rechten Quadranten und gegen den Uhrzeigersinn.
Geordnete Paare innerhalb eines bestimmten Quadranten haben bestimmte Eigenschaften gemeinsam. Sieh dir jeden Quadranten in der folgenden Grafik an. Was fällt dir an den Vorzeichen der x- und y-Koordinaten der Punkte in jedem Quadranten auf?
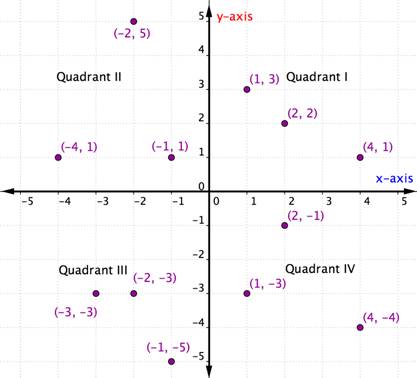
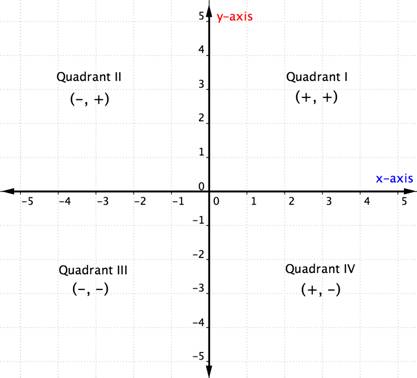
In jedem Quadranten sind die Vorzeichen der x-Koordinaten und y-Koordinaten jedes geordneten Paares gleich. Sie folgen auch einem Muster, das in der folgenden Tabelle dargestellt ist.
| Quadrant | Allgemeine Form des Punktes in diesem Quadranten | Beispiel | Beschreibung |
|---|---|---|---|
| I | (+,+) | (5,4) | Geht ausgehend vom Ursprung entlang der x-Achse in positiver Richtung (rechts) und entlang der y-Achse in positiver Richtung (oben). |
| II | (-,+) | (-5,4) | Ausgehend vom Ursprung, gehe entlang der x-Achse in negativer Richtung (links) und entlang der y-Achse in positiver Richtung (oben). |
| III | (-,-) | (-5,-4) | Ausgehend vom Ursprung, gehe entlang der x-Achse in negativer Richtung (links) und entlang der y-Achse in negativer Richtung (unten). |
| IV | (+,-) | (5,-4) | Ausgehend vom Ursprung gehe entlang der x-Achse in positiver Richtung (rechts) und entlang der y-Achse in negativer Richtung (unten). |
Wenn du die Quadranten in der Koordinatenebene kennst, kannst du den Quadranten eines geordneten Paares bestimmen, ohne es grafisch darzustellen, indem du dir die obige Tabelle ansiehst. Hier ist eine andere Möglichkeit, darüber nachzudenken.
Das folgende Beispiel zeigt, wie man die Quadrantenlage eines Punktes bestimmen kann, indem man einfach über die Vorzeichen seiner Koordinaten nachdenkt. Wenn Sie sich vor dem Einzeichnen eines Punktes Gedanken über die Lage des Quadranten machen, können Sie einen Fehler vermeiden. Es ist auch ein nützliches Wissen, um zu überprüfen, ob man einen Punkt richtig eingezeichnet hat.
Beispiel
In welchem Quadranten liegt der Punkt (-7,10)?
Beispiel
In welchem Quadranten befindet sich der Punkt (-10,-5)?
Was passiert, wenn ein geordnetes Paar eine x- oder y-Koordinate von Null hat? Das folgende Beispiel zeigt den Graphen des geordneten Paares (0,4).
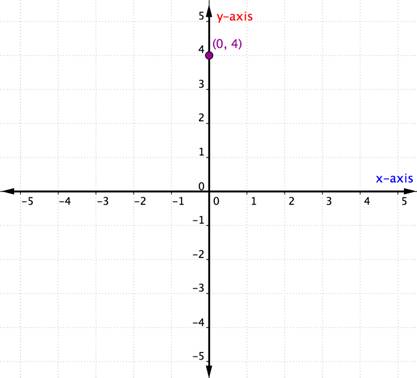
Ein Punkt, der auf einer der Achsen liegt, wird nicht als in einem Quadranten liegend betrachtet. Er liegt einfach auf einer der Achsen. Wenn die x-Koordinate 0 ist, befindet sich der Punkt auf der y-Achse. Gleichermaßen liegt jeder Punkt mit einer y-Koordinate von 0 auf der x-Achse.
Quadranten erkennen und zum Einzeichnen von Punkten verwenden
Zusammenfassung
Die Koordinatenebene ist ein System zur grafischen Darstellung und Beschreibung von Punkten und Linien. Die Koordinatenebene besteht aus einer horizontalen (x-) Achse und einer vertikalen (y-) Achse. Der Schnittpunkt dieser Linien bildet den Ursprung, d. h. den Punkt (0,0). Die Koordinatenebene ist in vier Quadranten unterteilt. Zusammen ermöglichen diese Merkmale des Koordinatensystems die grafische Darstellung und Kommunikation über Punkte, Linien und andere algebraische Konzepte.





