Definition der Wellenfunktion
Fundamentalteilchen, wie z.B. Elektronen, können als Teilchen oder Wellen beschrieben werden.
Elektronen können durch eine Wellenfunktion beschrieben werden, deren Symbol der griechische Buchstabe psi, Ψ oder ψ ist.

Die Wellenfunktion Ψ ist ein mathematischer Ausdruck.Sie trägt entscheidende Informationen über das Elektron, dem sie zugeordnet ist: Aus der Wellenfunktion erhält man die Energie, den Drehimpuls und die Orbitalausrichtung des Elektrons in Form der Quantenzahlen n, l und ml.
Die Wellenfunktion kann ein positives oder negatives Vorzeichen haben, das bei Berechnungen wichtig ist, aber auch, wenn sich die Wellenfunktionen von zwei oder mehr Atomen zu einem Molekül verbinden.
Wellenfunktionen mit gleichem Vorzeichen (phasengleiche Wellen) interferieren konstruktiv, was zu einer möglichen Bindung führt.
Wellenfunktionen mit ungleichen Vorzeichen (phasenverschobene Wellen) interferieren destruktiv.
Im Jahr 1926 leitete Erwin Schrödinger die Wellenfunktion für das einfachste aller Atome, den Wasserstoff, ab.
Die Lösung der Schrödinger-Gleichung ermöglicht es Wissenschaftlern, Wellenfunktionen für Elektronen in Atomen und Molekülen zu bestimmen.
Die Schrödinger-Gleichung ist eine Gleichung der Quantenmechanik: Die berechneten Wellenfunktionen haben diskrete, erlaubte Werte für die in Atomen und Molekülen gebundenen Elektronen; alle anderen Werte sind verboten.
Neben der Bedeutung von Ψ hat auch sein Quadrat Ψ2 eine enorme Bedeutung in der Chemie.
Ψ2 ist die Wahrscheinlichkeitsdichte, die uns sagt, wo das Elektron im Raum um den Kern am wahrscheinlichsten zu finden ist.
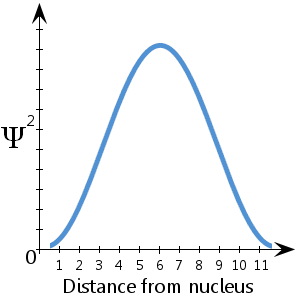
In dem hier dargestellten (fiktiven) Diagramm, das Ψ2 in Abhängigkeit von der Entfernung zum Kern zeigt, sehen wir zum Beispiel, dass das Elektron am wahrscheinlichsten in einem Abstand von etwa 5-7 Einheiten vom Kern zu finden ist.
Es gibt eine 100-prozentige Wahrscheinlichkeit, dass sich das Elektron irgendwo befindet – also eine Wahrscheinlichkeit von 1.
Ψ lässt sich nur für Atome mit einem Elektron, also H, He+, Li2+, Be3+, B4+, C5+ usw., exakt berechnen.
In der mathematischen Sprache sagt man, dass analytische Lösungen für Ψ nur für Ein-Elektronen-Systeme möglich sind.
Ein-Elektronen-Systeme werden oft als hydrierend bezeichnet – das bedeutet „wie Wasserstoff“.“
Für alle anderen Atome, Ionen und Moleküle sind keine analytischen Lösungen für Ψ möglich; es müssen Näherungsmethoden verwendet werden, um es zu berechnen.
Ψ2 und hydrierende Orbitale
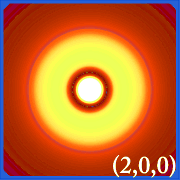
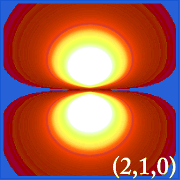
Die Wahrscheinlichkeitsdichte von Wasserstoff (d. h.Die Darstellung der Wahrscheinlichkeitsdichte (d. h. Ψ2) von Wasserstoff für verschiedene Quantenzahlen ermöglicht es, den von den Elektronen besetzten Raum in der Mitte des Kerns darzustellen.Welches Orbital tatsächlich besetzt ist, wird durch die Energiemenge des Elektrons bestimmt.
Beispiele für die Orbitale des Wasserstoffs