Eigenschaften von Vierecken – Rechteck, Quadrat, Parallelogramm, Rhombus, Trapez
In der euklidischen Geometrie ist ein Viereck eine vierseitige 2D-Figur, deren Summe der Innenwinkel 360° beträgt. Das Wort Viereck leitet sich von den beiden lateinischen Wörtern „quadri“ und „latus“ ab, die vier bzw. Seite bedeuten. Daher ist es wichtig, die Eigenschaften von Vierecken zu kennen, um sie von anderen Polygonen zu unterscheiden.
Was sind also die Eigenschaften von Vierecken? Es gibt zwei Eigenschaften von Vierecken:
- Ein Viereck sollte eine geschlossene Form mit 4 Seiten sein
- Alle Innenwinkel eines Vierecks summieren sich zu 360°
In diesem Artikel erhältst du einen Überblick über die 5 Arten von Vierecken und erfährst etwas über die Eigenschaften von Vierecken.
Das wirst du in diesem Artikel lesen:
- Unterschiedliche Typen von Vierecken
- Rechteck
- Eigenschaften von Rechtecken
- Rechteckformeln
- Viereck
- Eigenschaften eines Quadrats
- Formeln von Quadraten
- Parallelogramm
- Eigenschaften von Parallelogrammen
- Parallelogrammformeln
- Rhombus
- Eigenschaften eines Rhombus
- Rhombusformeln
- Trapez/Trapezoid
- Eigenschaften eines Trapezes
- Trapezformeln
- Eigenschaften von Vierecken
- Wichtige Viereckformeln
- Viereckige Fragen
Hier ist ein Video, das die Eigenschaften von Vierecken erklärt:
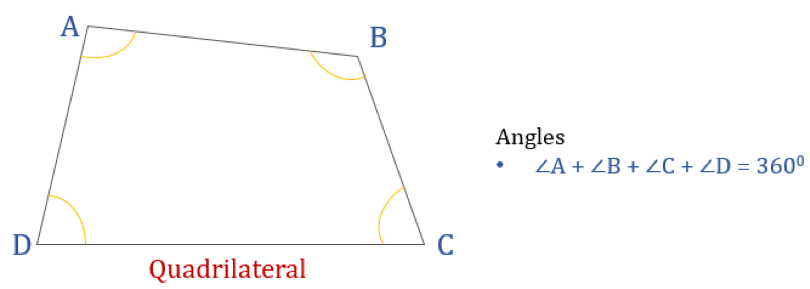
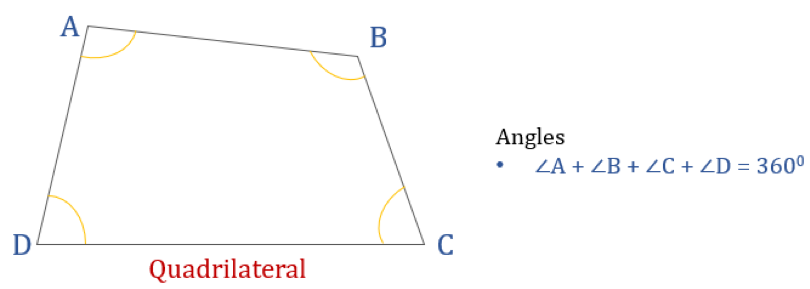
Das unten stehende Diagramm zeigt ein Viereck ABCD und die Summe seiner Innenwinkel. Die Summe aller Innenwinkel beträgt 360°.
Das bedeutet: ∠A + ∠B + ∠C + ∠D = 360°
Unterschiedliche Arten von Vierecken
Es gibt 5 Arten von Vierecken auf der Grundlage ihrer Form. Diese 5 Vierecke sind:
- Rechteck
- Quadrat
- Parallelogramm
- Rhombus
- Trapezium
Lassen Sie uns jedes dieser 5 Vierecke im Detail besprechen:
Hier sind Fragen, die dir zeigen, wie du die Eigenschaften aller 5 Vierecke, die du in diesem Artikel lernst, anwenden kannst.
Rechteck
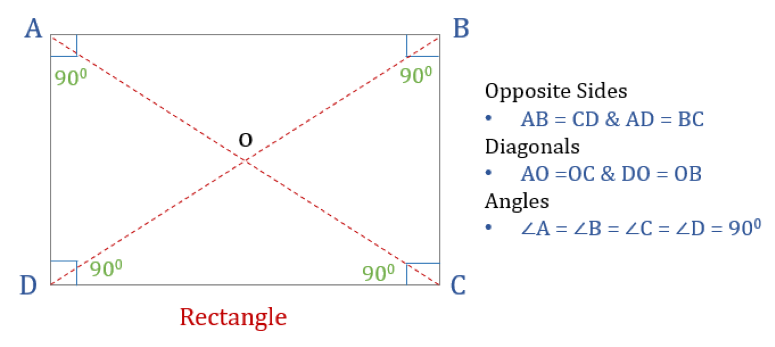
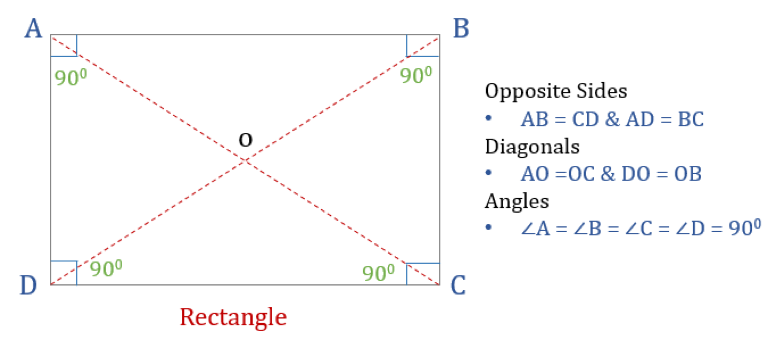
Ein Rechteck ist ein Viereck mit vier rechten Winkeln. Somit sind alle Winkel in einem Rechteck gleich (360°/4 = 90°). Außerdem sind die gegenüberliegenden Seiten eines Rechtecks parallel und gleich, und die Diagonalen halbieren sich gegenseitig.
Eigenschaften von Rechtecken
Ein Rechteck hat drei Eigenschaften:
- Alle Winkel eines Rechtecks sind 90°
- Die gegenüberliegenden Seiten eines Rechtecks sind gleich und parallel
- Die Diagonalen eines Rechtecks halbieren sich
Rechteckformel – Fläche und Umfang eines Rechtecks
Wenn die Länge des Rechtecks L und die Breite B ist, dann,
- Fläche eines Rechtecks = Länge × Breite oder L × B
- Umfang eines Rechtecks = 2 × (L + B)
Diese Übungsfragen helfen dir, die Eigenschaften von Rechtecken zu festigen
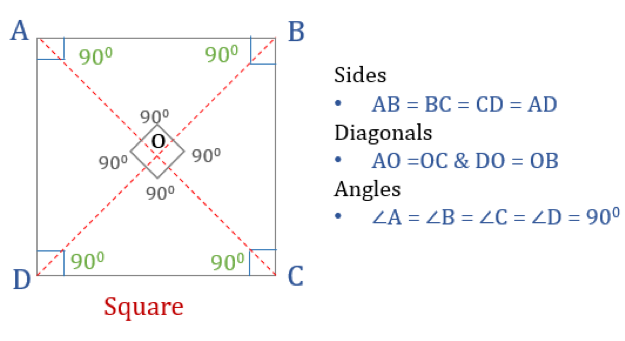
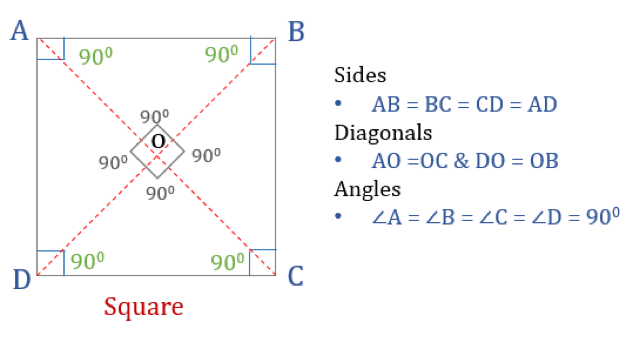
Quadrat
Das Quadrat ist ein Viereck mit vier gleichen Seiten und Winkeln. Es ist auch ein regelmäßiges Viereck, da sowohl seine Seiten als auch seine Winkel gleich sind. Genau wie ein Rechteck hat ein Quadrat vier Winkel von je 90°. Man kann es auch als ein Rechteck betrachten, dessen zwei benachbarte Seiten gleich sind.
Eigenschaften eines Quadrats
Damit ein Viereck ein Quadrat ist, muss es bestimmte Eigenschaften haben. Hier sind die drei Eigenschaften von Vierecken:
- Alle Winkel eines Vierecks sind 90°
- Alle Seiten eines Vierecks sind gleich und parallel zueinander
- Diagonalen halbieren sich senkrecht
Viereckformel – Fläche und Umfang eines Vierecks
Wenn die Seite eines Vierecks ‚a‘ ist, dann,
- Fläche des Quadrats = a × a = a²
- Umfang des Quadrats = 2 × (a + a) = 4a
Diese Übungsfragen helfen Ihnen, die Eigenschaften von Quadraten zu festigen
Wenn Sie die Fragen 50-51 im GMAT bestehen, können Sie ein GMAT-Ergebnis von 700+ erreichen. Bereiten Sie sich mit unseren kostenlosen Vorbereitungsmaterialien auf den GMAT vor und beginnen Sie Ihre Reise zu einem Q50-51 im GMAT. Lernen Sie von Carrie Law, die sich in 3 Wochen von Q35 auf Q50 verbesserte.
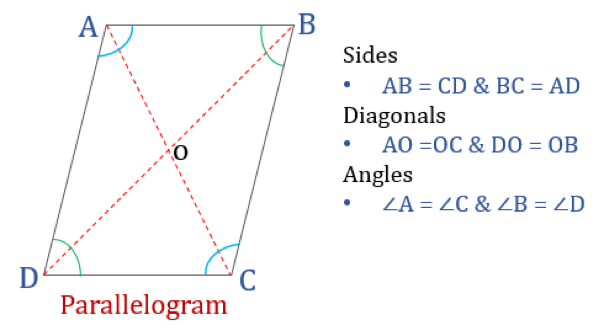
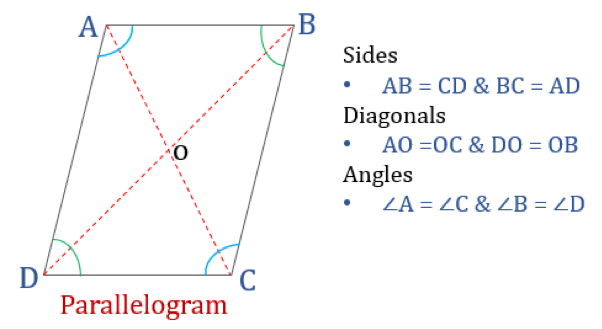
Parallelogramm
Ein Parallelogramm ist, wie der Name schon sagt, ein einfaches Viereck, dessen gegenüberliegende Seiten parallel sind. Es hat also zwei Paare von parallelen Seiten. Außerdem sind die gegenüberliegenden Winkel in einem Parallelogramm gleich und seine Diagonalen halbieren sich gegenseitig.
Eigenschaften des Parallelogramms
Ein Viereck, das die unten genannten Eigenschaften erfüllt, wird als Parallelogramm klassifiziert. Ein Parallelogramm hat vier Eigenschaften:
- Die gegenüberliegenden Winkel sind gleich
- Die gegenüberliegenden Seiten sind gleich und parallel
- Die Diagonalen halbieren sich
- Die Summe zweier beliebiger benachbarter Winkel ist 180°
Parallelogrammformeln – Fläche und Umfang eines Parallelogramms
Wenn die Länge eines Parallelogramms ‚l‘ ist, die Breite ‚b‘ und die Höhe ‚h‘ ist, dann:
- Perimeter des Parallelogramms= 2 × (l + b)
- Fläche des Parallelogramms = l × h
Diese Übungsfragen helfen dir, die die Eigenschaften des Parallelogramms
Rhombus
Ein Rhombus ist ein Viereck, bei dem alle vier Seiten gleich lang sind und die gegenüberliegenden Seiten parallel zueinander sind. Die Winkel sind jedoch nicht gleich 90°. Ein Rhombus mit rechten Winkeln würde zu einem Quadrat werden. Ein anderer Name für die Raute ist „Raute“, da sie der Karo-Farbe in Spielkarten ähnlich sieht.
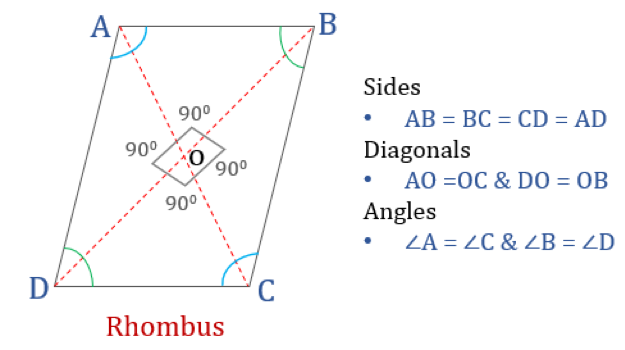
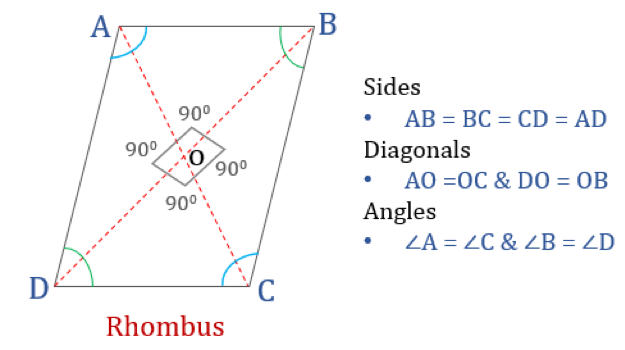
Eigenschaften des Rhombus
Ein Rhombus ist ein Viereck, das die folgenden vier Eigenschaften hat:
- Die gegenüberliegenden Winkel sind gleich
- Alle Seiten sind gleich und, gegenüberliegende Seiten sind parallel zueinander
- Diagonalen halbieren sich senkrecht
- Summe zweier beliebiger benachbarter Winkel ist 180°
Rhombusformeln – Fläche und Umfang eines Rhombus
Wenn die Seite eines Rhombus a ist, dann, Umfang eines Rhombus = 4a
Wenn die Länge der beiden Diagonalen des Rhombus d1 und d2 ist, dann ist der Flächeninhalt eines Rhombus = ½ × d1 × d2
Diese Übungsfragen werden helfen Ihnen, die Eigenschaften der Raute zu festigen
Trapez
Ein Trapez (in den USA Trapezoid genannt) ist ein Viereck, das nur ein Paar parallele Seiten hat. Die parallelen Seiten werden als „Basen“ und die beiden anderen Seiten als „Schenkel“ oder Seitenflächen bezeichnet.
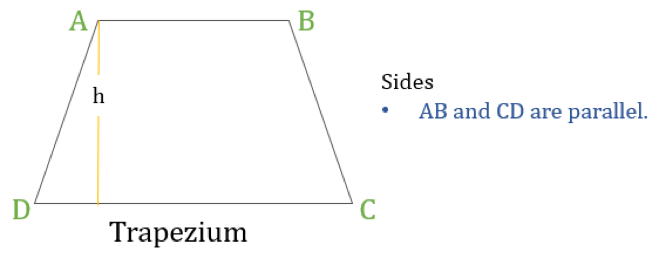
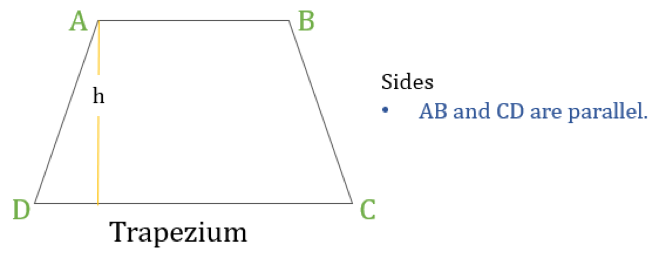
Eigenschaften des Trapezes
Ein Trapez ist ein Viereck, das die folgende eine Eigenschaft hat:
- Nur ein Paar gegenüberliegender Seiten sind parallel zueinander
Trapezformeln – Flächeninhalt und Umfang eines Trapezes
Wenn die Höhe eines Trapezes ‚h‘ ist (wie im obigen Diagramm dargestellt), dann:
- Perimeter des Trapezes= Summe der Längen aller Seiten = AB + BC + CD + DA
- Fläche des Trapezes = ½ × (Summe der Längen der parallelen Seiten) × h = ½ × (AB + CD) × h
Diese Übungsfragen werden dir helfen, die Eigenschaften des Trapezes zu festigen
Eigenschaften der Vierecke
Die folgende Tabelle fasst alle Eigenschaften der Vierecke zusammen, die wir bisher gelernt haben:
| Eigenschaften der Vierecke | Rechteck | Quadrat | Parallelogramm | Rhombus | Trapezium |
| Alle Seiten sind gleich | ✖ | ✔ | ✖ | ✔ | ✖ |
| Gegensätze Die Seiten sind gleich | ✔ | ✔ | ✔ | ✔ | ✖ |
| Opposite Die Seiten sind parallel | ✔ | ✔ | ✔ | ✔ | ✔ |
| Alle Winkel sind gleich | ✔ | ✔ | ✖ | ✖ | ✖ |
| Gegnerische Winkel sind gleich | ✔ | ✔ | ✔ | ✔ | ✖ |
| Summe von zwei benachbarten Winkeln ist 180 | ✔ | ✔ | ✔ | ✔ | ✖ |
| Gegeneinander | ✔ | ✔ | ✔ | ✔ | ✖ |
| Gegeneinander senkrecht | ✖ | ✔ | ✖ | ✔ | ✖ |
Das folgende Bild fasst auch die Eigenschaften von Vierecken zusammen:
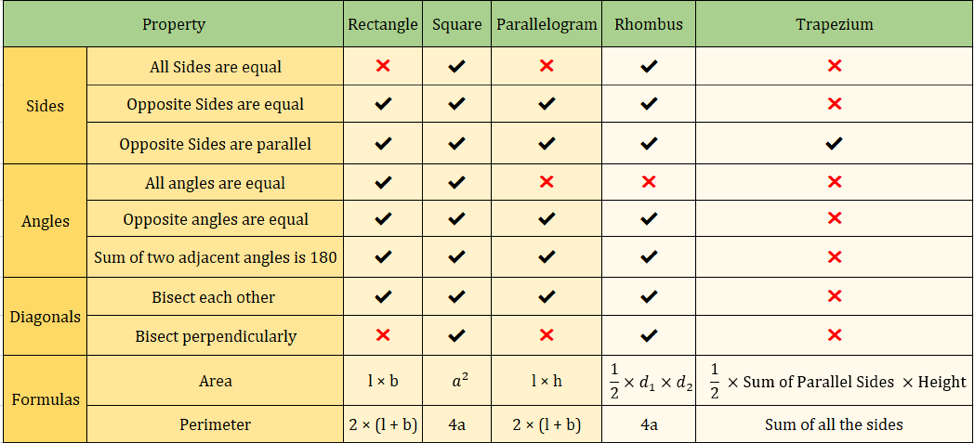
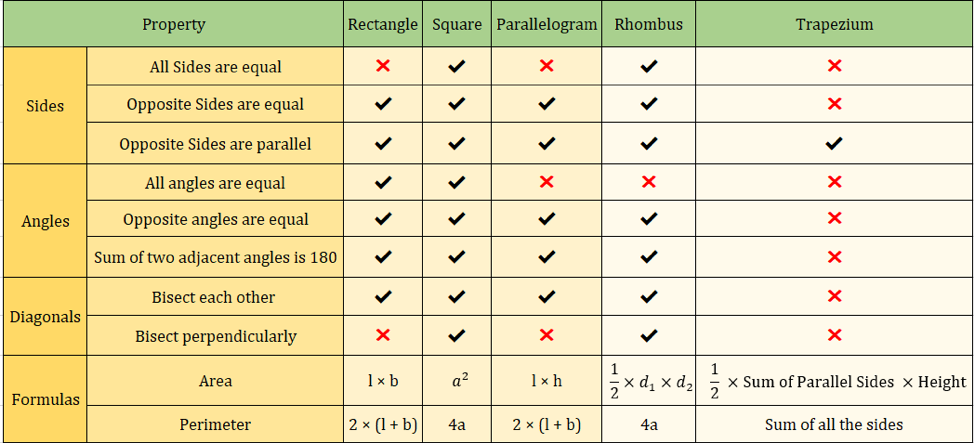
Wichtige Viereckformeln
Die folgende Tabelle fasst die Formeln zu Flächeninhalt und Umfang verschiedener Viereckstypen zusammen:
| Viereckige Formeln | Rechteck | Quadrat | Parallelogramm | Rhombus | Trapezium |
| Fläche | l × b | a² | l × h | ½ × d1 × d2 | ½ × (Summe der parallelen Seiten) × Höhe |
| Perimeter | 2 × (l + b) | 4a | 2 × (l + b) | 4a | Summe aller Seiten |
Weiterlesen:
- Eigenschaften des Kreises | Kreisformeln – Fläche und Umfang
- Eigenschaften der Zahlen – Gerade & Ungerade | Primzahl | HCF & LCM
- Eigenschaften von Dreiecken – Definition | Typen | Klassifikation
- Linien und Winkel – Eigenschaften und ihre Anwendung
Viereckige Fragen
Lassen Sie uns die Anwendung der Eigenschaften von Vierecken anhand der folgenden Beispielfragen üben:
Frage 1
Adam möchte einen Zaun um seinen rechteckigen Garten von 10 m Länge und 15 m Breite bauen. Wie viele Meter Zaun sollte er kaufen, um den gesamten Garten einzuzäunen?
- 20 Meter
- 25 Meter
- 30 Meter
- 40 Meter
- 50 Meter
Lösung
Schritt 1: Gegeben
- Adam hat einen rechteckigen Garten.
- Er hat eine Länge von 10 Metern und eine Breite von 15 Metern.
- Er möchte einen Zaun darum bauen.
Schritt 2: Finde
- die Länge, die benötigt wird, um den Zaun um den gesamten Garten zu bauen.
Schritt 3: Herangehen und Ausrechnen
Der Zaun kann nur um die Außenseiten des Gartens gebaut werden.
- Die benötigte Gesamtlänge des Zauns ist also die Summe der Längen aller Seiten des Gartens.
- Da der Garten rechteckig ist, ist die Summe der Längen aller Seiten nichts anderes als der Umfang des Gartens.
- Perimeter = 2 × (10 + 15) = 50 Meter
Daher ist die erforderliche Länge des Zauns 50 Meter.
Daher ist Option E die richtige Antwort.
Frage: 2
Steve möchte eine rechteckige Wand seines Zimmers streichen. Die Kosten für das Streichen der Wand betragen 1,5 $ pro Quadratmeter. Wenn die Wand 25 Meter lang und 18 Meter breit ist, wie hoch sind dann die Gesamtkosten für das Streichen der Wand?
- $ 300
- $ 350
- $ 450
- $ 600
- $ 675
Lösung
Schritt 1: Gegeben
- Steve möchte eine Wand in seinem Zimmer streichen.
- Die Wand ist 25 Meter lang und 18 Meter breit.
- Die Kosten für das Streichen der Wand betragen 1,5 Dollar pro Quadratmeter.
Schritt 2: Finden
- der Gesamtkosten für das Streichen der Wand.
Schritt 3: Herangehen und Ausarbeiten
- Eine Wand wird auf ihrer gesamten Fläche gestrichen.
- Wenn wir also die Gesamtfläche der Wand in Quadratmetern finden und sie mit den Kosten für den Anstrich von 1 Quadratmeter der Wand multiplizieren, können wir die Gesamtkosten ermitteln.
- Fläche der Wand = Länge × Breite = 25 Meter × 18 Meter = 450 Quadratmeter
- Gesamtkosten für den Anstrich der Wand = 450 × $1.5 = $675
Die richtige Antwort ist also Option E.
Wir hoffen, dass du inzwischen die verschiedenen Arten von Vierecken, ihre Eigenschaften und Formeln kennengelernt hast und weißt, wie du diese Konzepte anwenden kannst, um Fragen zu Vierecken zu lösen. Die Anwendung von Vierecken ist wichtig für die Lösung von Geometriefragen im GMAT. Wenn Sie planen, den GMAT zu absolvieren, können wir Ihnen mit hochwertigem Lernmaterial helfen, auf das Sie kostenlos zugreifen können, indem Sie sich hier registrieren.
Hier sind einige weitere Artikel zum Thema Mathe:
- Verbessern Sie die Genauigkeit bei Mathe-Fragen zu Polygonen
- Geometrie-Fragen – die häufigsten Fehler | GMAT Quant Prep
Wenn Sie planen, den GMAT zu absolvieren, können wir Ihnen Zugang zu hochwertigen Online-Inhalten zur Vorbereitung geben. Wir sind das am besten bewertete GMAT-Vorbereitungsunternehmen auf gmatclub mit mehr als 1950 Bewertungen.
Warum machen Sie nicht einen kostenlosen Test und urteilen Sie selbst?
Schreiben Sie uns an [email protected], wenn Sie Fragen haben.




