Entropie – Die Säule der Thermodynamik und der Informationstheorie
Entropie ist ein vager, aber wirkungsvoller Begriff, der das Rückgrat vieler Schlüsselideen der Thermodynamik und der Informationstheorie bildet. Er wurde erstmals von Physikern im 19. Jahrhundert entdeckt und diente als Leitprinzip für viele revolutionäre Technologien der industriellen Revolution. Der Begriff trug jedoch auch zur Entstehung des Informationszeitalters bei, als er in dem bahnbrechenden Werk A Mathematical Theory of Communication des Mathematikers Claude Shannon auftauchte. Wie kann also ein Begriff für zwei Durchbrüche in verwandten, aber unterschiedlichen Bereichen verantwortlich sein, die etwa ein Jahrhundert auseinander liegen?
Zunächst wollen wir uns ansehen, wie die Entropie in den Naturwissenschaften interpretiert wird. Der erste Hauptsatz der Thermodynamik besagt, dass in einem geschlossenen System Energie weder erzeugt noch zerstört werden kann. Der Zweite Hauptsatz, auch bekannt als Entropiesatz, besagt, dass in einem offenen System die Energie immer von einer höheren Konzentration zu einer niedrigeren Konzentration fließt, um ein thermodynamisches Gleichgewicht zu erreichen. Was bedeutet das in der Praxis? Es bedeutet, dass Ihre Kaffeetasse irgendwann kalt wird und das Eis in Ihrem Getränk mit der Zeit schmilzt, oder dass ein Werkzeug, das ins Feuer gelegt wird, sich erhitzt, wenn die Energie der Flamme auf die Eisenmoleküle übertragen wird, aber abkühlt, sobald es entfernt wird, da sich die Energie in der neuen Umgebung verteilt.

Der Begriff Entropie selbst bezieht sich auf den Zustand der Unordnung in einem bestimmten System. Energie in konzentrierter und nutzbarer Form gilt als geordnet, während Energie in verteilter und nicht verfügbarer Form als ungeordnet gilt.
Entropie bewegt sich nur in eine Richtung – in Richtung Gleichgewicht -, es sei denn, es wirkt eine Kraft von außen auf das System ein, und selbst dann gelingt es äußeren Kräften wie biologischen Systemen nur vorübergehend, den Entropieprozess umzukehren und schließlich aufzugeben (durch Tod). Jede Pflanze und jedes Tier ist ein komplexes Energiesystem, das überlebt, indem es den entropischen Prozess ausgleicht und verfügbare, geordnete Energie aus der Umwelt aufnimmt und dann nährstofffreie Abfälle abgibt. Der Energiedurchsatz in einem lebenden System führt jedoch schließlich zu einem Abbau seiner physischen Struktur, so dass der Organismus zusammenbricht und stirbt (nachdem er hoffentlich sein Endziel, die Fortpflanzung, erreicht hat). Der nicht mehr lebende Energiekörper wird sich zersetzen und sich in die Umgebung auflösen – und das thermodynamische Gleichgewicht wird wiederhergestellt.
Theoretisch wird die Entropie ihren stetigen Marsch erst dann beenden, wenn sie den Wärmetod des Universums herbeigeführt hat – einen Endzustand, in dem es keine freie Energie mehr gibt. Alles auf der Erde und im Weltraum wird sich schließlich ausdehnen, explodieren, sterben und die freie Energie gleichmäßig in dem größten geschlossenen System von allen verteilen: dem Universum. Auf diese Weise ist die Entropie ein universelles Gesetz, das der Schwerkraft ähnelt, da es sowohl im kleinsten als auch im größten Maßstab der Biophysik wirkt.
Wirtschaften sind Organismen, keine Waschmaschinen
Entropie gilt auch für die Wirtschaft. Der Entropieprozess innerhalb eines Organismus, indem er verfügbare Energie aus der Umgebung aufnimmt und in ungeordnete Energie umwandelt, gilt auch für Gruppen von Organismen. Gesellschaften nehmen entropiearme Energiequellen in zwei Formen auf: Vorräte und Ströme. Zu den Vorräten gehören Mineralien seltener Erden, fossile Brennstoffe und andere terrestrische Vorkommen, die durch komplexe, langfristige Erdprozesse über Jahrtausende hinweg entstanden sind. Ströme stammen aus so genannten erneuerbaren Quellen wie Wind, Wasser und Sonnenenergie, zu denen auch Biomasse (als indirekte Erweiterung der Sonnenenergie) gehört. Aufgrund der Natur jeder Quelle sind die Vorräte mengenmäßig begrenzt, während die Ströme sowohl in ihrer Geschwindigkeit als auch in ihrer Menge begrenzt sind. Zivilisationen haben, wie Organismen, einen Stoffwechsel. Sie verarbeiten Energie.

Mit der industriellen Revolution verlagerte sich der primäre Energieinput der Wirtschaft erstmals von Strömen auf terrestrische Vorräte. Pferdegetriebene Pflüge und Windsegel, zwei Formen der Arbeit, die auf Ströme angewiesen sind, wurden durch mechanisierte Landwirtschaft und dampfgetriebene Schiffe ersetzt, die auf fossile Brennstoffe angewiesen sind. Wir nutzten die ruhende, über Millionen von Jahren fossilisierte Sonnenenergie, um die Zivilisation von den Beschränkungen der biologischen Erdströme zu befreien und ein halsbrecherisches Wachstum der Bevölkerung und des BIP zu erreichen.
Trotz der unbestreitbaren wirtschaftlichen und materiellen Vorteile dieses Wandels hatte er den Nebeneffekt, den Entropieprozess zu beschleunigen und die Unordnung im Klimasystem zu vergrößern. Obwohl die Gesamtenergiemenge durch den Wirtschaftsprozess unverändert bleibt (mit Ausnahme der Sonnenenergie), stellt der Abbau von Mineralien und der Verbrauch von fossilen Brennstoffen, die für den Produktionsprozess notwendig sind, eine qualitative Veränderung dar, die die Energie von der Ordnung zur Unordnung bringt. Auf diese Weise bildet die Entropie die Grundlage der Knappheit, denn der Mensch kann Energie nicht in die andere Richtung, von einem Zustand der Unordnung zur Ordnung, bewegen; ohne Entropie wäre es physikalisch möglich, atmosphärisches CO2 wieder in einen Klumpen Kohle zu verwandeln, ebenso wie es möglich wäre, Gummiteilchen, die bei der Zersetzung eines Reifens auf der Fahrbahn verloren gehen, einzufangen und neu zu gestalten.

Am Ende des Tages verbraucht unsere Wirtschaft Dinge und Energie. Auch wenn das Geld, unsere Repräsentation des Wertes, unbegrenzt durch die Wirtschaft kreist, unterliegen die physischen Güter, die es repräsentiert, dem Entropiegesetz. Das derzeitige Wirtschaftssystem ist wie ein Organismus, der unendlich wächst. Unser Herz pumpt unser Blut und hält uns am Leben, aber die Kraft verschleißt mit der Zeit unsere Zellen. Wir altern und bauen ab.
Wie lässt sich die Entropie auf die Datenwissenschaft anwenden?
Nachdem wir uns angesehen haben, wie sich die Entropie auf die Energie bezieht, wollen wir uns nun ansehen, wie sie sich auf die Kommunikation und die Informationstheorie bezieht. Ich denke, dieser Auszug aus Jimmy Sonis und Rob Goodmans Biografie über Claude Shannon, A Mind at Play, ist eine großartige anekdotische Geschichte über die Ursprünge der Entropie:
Shannon trat an den großen Mann mit seiner Idee der Information als aufgelöste Ungewissheit heran – die später im Mittelpunkt seiner Arbeit stehen sollte – und mit einer bescheidenen Frage. Wie sollte er dieses Ding nennen? Von Neumann antwortete sofort: „Sagen wir, dass Information die ‚Entropie‘ reduziert. Zum einen ist das ein gutes, solides physikalisches Wort. Und was noch wichtiger ist“, fuhr er fort, „niemand weiß, was Entropie wirklich ist, also werden Sie in einer Debatte immer im Vorteil sein.“

Bevor wir uns mit Shannons Definition von Entropie befassen, könnte es hilfreich sein, seine Definition von Information zu analysieren. Der Grundgedanke von Shannons Theorie ist, dass der Informationswert einer übermittelten Nachricht davon abhängt, inwieweit der Inhalt der Nachricht überraschend ist. Ein großartiges praktisches Beispiel dafür ist die Häufigkeit von Buchstaben in der Sprache. Wenn das Auftreten eines Buchstabens ein Ereignis ist, dann folgt das wahrscheinlichste Ergebnis jedes gegebenen Ereignisses probabilistisch gesehen dieser Wahrscheinlichkeitsverteilung:
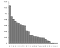
Je mehr Buchstaben es gibt, desto geringer ist die Ungewissheit in der Nachricht. Aber es hängt auch von der Seltenheit der Buchstaben ab. Zum Beispiel, welche der folgenden Botschaften hat mehr Informationsgehalt, 1 oder 2?
_AT
Option „1“ enthält zwei Buchstaben mit relativ hohen Wahrscheinlichkeiten, bei denen man alle möglichen Wörter buchstabieren kann, indem man den fehlenden Buchstaben ausfüllt: „Fledermaus“, „Katze“, „Hut“, „Fett“, „Sat“, usw. Option 2 enthält den vergleichsweise schwer zu fassenden Buchstaben „H“, der einige verbleibende Wortoptionen wie „Hut“ oder „Hit“ bietet, aber nicht so viele wie Option 1. Daher vermittelt Option 2 mehr Informationen, weil sie die Ungewissheit in größerem Maße reduziert.
Wenn also Information aufgelöste Ungewissheit ist, muss Entropie die Ungewissheit sein, die aufgelöst werden muss. Die Seltenheit eines Ereignisses oder seine „Überraschung“ bestimmt seinen Informationsgehalt (wenn Sie jemals Scrabble gespielt haben, wissen Sie, wie begrenzt die Möglichkeiten sind, wenn wir den Buchstaben „Q“ ziehen). Jedes Mal, wenn wir eine Information weitergeben, nimmt die Gesamtentropie, die Unordnung, die Ungewissheit oder wie immer man es nennen will, um einen proportionalen Betrag oder eine proportionale Rate ab. Wie hoch ist dieser proportionale Betrag?
Shannon berechnete, dass das Maß der Informationsentropie, das mit jedem möglichen Datenwert verbunden ist, der negative Logarithmus der Wahrscheinlichkeits-Massenfunktion für den Wert ist:
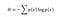
Entropie misst die erwartete Menge an Informationen, die durch die Identifizierung des Ergebnisses eines zufälligen Ereignisses übermittelt wird, wobei die möglichen Ergebnisse eine Wahrscheinlichkeitsfunktion darstellen. Das bedeutet, dass das Werfen eines Würfels eine höhere Entropie hat als das Werfen einer Münze, weil jedes Ergebnis eines Würfelwurfs (⅙) eine geringere Wahrscheinlichkeit hat als Kopf oder Zahl (½). Die Beziehung grafisch zu betrachten hilft:

Durch die Mitteilung eines Ergebnisses von Kopf wissen wir, dass Zahl nicht eingetreten ist.
Im maschinellen Lernen wird die mathematische Interpretation der Entropie zur Berechnung einer Informationsgewinn-Metrik für viele Algorithmen verwendet. Entscheidungsbäume beispielsweise wählen eines von vielen verschiedenen Attributen aus, die auch als Merkmale oder unabhängige Variablen bezeichnet werden, um Stichproben wiederholt in Teilmengen aufzuteilen. Bei jeder Aufteilung wählt der Algorithmus ein Attribut aus, um die Stichprobe aufzuteilen, und fährt damit fort, bis alle Teilmengen rein sind, d. h. jede einzelne Stichprobe in einer Teilmenge denselben Klassifizierungs- oder Zielwert hat.
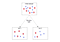
Um die Reinheit einer Stichprobenuntergruppe zu messen, benötigt der Algorithmus ein quantitatives Maß, um objektiv zu entscheiden, nach welchem Merkmal er an jedem gegebenen Knoten aufteilt. An dieser Stelle kommt die Entropie ins Spiel. Bei jedem Schritt berechnet der Algorithmus, welches Attribut den höchsten Informationsgewinn aufweist, und entscheidet dann über die Aufteilung. Er berechnet auch die erwartete Abnahme der Unsicherheit vor und nach der Aufteilung; wenn sie abnimmt, wird die Aufteilung beibehalten und der Algorithmus geht zum nächsten Schritt über. Nimmt sie nicht ab, hat er die Reinheit erreicht und ruht. Auf diese Weise ist er sowohl für die Auswahl des zu teilenden Merkmals als auch für das Anhalten des Prozesses verantwortlich.
Gibt es eine Verbindung zwischen Thermodynamik und Informationstheorie?
Entropie fließt unaufhaltsam durch einen Entscheidungsbaum, so wie sie unaufhaltsam durch eine Tasse Kaffee in die Luft fließt. In der Thermodynamik marschiert sie zum thermodynamischen Gleichgewicht; in der Informationstheorie marschiert sie zur Reinheit.
In ihrem Kern konvergieren die energetische Interpretation der Entropie und die informationstheoretische Interpretation der Entropie am selben Punkt – den fundamentalen Gesetzen der Physik. Kommunikation erfordert Energie, und die Nutzung von Energie erfordert Kommunikation. Nach Shannon stellt der Entropiewert einer Information eine absolute Grenze für die kürzestmögliche durchschnittliche Länge einer Nachricht dar bzw. dafür, wie stark sie komprimiert werden kann, ohne dass bei der Übertragung Informationen verloren gehen. Halbleiter, Taschenlampen und das Klopfen auf eine Pfanne im Morsecode erfordern menschliche Energie, und unsere Kommunikation wird immer nach der effizientesten Art der Übertragung streben.
Im Bereich der Energie versuchen wir, die Entropie zu minimieren, indem wir begrenzen, wie viel wir verbrauchen und wie effizient wir es verbrauchen. Unser Ziel ist es, geordnete Energiequellen zu finden und dem Einfluss der Entropie auf unseren Körper zu widerstehen. In der Kommunikation minimieren wir die Entropie, indem wir Informationen finden und die Unsicherheit verringern. In gewisser Weise können wir den entropischen Prozess der Energie aufhalten, indem wir die Unordnung durch Kommunikation verringern. Ein Jäger und Sammler kann sich mit Hilfe der Sprache mit einem anderen verständigen, um ihn davor zu warnen, von einem Löwen gefressen zu werden, und so die Ungewissheit darüber verringern, 1. wo sich der Löwe aufhält (Informationsentropie) und 2. den Prozess, von einem Löwen gefressen zu werden (Energieentropie). Dieser Akt der Kommunikation reduziert den Wahrscheinlichkeitsraum aller möglichen Ereignisse und ermöglicht es uns, effizienter und effektiver zu handeln. Zu verstehen, wie dieses mächtige Gesetz in der digitalen und physischen Welt funktioniert, ist der Schlüssel zum Verständnis der Zusammenhänge zwischen Thermodynamik und Informationszeitalter.




