Berechnung des erwarteten Geldwerts | Einfache Beispiele

Dezember 25, 2021

admin 0 Comments Articles

Erwarteter Geldwert

Die Analyse des erwarteten Geldwerts (EMV) ist eine statistische Technik im Risikomanagement, die zur Quantifizierung der Risiken verwendet wird. Diese Technik hilft bei der Bestimmung der erforderlichen Gesamtreserve für Unvorhergesehenes. Diese Reserve für unvorhergesehene Ereignisse wird dann in einen vollständigen Projektplan aufgenommen.

Risiken können in Chancen und Bedrohungen unterteilt werden. Chancen werden als positive Risikowerte ausgedrückt, während Bedrohungen als negative Risikowerte ausgedrückt werden. Für die Risikobewertung ist eine risikoneutrale Annahme erforderlich, um Chancen und Bedrohungen richtig einschätzen zu können.

Wir verwenden hier zwei Begriffe.

Wahrscheinlichkeit
Auswirkung

Zunächst müssen wir diese Begriffe verstehen…

Was ist Wahrscheinlichkeit?

Es ist die Wahrscheinlichkeit des Auftretens eines Ereignisses.

Zum Beispiel ist das Ergebnis des Kopfes bei einem Wurf 50% &, so ist 50% das Ende.

Dies erhalten wir, da die Gesamtzahl der Ereignisse 2 ist, und daher ist die Wahrscheinlichkeit für Kopf oder Ende 1/2.

Auf die gleiche Weise, wenn wir einen Würfel werfen, dann ist die Wahrscheinlichkeit für eine Zahl wie eine 3 zu bekommen 1/6, da alle Seiten auf dem Würfel 6 sind. Das ergibt eine Wahrscheinlichkeit von 16,67 % für jede gewürfelte Zahl.

Die Wahrscheinlichkeit ist klar.

Was ist Auswirkung?

Das ist einfach das Geld, das man braucht, um mit dem identifizierten Risiko umzugehen, wenn es eintritt.

Zum Beispiel: Während der Projektdurchführung stellt man fest, dass es einen Ausfall der Ausrüstung geben könnte und man sie durch eine neue ersetzen muss. Die Kosten für die neue Ausrüstung betragen 5000 $. Dies ist der Auswirkungswert.

Es kann eine Kostenauswirkung oder eine Auswirkung auf den Zeitplan sein (Zeit ist Geld).

Wie wird der EMV berechnet?

Der erwartete monetäre Wert für ein Projekt wird berechnet, indem die Wahrscheinlichkeit, dass jedes Ergebnis eintritt, mit dem Wert jedes möglichen Ergebnisses & seiner Auswirkung multipliziert wird:
EMV = P x I
P = Wahrscheinlichkeit, dass jedes Ergebnis eintritt.

I = Wert jedes möglichen Ergebnisses

Einfaches Beispiel;

Ich werde versuchen, dieses Konzept anhand eines grundlegenden Beispiels zu erklären;

Schritt – 1: Holen Sie sich alle Aktivitäten/Aufgaben, Ressourcenkosten aus dem Leistungsverzeichnis (BOQ)

Schritt – 2: Analysieren Sie alle Risikofaktoren im Zusammenhang mit dem Projekt

Schritt – 3: Ermitteln Sie die Wahrscheinlichkeit aller Risiken. Chancen & Bedrohungen

Schritt – 4: Berechnen Sie die Notfallreserve für alle identifizierten Risiken

Schritt – 5: Fassen Sie alles zusammen, und Sie sind fertig

Lassen Sie uns in der folgenden Tabelle sehen; wir haben 5 Risiken identifiziert. Risiko 2 & 3 sind die Chancen, die wir nutzen müssen, damit sie eintreten, und die anderen drei sind Bedrohungen, die wir abmildern, vermeiden oder übertragen müssen.

Risiko	Wahrscheinlichkeit	Auswirkung ($)	EVM (P*I)
1	13%	-10,000	-1300
2	10%	20,000	2,000
3	25%	25,000	6,250
4	15%	-2,50,000	-37,500
5	80%	-1,500	-1200
		-2,16,500	-31,750

Wir haben eine Zahl für die Auswirkung von -216500, aber das ist nicht das, was wir zurückstellen müssen, da wir das EMV berechnen werden, und das ist -31750.

Diesen Betrag müssen wir als Reserve vorhalten.

Ich hoffe, dass Ihnen das jetzt klar ist.

Wahrscheinlichkeit & Auswirkungsmatrix

Wie oben erläutert, ist dies eines der wichtigsten Instrumente der quantitativen Risikoanalyse. Ihr Hauptzweck ist es, letztendlich Geld in der Cost Baseline (dem Budget) – d.h. der Contingency Reserve – zuzuweisen, um das Risiko abzudecken. Zu diesem Zweck werden die qualitativen Auswirkungsskalen der P-I-Matrix in tatsächliche Kosten für jedes Risiko umgewandelt, das im vorangegangenen Prozess als hoch prioritär eingestuft wurde.

Wenn beispielsweise die Auswirkungsbewertung von 0,40 für das Risiko in der nachstehenden Matrix eine „Kostensteigerung von 20 – 40 %“ bedeutet und die geschätzten Gesamtkosten für die vom Eintreten dieses Risikos am stärksten betroffenen Aktivitäten 20.000 $ betragen, dann liegt die „Auswirkung“ in monetärer Hinsicht zwischen 4.000 und 8.000 $ oder im Durchschnitt bei 6.000 $.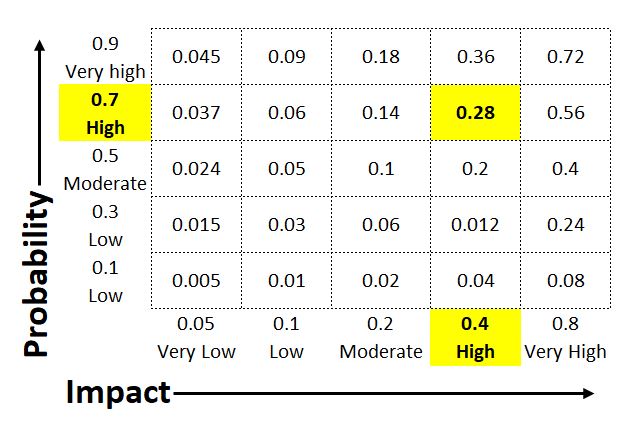

Dieser Wert von 6.000 $ würde dann mit der Wahrscheinlichkeit des Eintretens des Risikos unter Verwendung der Gleichung für den erwarteten Geldwert multipliziert werden:

EMV = P x I
EMV = 0.7 x $6.000 = $4.200

Entscheidungsbaum

EMV wird häufig mit Entscheidungsbäumen verwendet und erfordert ein Verständnis des Konzepts des Erwartungswerts oder des erwarteten Geldwerts ─ ein Konzept, das dem der Exposition ähnelt.
Stellen Sie sich zum Beispiel vor, Sie kaufen ein Gewinnspiel-Los für $1,00. Es gibt zwei mögliche Preise: $100,00 und $10. 00

5% der Lose zahlen $100 aus.
0% zahlen $10 aus.
Die restlichen 97,5% zahlen nichts aus!

Preiswert	Gewinnwahrscheinlichkeit	Durchschnittsgewinn
$ 100,00	0.005	$ 0.50
$ 10.00	0.02	$ 0.20
$ 0	0.975	$ 0
Gesamt	1.000	$ 0.70

Das durchschnittliche Ergebnis für jede einzelne Wette ist im oben genannten Beispiel $0.70. Dieses durchschnittliche Ergebnis wird als Erwartungswert bezeichnet.
Wir können den Erwartungswert niemals mit einer einzigen Wette gewinnen, aber wenn wir die Chance viele Male wiederholen, würden wir im Durchschnitt $0,70 für jeden eingesetzten $1,00 erhalten.

Es gibt viele gute Dinge über diese Technik, wie sie uns gibt;

Das durchschnittliche Ergebnis aller identifizierten Risiken.
Kontingenzreserve.
Die Grundlage für Make-or-Buy-Entscheidungen.
Die Grundlage für Entscheidungen im Hinblick auf die historischen Daten.

Diese Verfahren weisen jedoch auch einige Mängel auf, z.B.

Sie sind nur für größere Projekte geeignet und können daher nicht für kleine Projekte verwendet werden.
Sie stützen sich stark auf historische Daten und Expertenmeinungen, so dass persönliche Vorlieben und Abneigungen das Gesamtergebnis des Projekts beeinflussen können.
Unkorrekte historische Daten werden sich letztendlich auf das Projekt auswirken.
Weniger Informationen über die Anzahl der Risiken werden letztendlich zu einer höheren Auswirkung einzelner Risiken führen, die möglicherweise nicht korrekt sind.

Zusammenfassung

Die Risikoanalyse eines Projekts kann nicht abgeschlossen werden, ohne einen gewissen Betrag als Sicherheitsreserve einzuplanen. Als Projektmanager fühlt man sich immer sicher, wenn man eine bessere Risikoanalyse und einige Reserven in der Hand hat.