Flächeninhalt eines Zylinders – Erklärung und Beispiele
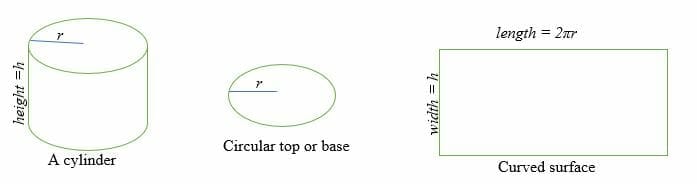
Bevor wir uns mit dem Flächeninhalt eines Zylinders befassen, sollten wir uns einen Überblick über einen Zylinder verschaffen. In der Geometrie ist ein Zylinder eine dreidimensionale Figur mit zwei zueinander parallelen Kreisflächen und einer gekrümmten Oberfläche.
Wie findet man den Flächeninhalt eines Zylinders?
Der Flächeninhalt eines Zylinders ist die Summe aus zwei parallelen und kongruenten Kreisflächen und dem gekrümmten Flächeninhalt.
In diesem Artikel wird erörtert, wie man die Gesamtoberfläche und die Seitenfläche eines Zylinders findet.
Um die Oberfläche eines Zylinders zu berechnen, muss man die Grundfläche (B) und die gekrümmte Oberfläche (CSA) finden. Der Flächeninhalt oder die Gesamtoberfläche eines Zylinders ist also gleich der Summe der Grundfläche mal zwei und der Fläche der gekrümmten Oberfläche.
Die gekrümmte Oberfläche eines Zylinders ist gleich einem Rechteck, dessen Länge 2πr und dessen Breite h ist.
Wobei r = Radius der Kreisfläche und h = Höhe des Zylinders.
Der Flächeninhalt der gekrümmten Fläche = Flächeninhalt eines Rechtecks =l x w = πdh
Die Grundfläche, B = Flächeninhalt eines Kreises = πr2
Die Formel für den Flächeninhalt eines Zylinders
Die Formel für den gesamten Flächeninhalt eines Zylinders lautet:
Gesamtoberfläche eines Zylinders = 2πr2 + 2πrh
TSA = 2πr2 + 2πrh
Wobei 2πr2 die Fläche der oberen und unteren Kreisfläche und 2πrh die Fläche der gekrümmten Fläche ist.
Wenn wir 2πr als gemeinsamen Faktor von RHS nehmen, erhalten wir;
TSA = 2πr (h + r) ……………………………………. (Formel für den Flächeninhalt eines Zylinders)
Lösen wir nun Beispielaufgaben, die den Flächeninhalt eines Zylinders betreffen.
Beispiel 1
Bestimme die Gesamtfläche eines Zylinders mit einem Radius von 5 cm und einer Höhe von 7 cm.
Lösung
Nach der Formel,
TSA = 2πr (h + r)
= 2 x 3.14 x 5(7 + 5)
= 31,4 x 12
= 376,8 cm2
Beispiel 2
Bestimmen Sie den Radius eines Zylinders, dessen Gesamtoberfläche 2136,56 Quadratfuß beträgt, und die Höhe ist 3 Fuß.
Lösung
Gibt:
TSA = 2136.56 Quadratfuß
Höhe, h = 3 Fuß
Aber, TSA = 2πr (h + r)
2136.56 =2 x 3.14 x r (3 + r)
2136.56 = 6.28r (3 + r)
Durch die Distributiv-Eigenschaft der Multiplikation auf der rechten Seite haben wir,
2136.56 = 18.84r + 6.28r2
Dividieren Sie jeden Term durch 6.28
340.22 = 3r + r2
r2 + 3r – 340.22 = 0 ……… (eine quadratische Gleichung)
Wenn man die Gleichung mit der quadratischen Formel löst, erhält man,
r = 17
Der Radius des Zylinders ist also 17 Fuß.
Beispiel 3
Die Kosten für den Anstrich eines zylindrischen Behälters betragen 0,04 $ pro cm2. Ermitteln Sie die Kosten für den Anstrich von 20 Behältern mit einem Radius von 50 cm und einer Höhe von 80 cm.
Lösung
Berechnen Sie die Gesamtoberfläche der 20 Behälter.
TSA = 2πr (h + r)
= 2 x 3.14 x 50 (80 + 50)
= 314 x 130
= 40820 cm2
Die Gesamtoberfläche von 20 Containern = 40.820 cm2 x 20
=816.400 cm2
Die Kosten für den Anstrich = 816.400 cm2 x $0.04 pro cm2
= $32.656,
Die Kosten für den Anstrich von 20 Containern betragen also $32.656,
Beispiel 4
Ermitteln Sie die Höhe eines Zylinders, wenn seine Gesamtoberfläche 2552 in2 und der Radius 14 in beträgt.
Lösung
Gibt:
TSA = 2552 in2
Radius, r = 14 in.
Aber, TSA = 2πr (h + r)
2552 = 2 x 3.14 x 14 (14 + h)
2552 = 87,92(14 + h)
Dividieren Sie beide Seiten durch 87,92 und Sie erhalten,
29.026 = 14 + h
Subtrahieren Sie auf beiden Seiten von 14.
h = 15
Die Höhe des Zylinders beträgt also 15 Zoll.
Seitenfläche eines Zylinders
Wie bereits erwähnt, wird die Fläche der gekrümmten Oberfläche eines Zylinders als Seitenfläche bezeichnet. Einfach ausgedrückt ist die Mantelfläche eines Zylinders die Fläche eines Zylinders ohne die Fläche der Grundfläche und des Bodens (Kreisfläche).
Die Formel gibt die Mantelfläche eines Zylinders an;
LSA = 2πrh
Beispiel 5
Bestimme die Mantelfläche eines Zylinders mit einem Durchmesser von 56 cm und einer Höhe von 20 cm.
Lösung
Gegeben:
Durchmesser = 56 cm, also Radius, r =56/2 = 28 cm
Höhe, h = 20 cm
Nach der Formel,
LSA = 2πrh
= 2 x 3.14 x 28 x 20
= 3516,8 cm2.
Die Mantelfläche des Zylinders beträgt also 3516,8 cm2.
Beispiel 6
Die Mantelfläche eines Zylinders beträgt 144 ft2. Wenn der Radius des Zylinders 7 ft beträgt, finden Sie die Höhe des Zylinders.
Lösung
Gibt;
LSA = 144 ft2
Radius, r = 7 ft




