Interpretieren der Koeffizienten der linearen Regression

Lernen Sie, wie man die Ergebnisse der linearen Regression richtig interpretiert – einschließlich der Fälle mit Transformationen der Variablen
Heutzutage gibt es eine Fülle von Algorithmen für maschinelles Lernen, die wir ausprobieren können, um die beste Lösung für unser spezielles Problem zu finden. Einige der Algorithmen haben eine klare Interpretation, andere arbeiten als Blackbox und wir können Ansätze wie LIME oder SHAP verwenden, um einige Interpretationen abzuleiten.
In diesem Artikel möchte ich mich auf die Interpretation der Koeffizienten des grundlegendsten Regressionsmodells, nämlich der linearen Regression, konzentrieren, einschließlich der Situationen, in denen abhängige/unabhängige Variablen transformiert wurden (in diesem Fall spreche ich von der Log-Transformation).
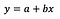
Ich gehe davon aus, dass der Leser mit der linearen Regression vertraut ist (falls nicht, gibt es eine Menge guter Artikel und Beiträge auf Medium), daher werde ich mich ausschließlich auf die Interpretation der Koeffizienten konzentrieren.
Die Grundformel der linearen Regression ist oben zu sehen (ich habe die Residuen absichtlich weggelassen, um die Dinge einfach und auf den Punkt zu bringen). In der Formel steht y für die abhängige Variable und x für die unabhängige Variable. Der Einfachheit halber nehmen wir an, dass es sich um eine univariate Regression handelt, aber die Prinzipien gelten natürlich auch für den multivariaten Fall.
Zur Veranschaulichung sei gesagt, dass wir nach der Anpassung des Modells erhalten:
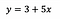
Abschnitt (a)
Ich werde die Interpretation des Abschnitts in zwei Fälle aufteilen:
- x ist kontinuierlich und zentriert (durch Subtraktion des Mittelwerts von x von jeder Beobachtung wird der Durchschnitt des transformierten x 0) – der Durchschnitt y ist 3, wenn x gleich dem Stichprobenmittelwert ist
- x ist kontinuierlich, aber nicht zentriert – der Durchschnitt y ist 3, wenn x = 0
- x ist kategorisch – der Durchschnitt y ist 3, wenn x = 0 (diesmal als Hinweis auf eine Kategorie, mehr dazu unten)
Koeffizient (b)
- x ist eine kontinuierliche Variable
Interpretation: Eine Erhöhung von x um eine Einheit führt zu einer Erhöhung des Durchschnittswertes von y um 5 Einheiten, wenn alle anderen Variablen konstant gehalten werden.
- x ist eine kategoriale Variable
Dies erfordert ein wenig mehr Erklärung. Nehmen wir an, dass x das Geschlecht beschreibt und Werte annehmen kann („männlich“, „weiblich“). Nun wandeln wir es in eine Dummy-Variable um, die für Männer den Wert 0 und für Frauen den Wert 1 annimmt.
Interpretation: Das durchschnittliche y ist für Frauen um 5 Einheiten höher als für Männer, alle anderen Variablen bleiben konstant.
Log-Modell
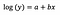
Typischerweise verwenden wir die Log-Transformation, um ausreißende Daten aus einer positiv schiefen Verteilung näher an den Großteil der Daten heranzuziehen, um die Variable normalverteilt zu machen. Bei der linearen Regression ist ein zusätzlicher Vorteil der Log-Transformation die Interpretierbarkeit.
Wie zuvor stellt die folgende Formel die Koeffizienten des angepassten Modells dar.
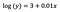
Intercept (a)
Die Interpretation ist ähnlich wie im Vanilla-Fall (Level-Level), allerdings müssen wir zur Interpretation den Exponenten des Intercepts nehmen exp(3) = 20,09. Der Unterschied besteht darin, dass dieser Wert für das geometrische Mittel von y steht (im Gegensatz zum arithmetischen Mittel im Falle des Stufenmodells).
Koeffizient (b)
Die Prinzipien sind wieder ähnlich wie beim Stufenmodell, wenn es um die Interpretation von kategorialen/numerischen Variablen geht. Analog zum Achsenabschnitt müssen wir den Exponenten des Koeffizienten nehmen: exp(b) = exp(0,01) = 1,01. Das bedeutet, dass ein Anstieg von x um eine Einheit einen Anstieg von 1 % des durchschnittlichen (geometrischen) y verursacht, wenn alle anderen Variablen konstant gehalten werden.
Zwei Dinge sind hier erwähnenswert:
- Es gibt eine Faustregel, wenn es um die Interpretation von Koeffizienten eines solchen Modells geht. Wenn abs(b) < 0,15 ist, kann man mit ziemlicher Sicherheit sagen, dass bei b = 0,1 ein Anstieg von y um 10 % bei einer Änderung von x um eine Einheit zu beobachten ist. Bei Koeffizienten mit größerem Absolutwert empfiehlt es sich, den Exponenten zu berechnen.
- Bei Variablen, die in einem bestimmten Bereich liegen (z. B. ein Prozentsatz), ist es für die Interpretation bequemer, die Variable zunächst mit 100 zu multiplizieren und dann das Modell anzupassen. Auf diese Weise ist die Interpretation intuitiver, da wir die Variable um 1 Prozentpunkt statt um 100 Prozentpunkte (von 0 auf 1 sofort) erhöhen.
Level-Log-Modell
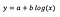
Nehmen wir an, dass wir nach Anpassung des Modells erhalten:

Die Interpretation des Achsenabschnitts ist die gleiche wie im Fall des Stufenmodells.
Für den Koeffizienten b gilt: Ein Anstieg von x um 1 % führt zu einem ungefähren Anstieg des durchschnittlichen y um b/100 (in diesem Fall 0,05), wenn alle anderen Variablen konstant gehalten werden. Um den genauen Betrag zu erhalten, müsste man b× log(1,01) nehmen, was in diesem Fall 0,0498 ergibt.
log-log-Modell
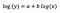
Nehmen wir an, dass wir nach Anpassung des Modells erhalten:
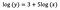
Noch einmal konzentriere ich mich auf die Interpretation von b. Eine Erhöhung von x um 1 % führt zu einer Erhöhung des durchschnittlichen (geometrischen) y um 5 %, wenn alle anderen Variablen konstant gehalten werden. Um den genauen Betrag zu erhalten, müssen wir
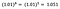
nehmen, was ~5,1% entspricht.
Schlussfolgerungen
Ich hoffe, dieser Artikel hat Ihnen einen Überblick über die Interpretation von Koeffizienten der linearen Regression gegeben, einschließlich der Fälle, in denen einige der Variablen log-transformiert wurden. Wie immer ist jedes konstruktive Feedback willkommen. Sie können mich auf Twitter oder in den Kommentaren erreichen.




