Synthetische Divisionsmethode
Ich muss sagen, dass die synthetische Division die „spaßigste“ Methode ist, Polynome zu dividieren. Im Vergleich zur langen Polynomdivisionsmethode sind weniger Schritte nötig, um die Antwort zu erhalten. In dieser Lektion werde ich fünf (5) Beispiele durchgehen, die dich hoffentlich mit den grundlegenden Verfahren zur erfolgreichen Division von Polynomen mit Hilfe der synthetischen Division vertraut machen.
Das ist zu beachten:
- Vergewissere dich, dass die Dividende in Standardform ist. Das bedeutet, dass die Potenzen in abnehmender Reihenfolge stehen.
- Der Divisor muss die Form x – \links( c \rechts) haben.
Beispiele für die Division von Polynomen mit der synthetischen Division
Beispiel 1: Teile das folgende Polynom.
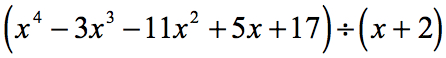
Lassen Sie uns das gegebene Problem noch einmal betrachten und gegebenenfalls die notwendigen Anpassungen vornehmen.
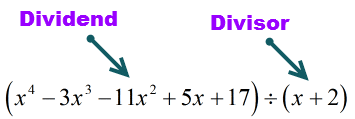
Der Dividend (der zu teilende Stoff) ist in der Standardform, weil die Exponenten in abnehmender Reihenfolge stehen. Das ist gut!
Der Divisor muss umgeschrieben werden als
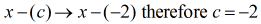
An dieser Stelle kann ich nun die synthetische Division aufstellen, indem ich die Koeffizienten des Dividenden extrahiere und sie dann oben aneinanderreihe.
Direkt auf der linken Seite wird der Wert von c = – 2 in den „Kasten“ gesetzt.
Schließlich wird eine horizontale Linie direkt unter den Koeffizienten des Dividenden konstruiert.
Schritte:
1. Lass den ersten Koeffizienten unter die horizontale Linie fallen.
2. Multipliziere die Zahl, die du fallen gelassen hast, mit der Zahl im „Kasten“. Was auch immer das Produkt ist, setze es über die horizontale Linie direkt unter den zweiten Koeffizienten.
3. Addiere die Zahlenspalte und setze dann die Summe direkt unter die horizontale Linie.
4. Wiederhole den Vorgang, bis du keine Spalten mehr zum Addieren hast.
Siehe die animierte Lösung unten:
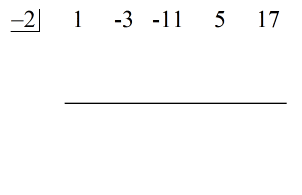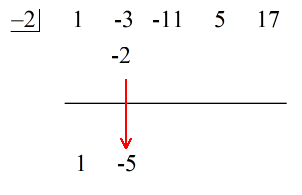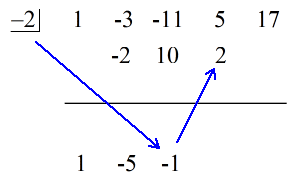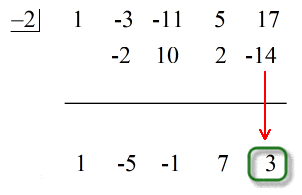
Die letzte Zahl unter der horizontalen Linie ist immer der Rest! Der Rest dieser Aufgabe ist 3.
Wie stellen wir also unsere endgültige Antwort dar?
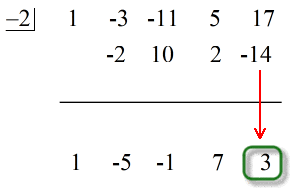
- Zeige deine endgültige Antwort in der Form
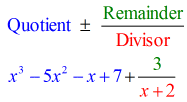
Beachte, dass die Zahlen unter der horizontalen Linie außer der letzten (Rest) die Koeffizienten des Quotienten sind.
Mehr noch, die Exponenten der Variablen des Quotienten sind alle um 1 reduziert.
Beispiel 2: Dividiere das Polynom.
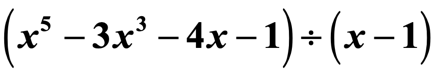
Das ist keine Fangfrage. Beachte, dass der Quotient nicht alle Exponenten der Variablen x enthält.
Ich sehe, dass uns {x^4} und {x^2} fehlen. Um alle Koeffizienten der Variablen x in abnehmender Potenz einzubeziehen, sollten wir das ursprüngliche Problem wie folgt umschreiben. Fügen Sie an die fehlenden x Nullen an. Drücke auch den Divisor als x – (c) aus, was den Wert von c klar erkennen lässt, nämlich c = + 1.
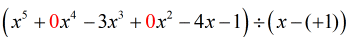
Von diesem Punkt aus kann ich nun die Zahlen aufstellen, um mit dem Prozess fortzufahren.
Schritte:
1. Setze den ersten Koeffizienten unter die horizontale Linie.
2. Multipliziere die Zahl, die du fallen gelassen hast, mit der Zahl in der „Box“. Das Produkt wird oberhalb der horizontalen Linie direkt unter dem zweiten Koeffizienten platziert.
3. Addiere die Zahlenspalte und setze die Summe direkt unter die horizontale Linie.
4. Wiederhole den Vorgang, bis du keine Spalten mehr zum Addieren hast.
Siehe die animierte Lösung unten:
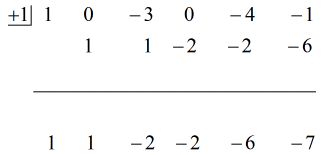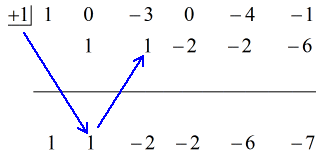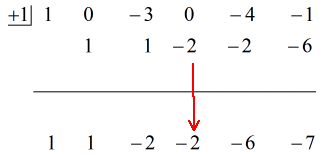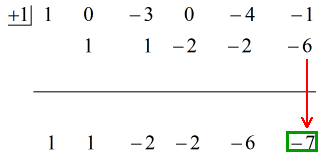
Die endgültige Antwort in der Form
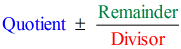
wir haben
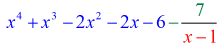
Beispiel 3: Teile das folgende Polynom.
\left( { – 2{x^4} + x} \right) \div \left( {x – 3} \right)
Das wird immer interessanter! Der Quotient sieht auf jeden Fall furchtbar aus, denn es fehlt eine Menge. Es fehlen nicht nur einige x, nämlich {x^3} und {x^2}, sondern auch die Konstante ist weg.
Um dies zu beheben, werde ich das ursprüngliche Problem so umschreiben, dass alle x berücksichtigt werden. Aber was noch wichtiger ist, vergiss nicht, die fehlende Konstante, die Null ist, mit einzubeziehen.
Das „neue und verbesserte“ Problem sollte wie folgt aussehen:
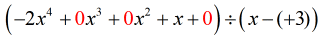
Von hier aus kannst du mit den Schritten wie gewohnt fortfahren.
Schritte:
1. Ziehe den ersten Koeffizienten unter die horizontale Linie.
2. Multipliziere die Zahl, die du gezogen hast, mit der Zahl in der „Box“. Das Produkt wird oberhalb der horizontalen Linie direkt unter dem zweiten Koeffizienten platziert.
3. Addiere die Zahlenspalte und setze die Summe direkt unter die horizontale Linie.
4. Wiederhole den Vorgang, bis du keine Spalten mehr zum Addieren hast.
Sieh dir die animierte Lösung unten an:
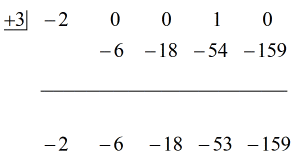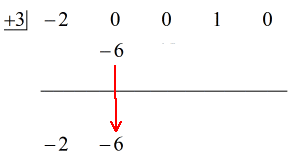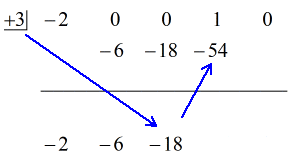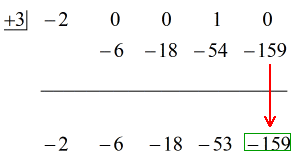
Okay, die endgültige Antwort lautet
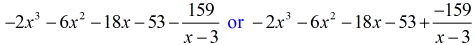
Die endgültige Antwort kannst du auf zwei Arten schreiben. Die erste Möglichkeit ist die Verwendung des Minus- oder Subtraktionssymbols, um anzuzeigen, dass der Rest negativ ist. Die zweite Möglichkeit ist die Verwendung des +-Symbols, wobei man ein negatives Symbol an den Zähler anhängt. Sie bedeuten dasselbe!
Beispiel 4: Teilen Sie das folgende Polynom.
\left( { – {x^5} + 1} \right) \div \left( {x + 1} \right)
Lassen Sie sich von diesem Problem nicht entmutigen. Es ist eigentlich ganz einfach, vor allem jetzt, wo du schon ein paar Beispiele durchgenommen hast. Denke immer daran, „die fehlenden Teile zu ergänzen“, richtig?
Betrachte die Dividende und du solltest zustimmen, dass die fehlenden Teile {x^4}, {x^3}, {x^2} und x sind.
Wenn wir das ursprüngliche Problem, das zur synthetischen Division geeignet ist, neu schreiben, erhalten wir…
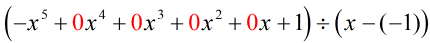
Wir haben die fehlenden x mit Nullen aufgefüllt und lösen explizit für c = -1.
Schritte:
1. Ziehe den ersten Koeffizienten unter die horizontale Linie.
2. Multipliziere die Zahl, die du gezogen hast, mit der Zahl in der „Box“. Das Produkt wird oberhalb der horizontalen Linie direkt unter dem zweiten Koeffizienten platziert.
3. Addiere die Zahlenspalte und setze die Summe direkt unter die horizontale Linie.
4. Wiederhole den Vorgang, bis du keine Spalten mehr zum Addieren hast.
Siehe die animierte Lösung unten:
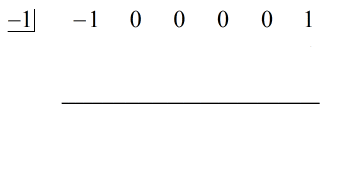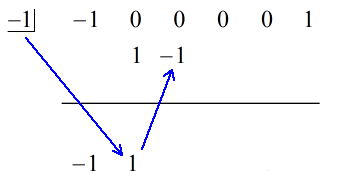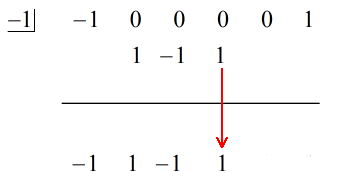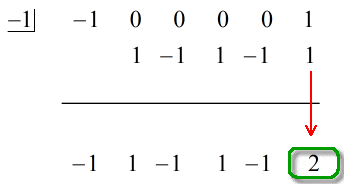
Die letzte Zahl unter der horizontalen Linie wird immer der Rest sein. Vergiss das nicht. In diesem Fall ist der Rest gleich 2.
Unsere endgültige Antwort ist
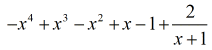
Beispiel 5: Dividiere das Polynom durch ein Binom.
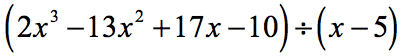
In diesem Beispiel erhalten wir einen Rest von Null. Wenn das passiert, wird der Divisor zu einem Faktor des Dividenden. Mit anderen Worten, der Divisor teilt den Dividend gleichmäßig.
Bei der Untersuchung der Aufgabe sehe ich, dass keine Komponenten fehlen. Alle Potenzen von x sind berücksichtigt, und wir haben eine Konstante. Das ist großartig! Dieses Problem ist tatsächlich zur synthetischen Division geeignet.
Schritte:
1. Ziehe den ersten Koeffizienten unter die horizontale Linie.
2. Multipliziere die Zahl, die du gezogen hast, mit der Zahl im „Kasten“. Das Produkt wird oberhalb der horizontalen Linie direkt unter dem zweiten Koeffizienten platziert.
3. Addiere die Zahlenspalte und setze die Summe direkt unter die horizontale Linie.
4. Wiederhole den Vorgang, bis du keine Spalten mehr zum Addieren hast.
Siehe unten die animierte Lösung:
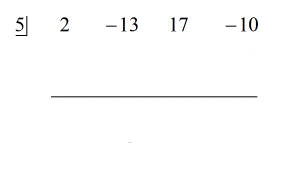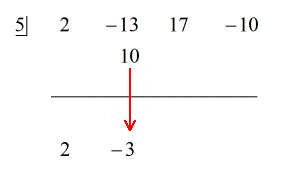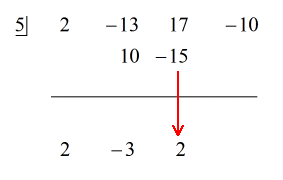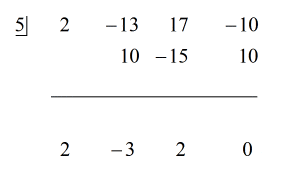
Da der Rest gleich Null ist, bedeutet dies, dass der Divisor x – 5 ein Faktor des Dividenden ist
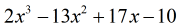
daher
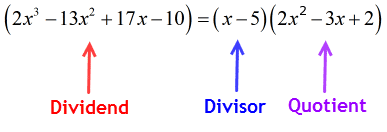
Üben mit Arbeitsblättern
Das könnte dich auch interessieren:
Addieren und Subtrahieren von Polynomen
Dividieren von Polynomen mit der Methode der langen Division
Multiplizieren von Binomischen mit der FOIL-Methode
Multiplizieren von Polynomen




