Zwei Arten der Division von Brüchen und einige Beispiele
In diesem Beitrag werden wir lernen, wie man Brüche dividiert. Dazu schauen wir uns zwei verschiedene Methoden an:
Methode 1 zur Division von Brüchen: Kreuzmultiplikation
- Diese Methode besteht darin, den Zähler des ersten Bruches mit dem Nenner des zweiten Bruches zu multiplizieren und dann die Antwort in den Zähler des resultierenden Bruches zu schreiben.
- Nächstens multiplizieren wir den Nenner des ersten Bruches mit dem Zähler des zweiten Bruches und schreiben dann die Antwort in den Nenner des resultierenden Bruches*.
- Schließlich vereinfachen wir den endgültigen Bruch.
Um zum Beispiel den Bruch
![]()
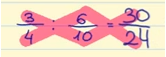
zu teilen, multiplizieren wir den Zähler des ersten Bruchs (3) mit dem Nenner des zweiten Bruchs (10). So erhalten wir den Zähler des letzten Bruches: 3 x 10 = 30.
Als Nächstes multiplizieren wir den Nenner des ersten Bruchs (4) mit dem Zähler des zweiten Bruchs (6). So erhalten wir den Nenner des letzten Bruches: 4 x 6 = 24.
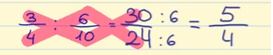
Der letzte Schritt besteht darin, den Bruch zu vereinfachen. Da beide Zahlen Vielfache von 6 sind, können wir Zähler und Nenner durch 6 dividieren.
30 ÷ 6 = 5
24 ÷ 6 = 4
Das Ergebnis der Division ist also 5/4.
Methode 2 der Division von Brüchen: Invertieren und Multiplizieren
- Schritt 1: Invertiere den zweiten Bruch. Das heißt, du vertauschst den Zähler mit dem Nenner.
- Schritt 2: Vereinfache einen beliebigen Zähler mit einem beliebigen Nenner.
- Schritt 3: Multipliziere quer.
Zum Beispiel wollen wir dividieren:

Schritt 1: Wir kehren den zweiten Bruch 6/4 um. Daraus wird 4/6.
Schritt 2: Wir vereinfachen die Zähler mit den Nennern.
Die Zähler sind:
12 = 2 x 2 x 3
4 = 2 × 2
Die Nenner sind:
5 = 5
6 = 2 × 3
Wir können sowohl vom Zähler als auch vom Nenner eine 2 und eine 3 vereinfachen. Wir nennen dieses Verfahren „Kreuzaufhebung“, wenn ein Zähler einen gemeinsamen Faktor mit dem anderen Nenner hat.
Und wir multiplizieren quer:
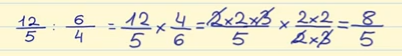
Wir hoffen, dass dir dieser Beitrag gefallen hat.
Wenn du mehr Beispiele sehen möchtest, besuche unseren früheren Beitrag über Wortprobleme mit Bruchteilung und Wie man Brüche vereinfacht: Lowest Terms Fractions.
Wenn du noch viel mehr Mathe lernen willst, melde dich bei Smartick an.
Weiter lernen:
- Lernen und üben, wie man Brüche subtrahiert oder addiert
- Lernen und üben, wie man Brüche multipliziert
- Lernen, wie man Brüche mit zwei verschiedenen Methoden dividiert
- Lernen, wie man subtrahiert Brüche
- Brüche addieren üben mit Beispielen



- Autor
- Aktuelle Beiträge
Ein multidisziplinäres und multikulturelles Team, das sich aus Mathematikern, Lehrern, Professoren und anderen Bildungsexperten zusammensetzt!
Sie bemühen sich, die bestmöglichen mathematischen Inhalte zu erstellen.
- Beispiele für Mathe-Wortaufgaben der 3. Klasse mit Lösungen – 25.03.2021
- Konsekutive Innenwinkel: Was sie sind und wie man sie findet mit Beispielen – 03/11/2021
- Beispiele für Wortprobleme der zweiten Klasse mit Lösungen – 02/04/2021




