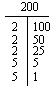Getallen in hun priemgetal

admin 0 Comments Articles

Getallen in hun priemgetal

Alle gehele getallen worden gecategoriseerd als ofwel priemgetal ofwel samengesteld getal, met uitzondering van nul en één, die speciale gevallen zijn. Laten we eens kijken naar het verschil tussen priemgetallen en samengestelde getallen. Priemgetallen hebben precies twee factoren, één en het getal zelf. Als je de deelbaarheidsregels kent (behandeld in het volgende onderdeel), dan is het bepalen van de priemgetallen van 1-100 een relatief gemakkelijke taak. Hier zijn de priemgetallen tot 25:

2, 3, 5, 7, 11, 13, 17, 19, 23

Er is geen patroon voor het vinden van alle priemgetallen die er bestaan, hoewel wiskundigen priemgetallen hebben gevonden met bijna acht miljoen cijfers. Dit is een van de resterende grote wiskundige mysteries voor wiskundigen.

Samengestelde getallen hebben meer dan twee factoren, maar niet een oneindig aantal factoren. Alle even getallen (behalve het getal twee) zijn samengesteld, omdat ze allemaal door twee gedeeld kunnen worden.

Nul is priem noch samengesteld. Daar elk getal maal nul gelijk is aan nul, zijn er oneindig veel factoren voor een product van nul. Een samengesteld getal moet een eindig aantal factoren hebben.

Een is ook priem noch samengesteld. De enige manier om een product van één te krijgen is door 1 te vermenigvuldigen met 1. Maar dubbele factoren worden maar één keer geteld, dus heeft één maar één factor. (Een priemgetal heeft precies twee factoren, dus kan één geen priemgetal zijn.)

Een typische testvraag is welk getal uit een lijst priem is (of samengesteld of geen van beide).

Probeer deze eens:

Vraag

Welk van de volgende is een priemgetal?

1. 33
2. 45
3. 41
4. 51

Ontdek antwoord

Het juiste antwoord is C. Eenenveertig is een priemgetal; de andere getallen zijn samengesteld. Wees voorzichtig met 51-het komt van 3 x 17.

Coole regels

Gelijkbaarheidsregels zijn hulpmiddelen om je te helpen minder te delen. De deelbaarheidsregels kunnen je helpen om te bepalen of een getal priem of samengesteld is en om samengestelde getallen op te splitsen in hun priemfactoren, het onderwerp dat we hierna zullen behandelen.

Deelbaarheidsregels zijn sneltoetsen om je te vertellen of een getal deelbaar is door een ander getal. De regels behandelen de deling door de getallen 2-10 en laten je toe getallen tot 100 te controleren. Klik op de getallen in de grafiek.

Vraag

Welk van de volgende getallen is niet deelbaar door 3?

1. 4.873
2. 7.521
3. 12.642
4. 25.308

Het juiste antwoord is A. De snelle manier om dit probleem op te lossen is door de deelbaarheidsregel te gebruiken; tel de cijfers van elk getal bij elkaar op en zoek het getal dat geen veelvoud van drie is. De langzame manier zou zijn om elk delingsprobleem te doen – zelfs op een rekenmachine zal deze methode langer duren!

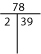
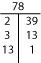
Prime Factorization: T’s en Tree

Dit is nog een onderwerp waar je sinds de middelbare school misschien niet meer aan gedacht hebt. De Fundamentele Stelling van de Rekenkunde stelt dat elk samengesteld getal kan worden opgesplitst in een uniek product van priemgetallen.

Prime factorization is het proces dat de priemgetalproducten van een gegeven samengesteld getal vindt. Priemfactorisatie is nuttig op zichzelf, maar veel van de toepassingen ervan hebben betrekking op breuken, die we verderop zullen behandelen.

Je kunt misschien de priemfactorisatie van een getal in je hoofd vinden. Bijvoorbeeld, 12 is 2 x 2 x 3 of 22 x 3. (Priemfactorisaties worden vaak voorgesteld met exponenten.)

Als u de priemfactorisatie niet mentaal kunt vinden, probeer dan ofwel een Factor-T of een Factorboom.

Factor-T

In een Factor-T hebt u twee kolommen: de linkerkolom met de priemgetallen en de rechterkolom met progressief kleinere quotiënten van deling.

Stap 1: Bepaal een priemgetal dat deelt in uw gegeven getal. Schrijf dat getal in de linkerkolom.

Stap 2: Schrijf het quotiënt van uw getal gedeeld door het priemgetal in de rechterkolom.

Stap 3: Zoek nu een priemgetal dat deelt in het quotiënt, 39 in dit geval. Ga door met stap 1 en 2 totdat je een één hebt in de rechterkolom. De getallen aan de linkerkant zijn uw priemfactorisatie! De priemfactorisering van 78 is 2 x 3 x 13. Geen enkel ander getal heeft deze priemfactorisatie.

Hier is nog een voorbeeld voor de priemfactorisatie van 200.

De priemfactorisatie van 200 is 23 x 52.

Factorboom

Met een factorboom breekt u een getal steeds op in het product van twee getallen totdat de getallen priem zijn. Er zijn vele tactieken om aan de top van de boom te beginnen, wat betekent dat de bomen er niet noodzakelijk hetzelfde zullen uitzien als ze door verschillende mensen worden gemaakt. Gebruik wat voor u het beste werkt om twee getallen te vinden die samen kunnen vermenigvuldigen tot het getal dat u nodig hebt.

Hier volgt nog een voorbeeld voor de priemfactorisatie van 200.

Review

• Priemgetallen hebben precies twee factoren, één en zichzelf.
• Samengestelde getallen hebben meer dan twee factoren, maar geen oneindig aantal.
• Nul en één zijn noch priem, noch samengesteld.
• Deelbaarheidsregels zijn sneltoetsen die je kunnen helpen bij het bepalen van factoren van een getal.
• Elk samengesteld getal kan geschreven worden als een uniek product van priemgetallen, dat de priemfactorisatie van een getal wordt genoemd.
• Twee handige methoden om priemfactorisaties te vinden zijn factor-T’s en factorbomen.