Definition of Wave Function
Le particelle fondamentali, come gli elettroni, possono essere descritte come particelle o onde.
Gli elettroni possono essere descritti usando una funzione d’onda, il cui simbolo è la lettera greca psi, Ψ o ψ.

La funzione d’onda Ψ è un’espressione matematica.Trasporta informazioni cruciali sull’elettrone a cui è associata: dalla funzione d’onda otteniamo l’energia, il momento angolare e l’orientamento orbitale dell’elettrone sotto forma di numeri quantici n, l e ml.
La funzione d’onda può avere un segno positivo o negativo.Il segno è importante nei calcoli.È anche importante quando le funzioni d’onda di due o più atomi si uniscono per formare una molecola.
Funzioni d’onda con segni simili (onde in fase) interferiranno costruttivamente, portando alla possibilità di legame.Funzioni d’onda con segni non uguali (onde fuori fase) interferiranno distruttivamente.
Nel 1926, Erwin Schrödinger dedusse la funzione d’onda per il più semplice di tutti gli atomi, l’idrogeno.Risolvere l’equazione di Schrödinger permette agli scienziati di determinare funzioni d’onda per gli elettroni in atomi e molecole.
L’equazione di Schrödinger è un’equazione della meccanica quantistica: le funzioni d’onda calcolate hanno valori discreti e permessi per gli elettroni legati negli atomi e nelle molecole; tutti gli altri valori sono proibiti.
Oltre all’importanza di Ψ, il suo quadrato Ψ2 ha anche un enorme significato in chimica.
Ψ2 è la densità di probabilità.Essa ci dice dove è più probabile trovare l’elettrone nello spazio intorno al nucleo.
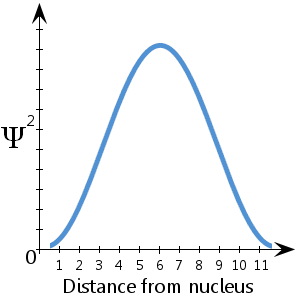
Per esempio, nel diagramma schematico (fittizio) qui tracciato, che mostra Ψ2 contro la distanza dal nucleo, vediamo che l’elettrone è più probabile che si trovi tra circa 5-7 unità dal nucleo.Vediamo anche che c’è una probabilità molto piccola che l’elettrone sia al nucleo o più di circa 11½ unità di distanza dal nucleo.
C’è una probabilità del 100% che l’elettrone sia da qualche parte – in altre parole una probabilità di 1.
Ψ può essere calcolato esattamente solo per gli atomi con un elettrone, cioè H, He+, Li2+, Be3+, B4+, C5+, ecc.”
Per tutti gli altri atomi, ioni e molecole, non sono possibili soluzioni analitiche per Ψ; sono necessari metodi di approssimazione per calcolarlo.
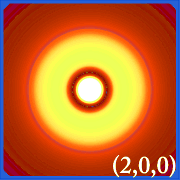
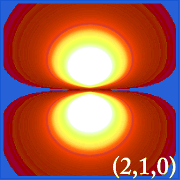
Ψ2 e orbitali idrogenici
Tracciare la densità di probabilità dell’idrogeno (es.Le varie distribuzioni di Ψ2 sono gli orbitali elettronici dell’idrogeno.L’orbitale effettivamente occupato è determinato dalla quantità di energia dell’elettrone.
Esempi di orbitali dell’idrogeno