Entropia – Il pilastro della Termodinamica e della Teoria dell’Informazione
L’entropia è un termine vago ma potente che forma la spina dorsale di molte idee chiave della Termodinamica e della Teoria dell’Informazione. È stato identificato per la prima volta dagli scienziati fisici nel 19° secolo e ha agito come principio guida per molte delle tecnologie rivoluzionarie della Rivoluzione Industriale. Tuttavia, il termine ha anche aiutato a innescare l’Era dell’Informazione quando è apparso nell’opera rivoluzionaria del matematico Claude Shannon, A Mathematical Theory of Communication. Quindi, come può un termine essere responsabile di due scoperte, a circa un secolo di distanza l’una dall’altra, in campi correlati ma disparati?
Prima di tutto, iniziamo da come l’entropia viene interpretata nelle scienze fisiche. La Prima Legge della Termodinamica stabilisce che in qualsiasi sistema chiuso, l’energia non può essere né creata né distrutta. La Seconda Legge, conosciuta anche come Legge dell’Entropia, stabilisce che in un sistema aperto, l’energia passa sempre da una concentrazione più alta ad una più bassa per raggiungere l’equilibrio termodinamico. Cosa significa questo in pratica? Significa che la vostra tazza di caffè alla fine si raffredda e il ghiaccio nella vostra bevanda si scioglie nel tempo, o che un utensile messo nel fuoco si riscalda perché l’energia della fiamma si trasferisce alle molecole di ferro, ma si raffredda una volta che viene rimosso perché l’energia si distribuisce nel nuovo ambiente circostante.

Il termine entropia si riferisce allo stato di disordine in un dato sistema. L’energia in forma concentrata e utilizzabile è considerata ordinata, mentre l’energia in forma distribuita e non disponibile è considerata disordinata.
L’entropia si muove solo in una direzione – verso l’equilibrio – a meno che non sia agita da una forza esterna al sistema, e anche allora, forze esterne come i sistemi biologici riescono solo temporaneamente a invertire il processo di entropia e alla fine cedono (attraverso la morte). Qualsiasi pianta o animale è un sistema energetico complesso che sopravvive compensando il processo entropico e raccogliendo energia disponibile e ordinata dall’ambiente per poi emettere rifiuti privati delle sostanze nutritive. Ma il flusso di energia nel sistema vivente alla fine degrada la sua struttura fisica, facendo sì che l’organismo si rompa e muoia (si spera avendo completato il suo obiettivo finale di riproduzione). Il corpo di energia, non più vivente, si decomporrà e si dissiperà nell’ambiente circostante – e nell’equilibrio termodinamico.
Teoricamente, l’entropia fermerà la sua marcia costante solo quando avrà portato alla morte termica dell’universo – uno stato finale dove non c’è energia libera. Tutto sulla terra e nello spazio alla fine si espanderà, esploderà, morirà e distribuirà uniformemente l’energia libera attraverso quello che è davvero il più grande sistema chiuso di tutti: l’universo. In questo modo, l’entropia è una legge universale simile alla gravità, poiché opera sia alla scala più piccola che a quella più grande della biofisica.
Le economie sono organismi, non lavatrici
L’entropia si applica anche all’economia. Il processo di entropia all’interno di un organismo, acquisendo energia disponibile dall’ambiente circostante e trasformandola in energia disordinata, vale anche per i gruppi di organismi. Le società prendono fonti di energia a bassa entropia in due forme: scorte e flussi. Le scorte includono minerali di terre rare, combustibili fossili e altri depositi terrestri creati da complessi processi terrestri a lungo termine nel corso dei millenni. I flussi provengono da quelle che sono considerate fonti rinnovabili, come il vento, l’acqua e l’energia solare, che includono anche la biomassa (come estensione indiretta dell’energia solare). Data la natura di ogni fonte, le scorte sono limitate nella quantità, mentre i flussi sono limitati sia nel tasso che nella quantità. Le civiltà, come gli organismi, hanno metabolismi. Elaborano energia.

La rivoluzione industriale spostò per la prima volta l’input energetico primario dell’economia dai flussi alle riserve terrestri. Gli aratri trainati dai cavalli e le vele a vento, due forme di lavoro che dipendono dai flussi, sono stati sostituiti dall’agricoltura meccanizzata e dalle navi a vapore, che dipendono dai combustibili fossili. Abbiamo capitalizzato l’energia solare dormiente fossilizzata in milioni di anni per liberare la civiltà dai vincoli dei flussi biologici terrestri e creare una crescita a rotta di collo della popolazione e del PIL.
Nonostante gli innegabili vantaggi economici e materiali di questo cambiamento, ha avuto l’effetto collaterale di accelerare il processo di entropia e aumentare il disordine nel sistema climatico. Anche se la quantità totale di energia rimane invariata attraverso il processo economico (con l’eccezione dell’energia solare), l’estrazione di minerali e il consumo di combustibili fossili necessari per il processo di produzione caratterizza un cambiamento qualitativo che sposta l’energia dall’ordine al disordine. In questo modo, l’entropia è alla base della scarsità perché l’uomo non può spostare l’energia nell’altro senso, da uno stato di disordine a uno di ordine; senza entropia, sarebbe fisicamente possibile ritrasformare il CO2 atmosferico in un grumo di carbone, così come sarebbe possibile catturare e riconfigurare le particelle di gomma perse quando un pneumatico si degrada sul marciapiede.

In fin dei conti, la nostra economia utilizza cose ed energia. Anche se il denaro, la nostra rappresentazione del valore, circola nell’economia indefinitamente, i beni fisici che rappresenta sono soggetti alla legge dell’entropia. L’attuale sistema economico è come un organismo che cresce indefinitamente. Il nostro cuore pompa il nostro sangue e ci tiene in vita, ma la forza consuma le nostre cellule nel tempo. Invecchiamo e ci degradiamo.
Come si applica l’entropia alla scienza dei dati?
Ora che abbiamo visto come l’entropia si riferisce all’energia, vediamo come si applica alla comunicazione e alla teoria dell’informazione. Penso che questo estratto dalla biografia di Claude Shannon di Jimmy Soni e Rob Goodman, A Mind at Play, sia una grande storia aneddotica delle origini dell’entropia:
Shannon avvicinò il grande uomo con la sua idea di informazione come incertezza risolta – che sarebbe diventata il cuore del suo lavoro – e con una domanda senza pretese. Come doveva chiamare questa cosa? Von Neumann rispose subito: “diciamo che l’informazione riduce l'”entropia”. Per prima cosa è una buona e solida parola fisica. E soprattutto”, continuò, “nessuno sa cosa sia realmente l’entropia, quindi in un dibattito sarete sempre in vantaggio.”

Prima di affrontare la definizione di entropia di Shannon, potrebbe essere utile scomporre la sua definizione di informazione. L’idea di base della teoria di Shannon è che il valore informativo di un messaggio comunicato dipende dal grado in cui il contenuto del messaggio è sorprendente. Un grande esempio di questo in pratica è l’uso della frequenza delle lettere nel linguaggio. Probabilisticamente, se l’istanza di una lettera è un evento, allora il risultato più probabile di ogni dato evento segue questa distribuzione di probabilità:
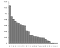
Più lettere ci sono, meno incertezza c’è nel messaggio. Ma dipende anche dalla rarità della lettera. Per esempio, quale dei seguenti messaggi contiene più informazioni, 1 o 2?
_AT
L’opzione “1” include due lettere con una probabilità relativamente alta, dove è possibile comporre ogni sorta di parole riempiendo la lettera mancante: “Bat”, “Cat”, “Hat”, “Fat”, “Sat”, ecc. L’opzione 2 include la lettera “H”, relativamente sfuggente, che ha alcune opzioni di parole rimanenti come “Hat” o “Hit”, ma non così tante come l’opzione 1. Pertanto, l’opzione 2 comunica più informazioni perché riduce l’incertezza in misura maggiore.
Quindi, se l’informazione è incertezza risolta, l’entropia deve essere l’incertezza da risolvere. La rarità di un evento, o la sua “sorpresa”, determina il suo contenuto informativo (se avete mai giocato a Scarabeo, saprete quanto sarebbero limitate le opzioni se estraessimo la lettera “Q”). Ogni volta che comunichiamo un pezzo di informazione, l’entropia complessiva, il disordine, l’incertezza, o come volete chiamarla, diminuisce di una quantità o tasso proporzionale. Cos’è questa quantità proporzionale?
Shannon ha calcolato che la misura dell’entropia dell’informazione associata ad ogni possibile valore dei dati è il logaritmo negativo della funzione di massa della probabilità per il valore:
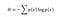
L’entropia misura la quantità attesa di informazione trasmessa identificando il risultato di un evento casuale, dove i possibili risultati sono una funzione di probabilità. Questo implica che il lancio di un dado ha un’entropia più alta del lancio di una moneta, perché ogni risultato del lancio del dado (⅙) ha una probabilità minore rispetto all’uscita di testa o croce (½). Guardare la relazione graficamente aiuta:

Comunicando un risultato di testa, sappiamo che croce non si è verificato.
Nell’apprendimento automatico, l’interpretazione matematica dell’entropia è usata per calcolare una metrica di guadagno di informazioni per molti algoritmi. Gli alberi decisionali, per esempio, selezionano uno dei molti attributi diversi, noti anche come caratteristiche o variabili indipendenti, per dividere ripetutamente i campioni in sottoinsiemi. Ad ogni suddivisione, l’algoritmo seleziona un attributo per dividere il campione, e continua a farlo fino a quando tutti i sottoinsiemi sono puri, o in altre parole, ogni singolo campione in un sottoinsieme condivide la stessa classificazione o valore obiettivo.
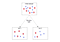
Per misurare la purezza di un sottoinsieme di campioni, l’algoritmo ha bisogno di una misura quantitativa per scegliere oggettivamente su quale caratteristica dividere ad ogni dato nodo. È qui che entra in gioco l’entropia. Ad ogni passo, l’algoritmo calcola quale attributo mostrerà il più alto guadagno di informazione, quindi decide la divisione. Calcola anche la diminuzione prevista dell’incertezza prima e dopo la divisione; se diminuisce, la divisione viene mantenuta e l’algoritmo procede al passo successivo. Se non è diminuita, ha raggiunto la purezza e si ferma. In questo modo, è responsabile sia della selezione di quale caratteristica dividere sia dell’arresto del processo.
C’è un legame tra termodinamica e teoria dell’informazione?
L’entropia scorre inesorabilmente attraverso un albero decisionale proprio come scorre inesorabilmente attraverso una tazza di caffè nell’aria. Nell’energia, marcia verso l’equilibrio termodinamico; nella Teoria dell’Informazione, marcia verso la purezza.
Al suo centro, l’interpretazione energetica dell’entropia e l’interpretazione della teoria dell’informazione dell’entropia convergono allo stesso punto – le leggi fondamentali della fisica. La comunicazione richiede energia, e l’uso dell’energia richiede la comunicazione. Secondo Shannon, il valore di entropia di un’informazione fornisce un limite assoluto alla lunghezza media più breve possibile di un messaggio, o quanto può essere compresso, senza perdere informazioni durante la trasmissione. I semiconduttori, le torce elettriche e il battere su una padella in codice Morse richiedono energia umana, e le nostre comunicazioni cercheranno sempre il mezzo di trasmissione più efficiente.
Nell’energia, cerchiamo di minimizzare l’entropia limitando la quantità che consumiamo e l’efficienza con cui la consumiamo. Il nostro obiettivo è trovare fonti ordinate di energia e resistere all’influenza dell’entropia sui nostri corpi. Nelle comunicazioni, minimizziamo l’entropia trovando informazioni e riducendo l’incertezza. In un certo senso, riducendo il disordine attraverso la comunicazione, possiamo fermare il processo entropico dell’energia; un cacciatore-raccoglitore può usare il linguaggio per comunicare con un altro per avvertire di essere mangiato da un leone, riducendo sia l’incertezza di 1. dove si trova il leone (entropia dell’informazione) sia 2. il processo di essere mangiato da un leone (entropia dell’energia). Questo atto di comunicare riduce lo spazio di probabilità di tutti gli eventi possibili e ci permette di agire in modo più efficiente ed efficace. Comprendere la natura di come questa potente legge opera nel regno digitale e fisico è la chiave per comprendere le connessioni tra la termodinamica e l’era dell’informazione.




