Lessico della pompa centrifuga
Le perdite di carico sono il risultato dell’attrito delle pareti in tutti i tipi di tubazioni e della resistenza locale al flusso, per esempio nelle valvole e nei raccordi (vedi anche Perdita di pressione).
Velocità di flusso consigliate
- Per l’acqua fredda:
Tratto di aspirazione 0.7-1,5 m/s
Linea di scarico 1,0-2,0 m/s - Per acqua calda:
Linea di aspirazione 0,5-1,0 m/s
Linea di scarico 1,5-3,5 m/s
L’equazione per la perdita di carico di un flusso in un tratto rettilineo di tubazione con sezione circolare è:
λ Fattore di attrito del tubo
L Lunghezza del tubo in m
d Diametro interno del tubo in m
v Velocità del flusso in una sezione trasversale in m/s
(= 4 Q / π d2 con Q in m3/s)
g Accelerazione dovuta alla gravità in m/s2
vedi fig. 1 e 4 Perdita di carico
Il fattore di attrito del tubo è stato stabilito sperimentalmente. Dipende solo dallo stato di flusso del fluido trattato e dalla rugosità relativa (d/k) dei tubi attraverso i quali il fluido scorre. Per le sezioni di tubi non circolari si applica il diametro equivalente in termini fluidomeccanici (d):
A Sezione trasversale in m2
U Circonferenza della sezione bagnata in m
(la superficie libera di un canale aperto non è considerata)
Lo stato del flusso è determinato dal numero di Reynolds (Re) secondo le leggi di affinità. Per i tubi circolari vale quanto segue:
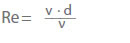
v Velocità del flusso in una sezione trasversale in m/s
(= 4 Q / π d2 con Q in m3/s)
ν Viscosità cinematica in m2/s
(per acqua a 20 °C: 1.00 – 10 – 6 m2/s)
d Diametro interno del tubo in m
Vedi Fig. 4 Perdita di carico
Per tubazioni idraulicamente lisce come quelle in metallo trafilato liscio o in plastica (es. PE o PVC), o in caso di flusso laminare, il fattore di attrito del tubo (λ) può essere calcolato. Per un flusso laminare in un tubo con un numero di Reynolds inferiore a 2320, il fattore di attrito del tubo è indipendente dalla rugosità:
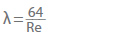
Se il flusso è turbolento, o il numero di Reynolds superiore a 2320, il fattore di attrito del tubo in tubi idraulicamente lisci può essere rappresentato da un’equazione empirica secondo Eck (per il fatto che le deviazioni sono inferiori all’1% se il numero di Reynolds è inferiore a 108).
Il fattore di attrito del tubo (λ) dipende anche da un altro parametro adimensionale, cioè dalla rugosità relativa della superficie interna del tubo (d/k). Entrambi devono essere specificati nella stessa unità (es. mm).
Vedi Fig. 1 Perdita di carico
(k) è la rugosità media assoluta della superficie interna del tubo per la quale sono disponibili valori approssimativi a seconda del materiale e dei processi di fabbricazione. Vedi Fig. 2 Perdita di carico
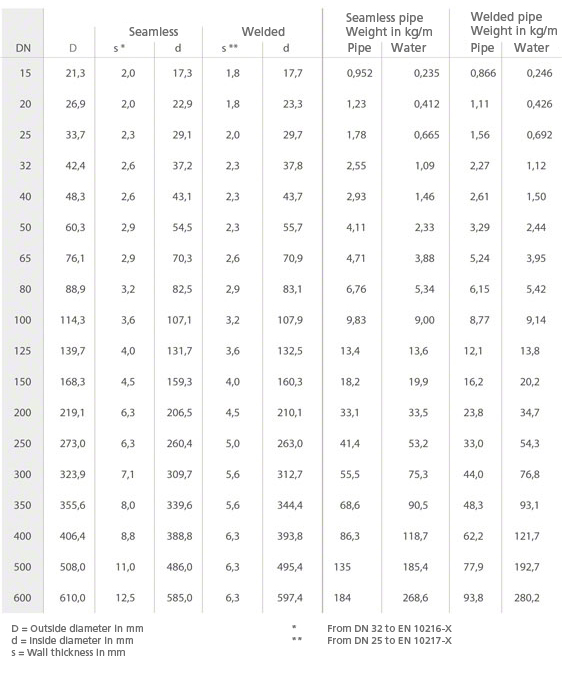Fig. 2 Perdita di carico: Stime delle altezze medie picco-valle k (rugosità assoluta) dei tubi
Al di sopra della curva limite, il fattore di attrito del tubo (λ) dipende solo dalla rugosità relativa del tubo (d/k). Vedi Fig. 1 Perdita di carico
Per questa regione si può usare la seguente equazione empirica di Moody:
Per uso pratico, la perdita di carico (HL) per 100 m di tubo diritto in acciaio è mostrata nel diagramma come funzione della portata (Q) e del diametro interno del tubo (d).
Vedi Fig. 3 Perdita di carico
I valori sono validi solo per acqua fredda e pulita o per fluidi con la stessa viscosità cinematica, per tubi completamente pieni e per una rugosità assoluta della superficie interna del tubo di k = 0.05 mm.
Dimensioni, pesi, riempimento d’acqua per tubi nuovi in acciaio senza saldatura o saldati longitudinalmente
Vedi allegato, Perdita di carico, Fig. 4
L’effetto di un aumento della rugosità superficiale k sarà dimostrato di seguito per una serie di parametri di uso frequente (diametro nominale DN = 50-300, velocità di flusso v = 0,8 a 3,0 m/s). Vedi Fig. 3 Perdita di carico
La regione azzurra corrisponde alla regione marcata in modo simile per una rugosità media assoluta di k = 0,05 mm.
Vedi Fig. 1 Perdita di carico
Per una rugosità aumentata di un fattore 6 (tubo in acciaio vecchio leggermente incrostato con k = 0,30 = 300 μm (0.30 mm), i fattori di attrito del tubo (e le relative perdite di carico proporzionali) nella regione blu scuro sono solo il 25 – 60 % più alti di prima.
Vedi Fig. 1 Perdita di carico
Per i tubi di scarico si deve prendere in considerazione l’aumento della rugosità causato dalla sporcizia. Per i tubi soggetti a incrostazioni estreme, la perdita di carico effettiva può essere determinata solo sperimentalmente. Le deviazioni dal diametro nominale cambiano considerevolmente la perdita di carico, poiché il diametro interno del tubo è presente nell’equazione alla quinta potenza.
Una riduzione del 5 % del diametro interno, per esempio, porta ad un aumento della perdita di carico fino al 30 %. È quindi importante che il diametro interno non venga semplicemente sostituito con il diametro nominale nei calcoli.
Le perdite di carico nei tubi di plastica o nelle tubazioni metalliche trafilate lisce sono molto basse grazie alle superfici lisce dei tubi. Le perdite di carico stabilite sono valide per l’acqua a 10 °C. Ad altre temperature, la perdita per i tubi di plastica deve essere moltiplicata per un fattore di correzione della temperatura specificato per tenere conto della loro maggiore espansione termica. Per le acque di scarico o altre acque non trattate, si deve tenere conto di un’ulteriore perdita di carico del 20-30 % per eventuali depositi.
Perdite di carico per tubi in plastica e in metallo trafilato liscio
Vedi allegato, Perdita di carico, Fig. 5
Perdite di carico in valvole e raccordi
La perdita di carico (HL) in valvole e raccordi è data da:
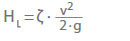
ζ Coefficiente di perdita
Vedi figg. 6 a 12 Perdita di carico
v Velocità di flusso in un’area caratteristica della sezione trasversale A
(per esempio all’ugello) in m/s
g Accelerazione dovuta alla gravità 9,81 m/s2
Fig. 6 Perdita di carico: Diagramma schematico dei disegni delle valvole
Fig. 11 Perdita di carico: Influenza sul coefficiente di perdita ζ dell’arrotondamento del lato interno ed esterno dei gomiti nei condotti quadrati
Fig. 12 Perdita di carico: Coefficienti di perdita ζ per valvole a farfalla, a globo e a saracinesca in funzione del grado di apertura
Le perdite attribuibili al raddrizzamento dei disturbi di flusso su una lunghezza di tubo equivalente a 12 x DN a valle della valvola sono incluse nei coefficienti di perdita secondo la linea guida VDI/VDE 2173. I valori valgono per valvole che hanno un flusso di avvicinamento costante, sono completamente aperte e funzionano con acqua fredda. A seconda delle condizioni del flusso in entrata e in uscita, dei modelli di valvole e degli obiettivi di sviluppo (ad es. valvole economiche o a risparmio energetico), i valori di perdita possono variare notevolmente. Vedi Allegato, Perdita di carico, Fig. 7
Spesso si usa il valore kv invece del coefficiente di perdita (ζ) quando si calcola la perdita di pressione per l’acqua nelle valvole:
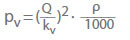
Il valore kv è la portata in m3/h che risulterebbe da una caduta di pressione pv = 1 bar attraverso la valvola per acqua fredda. Descrive la correlazione tra la perdita di pressione (pL) in bar e la portata (Q) in m3/h. Conversione in coefficiente di flusso ζ per acqua fredda:
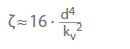
d Diametro di riferimento (nominale) della valvola in cm
Per il calcolo delle perdite di carico nei raccordi, i raccordi di derivazione e gli adattatori richiedono un approccio diverso. Vedere le figure 9 e 10 Perdite di carico
Fig. 9 Perdite di carico: Coefficienti di perdita ζ per i raccordi 
Fig. 10 Perdita di carico: Coefficienti di perdita ζ per adattatori
Per tutti i raccordi si deve distinguere tra due forme di perdita di pressione:
- Perdite di pressione irreversibili (riduzione della pressione)
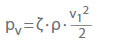
pv Perdita di pressione in Pa
ζ Coefficiente di perdita
ρ Densità in kg/m3
v Velocità di flusso in una sezionesezione in m/s
- Cambiamenti di pressione reversibile del flusso senza attrito secondo l’equazione di Bernoulli
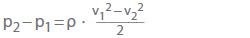
Per flussi accelerati come riduzioni del diametro del tubo, (p2 – p1) è sempre negativo; per i flussi decelerati come le espansioni dei tubi, è sempre positivo. Quando si calcola la variazione di pressione netta come somma aritmetica di pL e (p2 – p1), le perdite di pressione irreversibili devono sempre essere sottratte.
Influenza dei fluidi altamente viscosi sulla curva caratteristica del sistema
Poiché le leggi della fluidodinamica mantengono la loro validità per tutti i fluidi newtoniani, le equazioni e i diagrammi per calcolare i fattori di attrito dei tubi e i coefficienti di perdita delle valvole sono applicabili anche ai fluidi viscosi con una viscosità superiore all’acqua.
Quando si calcola il numero Reynolds Re = v – d / ν , si deve semplicemente sostituire la viscosità cinematica dei fluidi viscosi νz con la viscosità dell’acqua νz.
Questo produce un numero Re più basso e, secondo la Fig. 1 Perdita di carico, un coefficiente di attrito del tubo più grande λz (Nota: l’influenza della rugosità della parete può ora essere spesso ignorata a causa del maggiore spessore dello strato limite nel flusso).
Tutte le perdite di carico nei tubi e nelle valvole calcolate per l’acqua devono essere estrapolate usando il rapporto λz/λw.
La figura 13 delle perdite di carico è adatta anche per un uso pratico generale: il fattore di attrito del tubo λz può essere determinato rapidamente in funzione della portata Q, del diametro interno del tubo d e della viscosità cinematica νz. Bisogna tenere a mente, tuttavia, che il coefficiente λw in questo diagramma è valido solo per tubi idraulicamente lisci (cioè non per tubi ruvidi)! Il corrispondente λw può essere usato per calcolare il rapporto λz/λw.
Come la componente statica della curva caratteristica del sistema Hsys , vedi Fig. 1 Curva caratteristica del sistema e Fig. 2 Testa, non è influenzata dalla viscosità, la componente dinamica della curva caratteristica del sistema per l’acqua può essere ridisegnata come una parabola più ripida per un fluido viscoso.
Influenza dei fluidi non newtoniani sulla curva caratteristica del sistema
Poiché le curve di flusso non sono linee rette di viscosità lineare costante, il calcolo delle perdite di carico è molto complicato. In questo caso, il calcolo delle perdite si basa sull’esperienza con fluidi particolari.