Skewness – Introduzione rapida, esempi e formule
Skewness è un numero che indica in che misura
una variabile è distribuita in modo asimmetrico.
- Esempio di Skewness positiva (destra)
- Esempio di Skewness negativa (sinistra)
- Skewness della popolazione – Formula e calcolo
- Skewness del campione – Formula e calcolo
- Improbabilità in SPSS
- Improbabilità – Implicazioni per l’analisi dei dati
Improbabilità positiva (destra) Esempio
Uno scienziato ha 1,000 persone a completare alcuni test psicologici. Per il test 5, i punteggi del test hanno skewness = 2,0. Un istogramma di questi punteggi è mostrato qui sotto.
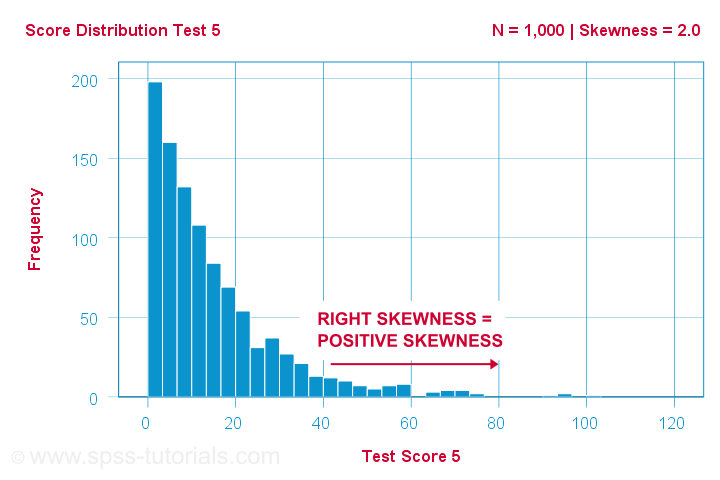
L’istogramma mostra una distribuzione di frequenza molto asimmetrica. La maggior parte delle persone ottiene 20 punti o meno, ma la coda a destra si allunga fino a 90 circa. Questa distribuzione è asimmetrica a destra.
Se ci spostiamo a destra lungo l’asse delle x, andiamo da 0 a 20 a 40 punti e così via. Quindi, verso la destra del grafico, i punteggi diventano più positivi. Pertanto, l’asimmetria destra è un’asimmetria positiva che significa asimmetria > 0. Questo primo esempio ha un’asimmetria = 2,0 come indicato nell’angolo superiore destro del grafico. I punteggi sono fortemente asimmetrici in senso positivo.
Esempio di asimmetria negativa (sinistra)
Un’altra variabile – i punteggi del test 2 risultano avere asimmetria = -1.0. Il loro istogramma è mostrato qui sotto.

La maggior parte dei punteggi sono tra 60 e 100 circa. Tuttavia, la coda sinistra è un po’ allungata. Quindi questa distribuzione è inclinata a sinistra.
Destra: a sinistra, a sinistra. Se seguiamo l’asse delle x verso sinistra, ci spostiamo verso punteggi più negativi. Questo è il motivo per cui l’asimmetria a sinistra è un’asimmetria negativa.E infatti, l’asimmetria = -1,0 per questi punteggi. La loro distribuzione è asimmetrica a sinistra. Tuttavia, è meno asimmetrica – o più simmetrica – del nostro primo esempio che aveva skewness = 2.0.
La distribuzione simmetrica implica zero skewness
Infine, le distribuzioni simmetriche hanno skewness = 0. I punteggi del test 3 – che hanno skewness = 0.1- si avvicinano.

Ora, le distribuzioni osservate sono raramente esattamente simmetriche. Questo si vede soprattutto per alcune distribuzioni teoriche di campionamento. Alcuni esempi sono
- la distribuzione normale (standard);
- la distribuzione t e
- la distribuzione binomiale se p = 0,5.
Queste distribuzioni sono tutte esattamente simmetriche e quindi hanno skewness = 0.000…
Skewness della popolazione – Formula e calcolo
Se volete calcolare le skewness per una o più variabili, lasciate i calcoli a qualche software. Ma – solo per completezza – elencherò comunque le formule.
Se i vostri dati contengono l’intera popolazione, calcolate l’asimmetria della popolazione come:
$$Popolazione;skewness = \Sigma\biggl(\frac{X_i – \mu}{sigma\biggr)^3\cdot\frac{1}{N}$$
dove
- \(X_i\) è ogni singolo punteggio;
- (\mu\) è la media della popolazione;
- (\sigma\) è la deviazione standard della popolazione e
- \(N\) è la dimensione della popolazione.
Per un esempio di calcolo con questa formula, vedere questo foglio di Google (mostrato sotto).
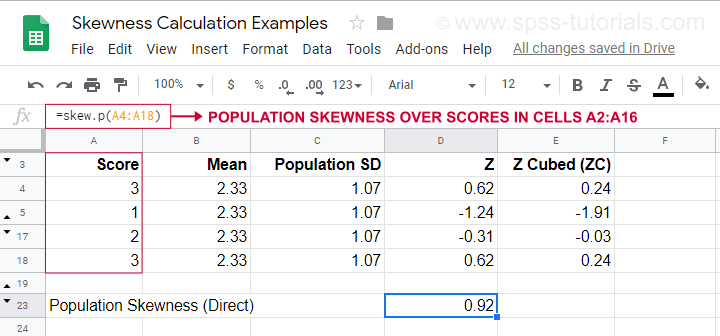
Si può anche ottenere direttamente l’asimmetria della popolazione usando=SKEW.P(…) dove “.P” significa “popolazione”. Questo conferma il risultato del nostro calcolo manuale. Purtroppo, né SPSS né JASP calcolano l’asimmetria della popolazione: entrambi sono limitati all’asimmetria del campione.
Improbabilità campionaria – Formula e calcolo
Se i tuoi dati contengono un semplice campione casuale da una popolazione, usa
$$Sample\;skewness = \frac{N\cdot\Sigma(X_i – \overline{X})^3}{S^3(N – 1)(N – 2)}$$
dove
- \(X_i\) è ogni singolo punteggio;
- (\overline{X}}) è la media del campione;
- \(S) è la deviazione standard del campione e
- \(N) è la dimensione del campione.
Un esempio di calcolo è mostrato in questo Googlesheet (mostrato sotto).
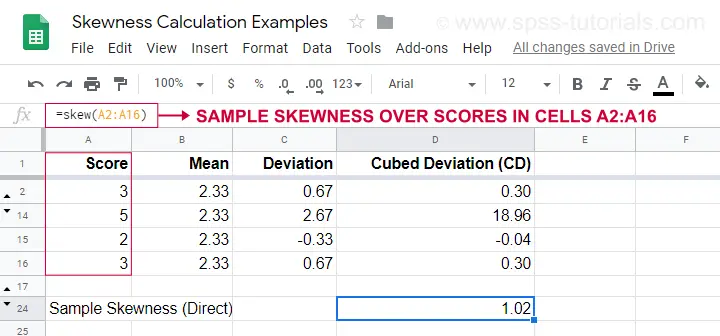
Un’opzione più semplice per ottenere l’asimmetria del campione è usare=SKEW(…).che conferma il risultato del nostro calcolo manuale.
Improbabilità in SPSS
Prima di tutto, “l’improbabilità” in SPSS si riferisce sempre all’improbabilità del campione: assume tranquillamente che i vostri dati contengano un campione piuttosto che un’intera popolazione. Ci sono molte opzioni per ottenerla. Il mio preferito è tramite MEANS perché la sintassi e l’output sono puliti e semplici. Le schermate qui sotto vi guidano.

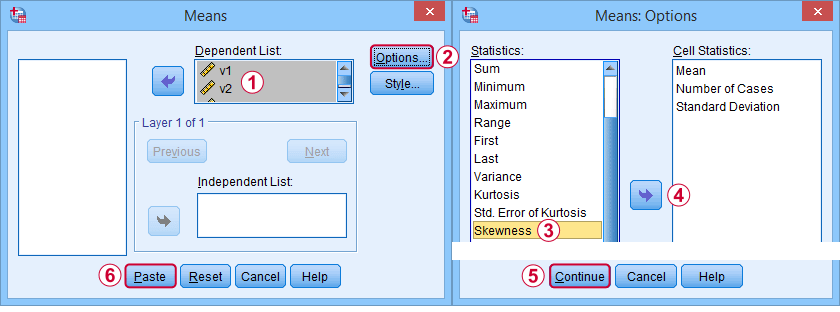
La sintassi può essere semplice comemeans v1 to v5
/cells skew.Una tabella molto completa -inclusa media, deviazioni standard, mediane e altro- viene eseguita dameans v1 to v5
/cells count min max mean median stddev skew kurt.Il risultato è mostrato qui sotto.
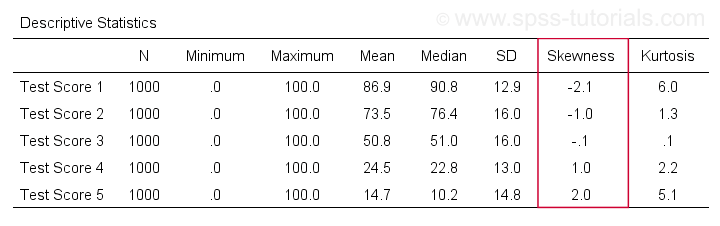
Skewness – Implicazioni per l’analisi dei dati
Molte analisi -ANOVA, t-test, regressione e altre- richiedono l’assunzione di normalità: le variabili dovrebbero essere distribuite normalmente nella popolazione. La distribuzione normale ha skewness = 0. Quindi osservare una sostanziale skewness in alcuni dati del campione suggerisce che l’assunzione di normalità è violata.
Tali violazioni della normalità non sono un problema per campioni di grandi dimensioni – ad esempio N > 20 o 25 o giù di lì. In questo caso, la maggior parte dei test sono robusti contro tali violazioni. Questo è dovuto al teorema del limite centrale. In breve, per campioni di grandi dimensioni, l’asimmetria non è
un vero problema per i test statistici; tuttavia, l’asimmetria è spesso associata a grandi deviazioni standard. Queste possono risultare in grandi errori standard e basso potere statistico. Così, una sostanziale asimmetria può diminuire la possibilità di rifiutare qualche ipotesi nulla per dimostrare qualche effetto. In questo caso, un test non parametrico può essere una scelta più saggia in quanto può avere più potenza. Le violazioni della normalità rappresentano una minaccia reale
per piccole dimensioni del campione, ad esempio N < 20 o giù di lì. Con piccole dimensioni del campione, molti test non sono robusti contro una violazione dell’ipotesi di normalità. La soluzione -ancora una volta- è usare un test non parametrico perché questi non richiedono la normalità.
Infine, ma non meno importante, non c’è nessun test statistico per esaminare se l’asimmetria della popolazione = 0. Un modo indiretto per verificare questo è un test di normalità come
- il test di normalità Kolmogorov-Smirnov e
- il test di normalità Shapiro-Wilk.
Tuttavia, quando la normalità è veramente necessaria -con piccole dimensioni del campione- tali test hanno una bassa potenza: possono non raggiungere la significatività statistica anche quando le deviazioni dalla normalità sono gravi. Così, forniscono principalmente un falso senso di sicurezza.




