Oppervlakte van een cilinder – Uitleg en voorbeelden
Voordat we ons buigen over de oppervlakte van een cilinder, geven we eerst een overzicht van een cilinder. In de meetkunde is een cilinder een driedimensionale figuur met twee evenwijdig aan elkaar liggende cirkelvormige grondvlakken en een gekromd oppervlak.
Hoe bepaal je de oppervlakte van een cilinder?
De oppervlakte van een cilinder is de som van twee evenwijdige en congruente cirkelvormige vlakken en het gekromde oppervlak.
In dit artikel wordt besproken hoe u de totale oppervlakte en de zijdelingse oppervlakte van een cilinder kunt vinden.
Om de oppervlakte van een cilinder te berekenen, moet u de basisoppervlakte (B) en de gekromde oppervlakte (CSA) vinden. De oppervlakte of de totale oppervlakte van een cilinder is dus gelijk aan de som van de basisoppervlakte maal twee en de oppervlakte van het gekromde oppervlak.
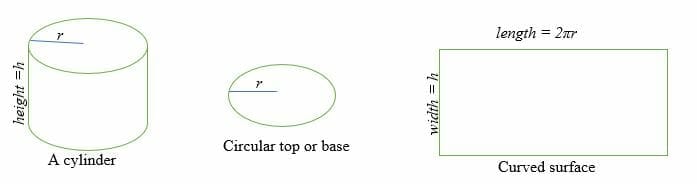
Het gekromde oppervlak van een cilinder is gelijk aan een rechthoek waarvan de lengte 2πr is en de breedte h.
Waarbij r = straal van het cirkelvormige vlak en h = hoogte van de cilinder.
De oppervlakte van het gebogen oppervlak = Oppervlakte van een rechthoek =l x b = πdh
De oppervlakte van het grondvlak, B = Oppervlakte van een cirkel = πr2
De formule voor de oppervlakte van een cilinder
De formule voor de totale oppervlakte van een cilinder is gegeven als:
Totale oppervlakte van een cilinder = 2πr2 + 2πrh
TSA = 2πr2 + 2πrh
Waarbij 2πr2 de oppervlakte van het bovenste en onderste cirkelvormige vlak is, en 2πrh de oppervlakte van het gekromde oppervlak.
Door 2πr als een gemeenschappelijke factor van de RHS te nemen, krijgen we;
TSA = 2πr (h + r) ……………………………………. (Oppervlakte van een cilinder formule)
Laten we voorbeeldopgaven oplossen met betrekking tot de oppervlakte van een cilinder.
Voorbeeld 1
Vind de totale oppervlakte van een cilinder met een straal van 5 cm en een hoogte van 7 cm.
Oplossing
Op grond van de formule,
TSA = 2πr (h + r)
= 2 x 3.14 x 5(7 + 5)
= 31,4 x 12
= 376,8 cm2
Voorbeeld 2
Vind de straal van een cilinder waarvan de totale oppervlakte 2136,56 vierkante voet is, en de hoogte 3 voet.
Oplossing
Gegeven:
TSA = 2136.56 vierkante voet
Hoogte, h = 3 voet
Maar, TSA = 2πr (h + r)
2136,56 =2 x 3,14 x r (3 + r)
2136,56 = 6.28r (3 + r)
Door de distributieve eigenschap van vermenigvuldiging op de RHS, hebben we,
2136.56 = 18.84r + 6.28r2
Deel elke term door 6.28
340.22 = 3r + r2
r2 + 3r – 340,22 = 0 ……… (een kwadratische vergelijking)
Door de vergelijking op te lossen met de kwadratische formule, krijgen we,
r = 17
Daaruit is de straal van de cilinder 17 voet.
Voorbeeld 3
De kosten van het verven van een cilindrische bak bedragen $ 0,04 per cm2. Bereken de kosten van het verven van 20 bakken met een straal van 50 cm en een hoogte van 80 cm.
Oplossing
Bereken de totale oppervlakte van 20 bakken.
TSA = 2πr (h + r)
= 2 x 3.14 x 50 (80 + 50)
= 314 x 130
= 40820 cm2
De totale oppervlakte van 20 containers = 40.820 cm2 x 20
=816.400 cm2
De kosten van het schilderen = 816.400 cm2 x $0.04 per cm2
= $32.656.
Hieruit volgt dat de kosten voor het verven van 20 containers $32.656.
Voorbeeld 4
Bepaal de hoogte van een cilinder als de totale oppervlakte 2552 in2 bedraagt en de straal 14 in is.
Oplossing
Gegeven:
TSA = 2552 in2
Radius, r = 14 in.
Maar, TSA = 2πr (h + r)
2552 = 2 x 3.14 x 14 (14 + h)
2552 = 87,92(14 + h)
Deel beide zijden door 87,92 om te krijgen,
29.026 = 14 + h
Trek aan beide zijden 14 af.
h = 15
Daaruit volgt dat de hoogte van de cilinder 15 in is.
Lateraal oppervlak van een cilinder
Zoals eerder gezegd, is de oppervlakte van het gebogen oppervlak van een cilinder wat men noemt het laterale oppervlak. Eenvoudig gezegd is de laterale oppervlakte van een cilinder de oppervlakte van een cilinder, exclusief de oppervlakte van het grondvlak en de bodem (cirkelvormig oppervlak).
De formule geeft de laterale oppervlakte van een cilinder;
LSA = 2πrh
Voorbeeld 5
Vind de laterale oppervlakte van een cilinder met een diameter van 56 cm en een hoogte van 20 cm.
Oplossing
Gegeven:
Diameter = 56 cm, dus straal, r =56/2 = 28 cm
Hoogte, h = 20 cm
Met behulp van de formule,
LSA = 2πrh
= 2 x 3.14 x 28 x 20
= 3516,8 cm2.
Dus de zijdelingse oppervlakte van de cilinder is 3516,8 cm2.
Voorbeeld 6
De zijdelingse oppervlakte van een cilinder is 144 ft2. Als de straal van de cilinder 7 ft is, bepaal dan de hoogte van de cilinder.
Oplossing
Gegeven;
LSA = 144 ft2
Radius, r = 7 ft




