Beginning Algebra

Beginning Algebra

Płaszczyzna współrzędnych została opracowana wieki temu (dokładnie w 1637 roku) i udoskonalona przez francuskiego matematyka René Descartesa. Na jego cześć system ten jest czasami nazywany kartezjańskim układem współrzędnych. Płaszczyzna współrzędnych może być używana do wykreślania punktów i linii. Ten system pozwala nam opisywać zależności algebraiczne w sensie wizualnym, a także pomaga nam tworzyć i interpretować pojęcia algebraiczne.

Komponenty płaszczyzny współrzędnych

Prawdopodobnie używałeś już wcześniej płaszczyzny współrzędnych. Na przykład, czy kiedykolwiek używałeś siatkowej nakładki do odwzorowania pozycji obiektu? (Często robi się to również z mapami drogowymi.)

Ta „mapa” używa poziomej i pionowej siatki do przekazania informacji o położeniu obiektu. Zauważ, że litery A-F są wymienione na górze, a liczby 1-6 są wymienione wzdłuż lewej krawędzi. Ogólna lokalizacja dowolnego elementu na tej mapie może być znaleziona poprzez użycie litery i numeru kwadratu siatki. Na przykład, można znaleźć element, który istnieje w kwadracie „4F”, przesuwając palec wzdłuż poziomu do litery F, a następnie prosto w dół, tak aby znaleźć się w linii z 4. Znajdziesz niebieski dysk jest w tym miejscu na mapie.

Płaszczyzna współrzędnych ma podobne elementy do siatki pokazanej powyżej. Składa się z osi poziomej i osi pionowej, linii liczbowych, które przecinają się pod kątem prostym. (Są one do siebie prostopadłe.)

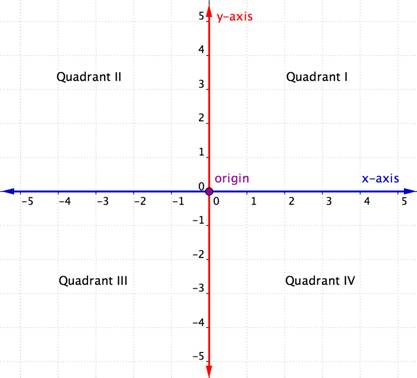
Oś pozioma na płaszczyźnie współrzędnych nazywa się osią x. Oś pionowa jest nazywana osią y. Punkt, w którym przecinają się te dwie osie nazywamy początkiem. Początek znajduje się w punkcie 0 na osi x i 0 na osi y.

Lokalizacje na płaszczyźnie współrzędnych są opisywane jako uporządkowane pary. Para uporządkowana mówi o położeniu punktu przez odniesienie położenia punktu wzdłuż osi x (pierwsza wartość pary uporządkowanej) i wzdłuż osi y (druga wartość pary uporządkowanej).

W parze uporządkowanej, takiej jak (x, y), pierwsza wartość jest nazywana współrzędną x, a druga wartość jest współrzędną y. Zauważ, że współrzędna x jest wymieniona przed współrzędną y. Ponieważ początek ma współrzędną x równą 0 i współrzędną y równą 0, jego para uporządkowana jest zapisana (0, 0).

Rozważ punkt poniżej.

Aby zidentyfikować położenie tego punktu, zacznij od początku (0, 0) i przesuwaj się w prawo wzdłuż osi x, aż znajdziesz się pod punktem. Spójrz na etykietę na osi x. Cyfra 4 oznacza, że od początku przesunęliśmy się o cztery jednostki w prawo wzdłuż osi x. Jest to współrzędna x, pierwsza liczba w parze uporządkowanej.

Od 4 na osi x przesuń się do punktu i zauważ liczbę, z którą pokrywa się on na osi y. Liczba 3 oznacza, że po opuszczeniu osi x przebyłeś drogę o 3 jednostki w górę w kierunku pionowym, czyli w kierunku osi y. Ta liczba to współrzędna y. Ta liczba jest współrzędną y, drugą liczbą w uporządkowanej parze. Mając współrzędną x równą 4 i współrzędną y równą 3, mamy parę uporządkowaną (4, 3).

Przyjrzyjrzyjmy się innemu przykładowi.

Opisz punkt przedstawiony jako uporządkowana para

Wykreślanie punktów na płaszczyźnie współrzędnych

Teraz, gdy wiesz jak używać osi x i y, możesz również wykreślić uporządkowaną parę. Pamiętaj tylko, że oba procesy zaczynają się w punkcie początkowym – na początku! Poniższy przykład pokazuje, jak wykreślić parę uporządkowaną (1,3).

W poprzednim przykładzie zarówno współrzędna x jak i y były dodatnie. Gdy jedna (lub obie) ze współrzędnych uporządkowanej pary jest ujemna, będziesz musiał poruszać się w kierunku ujemnym wzdłuż jednej lub obu osi. Rozważ poniższy przykład, w którym obie współrzędne są ujemne.

Kroki wykreślania punktu są podsumowane poniżej.

Wykreślanie punktów na płaszczyźnie współrzędnych

Zidentyfikuj kwadranty i wykorzystaj je do wykreślania punktów

Przecinające się osie x i y płaszczyzny współrzędnych dzielą ją na cztery części. Te cztery sekcje nazywamy kwadrantami. Kwadranty są nazwane przy użyciu liczb rzymskich I, II, III i IV, zaczynając od prawego górnego kwadrantu i poruszając się przeciwnie do ruchu wskazówek zegara.

Pary uporządkowane w obrębie dowolnego konkretnego kwadrantu mają pewne wspólne cechy. Przyjrzyj się każdemu kwadrantowi na poniższym wykresie. Co zauważyłeś na temat znaków współrzędnych x i y punktów w każdym kwadrancie?

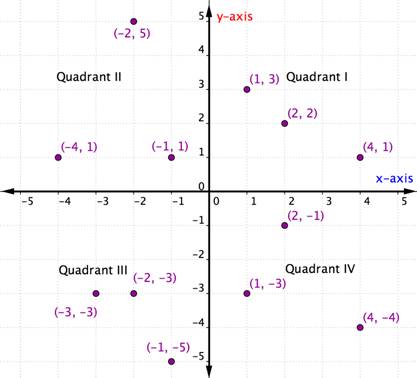
W obrębie każdego kwadrantu znaki współrzędnych x i y każdej pary uporządkowanej są takie same. Są one również zgodne z pewnym wzorem, który przedstawiono w poniższej tabeli.

Kwadrant	Ogólna postać punktu w tym kwadrancie	Przykład	Opis
I	(+,+)	(5,4)	Rozpoczynając od początku, idź wzdłuż osi x w kierunku dodatnim (w prawo) i wzdłuż osi y w kierunku dodatnim (w górę).
II	(-,+)	(-5,4)	Startując od początku, idź wzdłuż osi x w kierunku ujemnym (w lewo) i wzdłuż osi y w kierunku dodatnim (w górę).
III	(-,-)	(-5,-4)	Startując od początku, idź wzdłuż osi x w kierunku ujemnym (w lewo) i wzdłuż osi y w kierunku ujemnym (w dół).
IV	(+,-)	(5,-4)	Rozpoczynając od początku, idź wzdłuż osi x w kierunku dodatnim (w prawo) i wzdłuż osi y w kierunku ujemnym (w dół).

Odkąd wiesz o kwadrantach na płaszczyźnie współrzędnych, możesz określić kwadrant uporządkowanej pary nawet bez wykresu, patrząc na powyższy wykres. Oto inny sposób, by o tym pomyśleć.

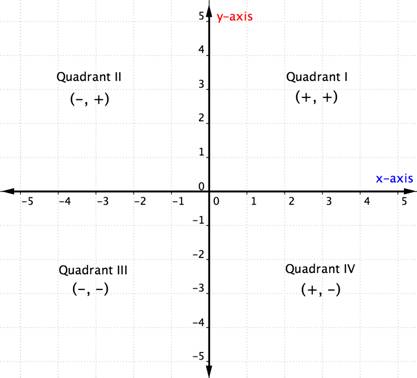
Poniższy przykład pokazuje, jak określić położenie punktu w ćwiartce poprzez zastanowienie się nad znakami jego współrzędnych. Zastanowienie się nad położeniem ćwiartki przed wykreśleniem punktu może pomóc w uniknięciu błędu. Jest to również przydatna wiedza do sprawdzenia, czy punkt został poprawnie wykreślony.

Co się stanie, jeśli para uporządkowana ma współrzędną x lub y równą zero? Poniższy przykład przedstawia wykres pary uporządkowanej (0,4).

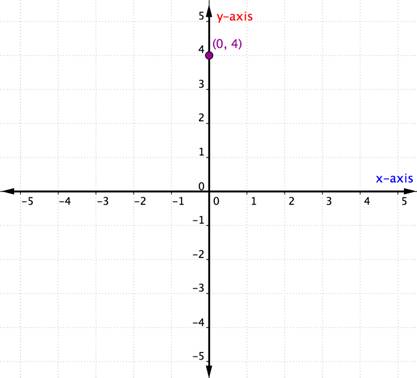
Punkt położony na jednej z osi nie jest uważany za znajdujący się w kwadrancie. Znajduje się on po prostu na jednej z osi. Gdy współrzędna x jest równa 0, punkt znajduje się na osi y. Podobnie każdy punkt, którego współrzędna x jest równa 0, znajduje się na osi y. Podobnie każdy punkt, który ma współrzędną y równą 0, będzie znajdował się na osi x.

Identyfikuj kwadranty i używaj ich do wykreślania punktów

Podsumowanie

Płaszczyzna współrzędnych jest systemem do wykreślania i opisywania punktów i linii. Płaszczyzna współrzędnych składa się z osi poziomej (x-) i pionowej (y-). Punkt przecięcia tych linii tworzy początek, którym jest punkt (0,0). Płaszczyzna współrzędnych jest podzielona na cztery kwadranty. Razem, te cechy układu współrzędnych pozwalają na graficzne przedstawienie i komunikację na temat punktów, linii i innych pojęć algebraicznych.