Centrifugal Pump Lexicon
Straty wysokości są wynikiem tarcia o ścianki we wszystkich typach rurociągów oraz lokalnych oporów przepływu, na przykład w zaworach i armaturze (patrz również Strata ciśnienia).
Zalecane prędkości przepływu
- Dla zimnej wody:
Przewód ssący 0.7-1,5 m/s
Przewód odprowadzający 1,0-2,0 m/s - Dla wody ciepłej:
Przewód odprowadzający 0,5-1,0 m/s
Przewód odprowadzający 1,5-3,5 m/s
Równanie na stratę wysokości głowy przepływu w prostej długości rurociągu o przekroju kołowym wynosi:
λ Współczynnik tarcia rur
L Długość rury w m
d Średnica wewnętrzna rury w m
v Prędkość przepływu w przekroju poprzecznym w m/s
(= 4 Q / π d2 przy czym Q w m3/s)
g Przyspieszenie wywołane grawitacją w m/s2
patrz rys. 1 i 4 Strata wysokości
Współczynnik tarcia rur został wyznaczony doświadczalnie. Zależy on jedynie od stanu przepływu obsługiwanej cieczy oraz od względnej chropowatości (d/k) rur, przez które przepływa ciecz. Dla nieokrągłych przekrojów rur stosuje się średnicę zastępczą w ujęciu płynno-mechanicznym (d):
A Przekrój poprzeczny w m2
U Zwilżony obwód przekroju poprzecznego w m
(nie uwzględnia się powierzchni swobodnej kanału otwartego)
Stan przepływu określa liczba Reynoldsa (Re) zgodnie z prawami powinowactwa. Dla rur o przekroju kołowym obowiązuje:
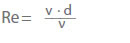
v Prędkość przepływu w przekroju poprzecznym w m/s
(= 4 Q / π d2 przy Q w m3/s)
ν Lepkość kinematyczna w m2/s
(dla wody w temperaturze 20 °C: 1.00 – 10 – 6 m2/s)
d Średnica wewnętrzna rury w m
Patrz rys. 4 Strata wysokości
Dla hydraulicznie gładkich rur, takich jak gładkie ciągnione rury metalowe lub z tworzyw sztucznych (np. PE lub PVC), lub w przypadku przepływu laminarnego, można obliczyć współczynnik tarcia rury (λ). Dla przepływu laminarnego w rurze o liczbie Reynoldsa mniejszej niż 2320 współczynnik tarcia rury jest niezależny od chropowatości:
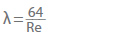
Jeśli przepływ jest turbulentny lub liczba Reynoldsa jest większa niż 2320, współczynnik tarcia rury w hydraulicznie gładkich rurach można przedstawić za pomocą empirycznego równania według Ecka (ze względu na fakt, że odchylenia są mniejsze niż 1%, jeśli liczba Reynoldsa jest mniejsza niż 108).
Współczynnik tarcia rury (λ) zależy również od kolejnego bezwymiarowego parametru, tj. od względnej chropowatości wewnętrznej powierzchni rury (d/k). Oba muszą być podane w tej samej jednostce (np. mm).
Patrz rys. 1 Strata wysokości
(k) jest średnią bezwzględną chropowatością wewnętrznej powierzchni rury, dla której dostępne są przybliżone wartości w zależności od materiału i procesów produkcyjnych. Patrz rys. 2 Strata wysokości
Rys. 2 Strata wysokości: Estimates of mean peak-to-valley heights k (absolute roughness) of pipes
Powyżej krzywej granicznej, współczynnik tarcia rury (λ) zależy wyłącznie od względnej chropowatości rury (d/k). Patrz Rys. 1 Strata wysokości
Dla tego regionu można zastosować następujące równanie empiryczne Moody’ego:
Do celów praktycznych, strata wysokości (HL) na 100 m prostej rury stalowej jest pokazana na wykresie jako funkcja natężenia przepływu (Q) i średnicy wewnętrznej rury (d).
Patrz Rys. 3 Strata głowicy
Wartości te są ważne tylko dla zimnej, czystej wody lub dla cieczy o tej samej lepkości kinematycznej, dla całkowicie wypełnionych rur i dla bezwzględnej chropowatości wewnętrznej powierzchni rury k = 0.05 mm.
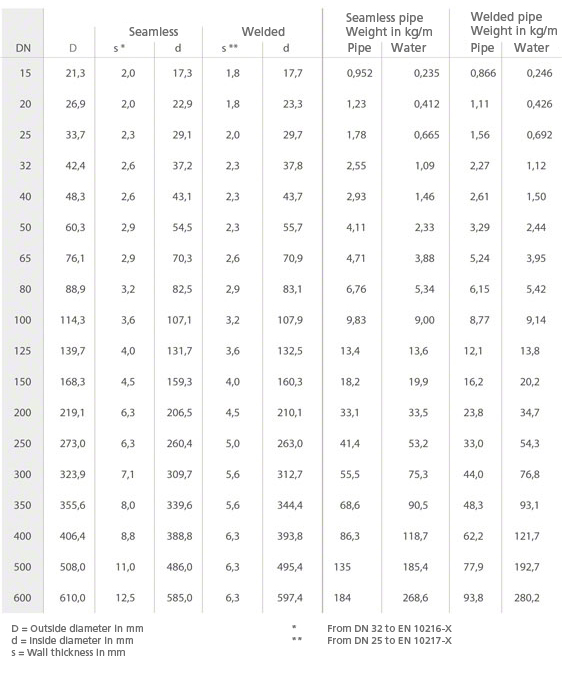
Wymiary, ciężary, napełnienie wodą dla nowych rur stalowych bez szwu lub spawanych wzdłużnie
Patrz załącznik, Strata głowy, Rys. 4
Wpływ zwiększonej chropowatości powierzchni k zostanie przedstawiony poniżej dla często stosowanego zestawu zakresów parametrów (średnica nominalna DN = 50 do 300, prędkość przepływu v = 0,8 do 3,0 m/s). Patrz Rys. 3 Strata głowy
Jasnoniebieski region odpowiada podobnie oznaczonemu regionowi dla średniej bezwzględnej chropowatości k = 0,05 mm.
Patrz Rys. 1 Strata głowy
Dla chropowatości zwiększonej o współczynnik 6 (lekko inkrustowana stara rura stalowa o k = 0,30 = 300 μm (0.30 mm), współczynniki tarcia rur (i związane z nimi proporcjonalne straty wysokości) w obszarze ciemnoniebieskim są tylko o 25 – 60 % wyższe niż poprzednio.
Patrz Rys. 1 Strata wysokości
W przypadku rur kanalizacyjnych należy wziąć pod uwagę zwiększoną chropowatość spowodowaną zabrudzeniem. W przypadku rur narażonych na ekstremalne inkrustacje rzeczywista strata wysokości może być określona tylko doświadczalnie. Odchylenia od średnicy nominalnej znacznie zmieniają straty wysokości, ponieważ średnica wewnętrzna rury występuje w równaniu do piątej potęgi potęgi.
Na przykład zmniejszenie średnicy wewnętrznej o 5 % prowadzi do zwiększenia strat wysokości aż o 30 %. Dlatego ważne jest, aby w obliczeniach nie zastępować średnicy wewnętrznej tylko średnicę nominalną.
Straty ciśnienia w rurach z tworzyw sztucznych lub gładkich ciągnionych rurach metalowych są bardzo małe dzięki gładkim powierzchniom rur. Ustalone straty ciśnienia obowiązują dla wody w temperaturze 10 °C. W innych temperaturach straty dla rur z tworzyw sztucznych muszą być pomnożone przez określony współczynnik korekcyjny temperatury, aby uwzględnić ich większą rozszerzalność cieplną. W przypadku ścieków lub innej nieuzdatnionej wody należy uwzględnić dodatkowe 20-30 % straty wysokości dla potencjalnych osadów.
Straty wysokości dla rur z tworzyw sztucznych i gładkich ciągnionych rur metalowych
Patrz załącznik, Straty wysokości, rys. 5
Straty głowicy w zaworach i armaturze
Straty głowicy (HL) w zaworach i armaturze są dane przez:
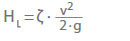
ζ Współczynnik strat
Patrz rys. 6 do 12 Strata głowicy
v Prędkość przepływu w charakterystycznym przekroju poprzecznym A
(np. na dyszy) w m/s
g Przyspieszenie ziemskie 9,81 m/s2
Rys. 6 Strata głowicy: Schemat konstrukcji zaworów
Rys. 11 Strata głowicy: Wpływ na współczynnik strat ζ zaokrąglenia wewnętrznej i zewnętrznej strony kolan w kanałach kwadratowych
Rys. 12 Strata głowicy: Współczynniki strat ζ dla zaworów motylkowych, grzybkowych i zasuw w zależności od stopnia otwarcia
Straty przypisywane prostowaniu zakłóceń przepływu na długości przewodu równej 12 x DN za zaworem są uwzględnione we współczynnikach strat zgodnie z wytyczną VDI/VDE 2173. Wartości te dotyczą zaworów o stałym przepływie wejściowym, całkowicie otwartych i zasilanych zimną wodą. W zależności od warunków przepływu na wlocie i wylocie, modeli zaworów i celów projektowych (np. tanie lub energooszczędne zawory), wartości strat mogą się znacznie różnić. Patrz Załącznik, Strata głowicy, Rys. 7
Często wartość kv jest używana zamiast współczynnika strat (ζ) przy obliczaniu strat ciśnienia dla wody w zaworach:
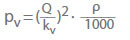
Wartość kv to natężenie przepływu w m3/h, które wynikałoby ze spadku ciśnienia pv = 1 bar przez zawór dla zimnej wody. Opisuje ona zależność pomiędzy stratą ciśnienia (pL) w barach a natężeniem przepływu (Q) w m3/h. Przeliczenie na współczynnik przepływu ζ dla wody zimnej:
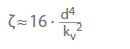
d Średnica referencyjna (nominalna) zaworu w cm
Obliczanie strat wysokości podnoszenia w armaturze, rozgałęzieniach i adapterach wymaga innego podejścia. Patrz rys. 9 i 10 Strata głowicy
Rys. 9 Strata głowicy: Współczynniki strat ζ dla armatury 
Rys. 10 Straty głowicy: Współczynniki strat ζ dla złączek
Dla wszystkich złączek należy rozróżnić dwie formy strat ciśnienia:
- Odwracalne straty ciśnienia (obniżenie ciśnienia)
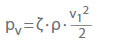
pv Strata ciśnienia w Pa
ζ Współczynnik strat
ρ Gęstość w kg/m3
v Prędkość przepływu w przekrojuPrzekrój w m/s
- Odwracalne zmiany ciśnienia przepływu bez tarcia zgodnie z równaniem Bernoulliego
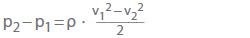
Dla przepływów przyspieszonych, takich jak zmniejszenie średnicy rury, (p2 – p1) jest zawsze ujemne; dla przepływów spowolnionych, takich jak rozszerzanie się rur, jest zawsze dodatnie. Przy obliczaniu zmiany ciśnienia netto jako sumy arytmetycznej pL i (p2 – p1) należy zawsze odjąć nieodwracalne straty ciśnienia.
Wpływ płynów o dużej lepkości na krzywą charakterystyczną układu
Ponieważ prawa dynamiki płynów zachowują swoją ważność dla wszystkich płynów newtonowskich, równania i wykresy do obliczania współczynników tarcia rur i współczynników strat dla zaworów mają również zastosowanie do płynów lepkich o lepkości większej niż woda.
Przy obliczaniu liczby Reynoldsa Re = v – d / ν , należy po prostu zastąpić lepkość kinematyczną płynów lepkich νz lepkością wody νz.
W ten sposób uzyskuje się niższą liczbę Re i, zgodnie z rys. 1 Strata głowy, większy współczynnik tarcia rurowego λz (Uwaga: wpływ chropowatości ścianki można teraz często pominąć ze względu na większą grubość warstwy granicznej w przepływie).
Wszystkie straty ciśnienia w rurach i zaworach obliczone dla wody należy ekstrapolować stosując stosunek λz/λw.
Rysunek 13 Strata głowy jest również odpowiedni do ogólnego praktycznego zastosowania: współczynnik tarcia rurowego λz można szybko wyznaczyć jako funkcję natężenia przepływu Q, średnicy wewnętrznej rury d i lepkości kinematycznej νz. Należy jednak pamiętać, że współczynnik λw podany na tym wykresie obowiązuje tylko dla rur gładkich hydraulicznie (tzn. nie dla rur chropowatych)! Odpowiedni współczynnik λw można wykorzystać do obliczenia stosunku λz/λw.
Jako że na składową statyczną charakterystyki systemu Hsys , patrz Rys. 1 Charakterystyka systemu i Rys. 2 Głowica, nie ma wpływu lepkość, składowa dynamiczna charakterystyki systemu dla wody może być przerysowana jako bardziej stroma parabola dla płynu lepkiego.
Wpływ płynów nienewtonowskich na krzywą charakterystyki układu
Ponieważ krzywe przepływu nie są liniami prostymi o stałej lepkości liniowej, obliczanie strat głowicy jest bardzo kłopotliwe. W tym przypadku obliczenia strat opierają się na doświadczeniu z konkretnymi cieczami.