Definicja funkcji falowej
Cząstki fundamentalne, takie jak elektrony, mogą być opisane jako cząstki lub fale.
Elektrony mogą być opisane za pomocą funkcji falowej.Symbolem funkcji falowej jest grecka litera psi, Ψ lub ψ.

Funkcja falowa Ψ jest wyrażeniem matematycznym.Niesie ona istotną informację o elektronie, z którym jest związana:z funkcji falowej otrzymujemy energię elektronu, jego moment pędu i orientację orbitalną w postaci liczb kwantowych n, l, i ml.
Funkcja falowa może mieć znak dodatni lub ujemny.Znak ten jest ważny w obliczeniach.Jest on również ważny, gdy funkcje falowe dwóch lub więcej atomów łączą się, tworząc cząsteczkę.
Funkcje falowe o podobnych znakach (fale w fazie) będą interferować konstruktywnie, prowadząc do możliwości tworzenia wiązań.Funkcje falowe o niepodobnych znakach (fale poza fazą) będą interferować destruktywnie.
W 1926 roku Erwin Schrödinger wydedukował funkcję falową dla najprostszego ze wszystkich atomów, wodoru.Rozwiązanie równania Schrödingera umożliwia naukowcom wyznaczenie funkcji falowych dla elektronów w atomach i cząsteczkach.
Równanie Schrödingera jest równaniem mechaniki kwantowej: obliczone funkcje falowe mają dyskretne, dozwolone wartości dla elektronów związanych w atomach i cząsteczkach;wszystkie inne wartości są zabronione.
Oprócz znaczenia Ψ, jego kwadrat Ψ2 ma również ogromne znaczenie w chemii.
Ψ2 jest gęstością prawdopodobieństwa.Mówi nam, gdzie najprawdopodobniej znajdzie się elektron w przestrzeni wokół jądra.
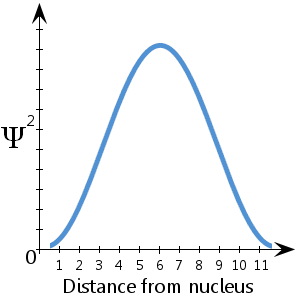
Na przykład, na (fikcyjnym) schematycznym wykresie pokazującym zależność Ψ2 od odległości od jądra, widzimy, że elektron jest najbardziej prawdopodobny do znalezienia pomiędzy około 5-7 jednostkami od jądra.Widzimy również, że istnieje znikome prawdopodobieństwo, że elektron będzie w jądrze lub w odległości większej niż około 11½ jednostki od jądra.
Istnieje stuprocentowe prawdopodobieństwo, że elektron gdzieś jest – innymi słowy prawdopodobieństwo równe 1.
Ψ można dokładnie obliczyć tylko dla atomów z jednym elektronem, czyli H, He+, Li2+, Be3+, B4+, C5+, itd.W języku matematycznym mówimy, że analityczne rozwiązania dla Ψ są możliwe tylko dla układów jednoelektronowych.Układy jednoelektronowe są często określane jako wodorkowe – co oznacza „jak wodór.”
Dla wszystkich innych atomów, jonów i cząsteczek nie są możliwe analityczne rozwiązania dla Ψ; do jego obliczenia konieczne są metody przybliżone.
Ψ2 i orbitale wodorowe
Wykreślenie gęstości prawdopodobieństwa wodoru (tj.Ψ2) dla różnych liczb kwantowych pozwala nam zobrazować przestrzeń, skupioną na jądrze, którą zajmują elektrony. Różne rozkłady Ψ2 to orbitale elektronowe wodoru.Orbital, który jest faktycznie zajęty jest określany przez ilość energii, jaką posiada elektron.
Przykłady orbitali wodoru
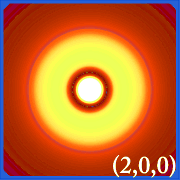
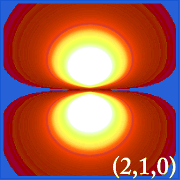

.





.




