Entropia – filar termodynamiki i teorii informacji
Entropia to niejasny, ale potężny termin, który stanowi podstawę wielu kluczowych idei w termodynamice i teorii informacji. Został on po raz pierwszy zidentyfikowany przez naukowców fizycznych w XIX wieku i działał jako zasada przewodnia dla wielu rewolucyjnych technologii rewolucji przemysłowej. Jednak termin ten pomógł również zapoczątkować erę informacji, gdy pojawił się w przełomowej pracy matematyka Claude’a Shannona A Mathematical Theory of Communication. Jak więc jeden termin może być odpowiedzialny za dwa przełomowe odkrycia, w odstępie około stu lat, w pokrewnych, choć odmiennych dziedzinach?
Po pierwsze, zacznijmy od tego, jak entropia jest interpretowana w naukach fizycznych. Pierwsze Prawo Termodynamiki stanowi, że w każdym zamkniętym systemie energia nie może być ani stworzona, ani zniszczona. Drugie Prawo, znane również jako Prawo Entropii, mówi, że w układzie otwartym energia zawsze przepływa z wyższego stężenia do niższego, aby osiągnąć równowagę termodynamiczną. Co to oznacza w praktyce? Oznacza to, że Twój kubek kawy w końcu wystygnie, a lód w napoju z czasem się roztopi, lub że narzędzie włożone do ognia rozgrzeje się, ponieważ energia z płomienia przenosi się na cząsteczki żelaza, ale ostygnie po jego usunięciu, ponieważ energia rozprowadza się w nowym otoczeniu.

Samo pojęcie entropii odnosi się do stanu nieuporządkowania w danym systemie. Energia w skoncentrowanej i użytecznej formie jest uważana za uporządkowaną, podczas gdy energia w formie rozproszonej i niedostępnej jest uważana za nieuporządkowaną.
Entropia porusza się tylko w jednym kierunku – w kierunku równowagi – chyba że działa na nią siła spoza systemu, a nawet wtedy siły zewnętrzne, takie jak systemy biologiczne, tylko tymczasowo udaje się odwrócić proces entropii i ostatecznie ustąpić (poprzez śmierć). Każda roślina czy zwierzę jest złożonym systemem energetycznym, który przeżywa, równoważąc proces entropii i gromadząc dostępną, uporządkowaną energię ze środowiska, a następnie wydzielając odpady pozbawione składników odżywczych. Ale przepływ energii w systemie żywym w końcu degraduje jego strukturę fizyczną, powodując rozpad i śmierć organizmu (miejmy nadzieję, że ukończywszy swój ostateczny cel, jakim jest reprodukcja). Ciało energii, już nie żyjące, rozpadnie się i rozproszy w otaczającym środowisku – i w równowadze termodynamicznej.
Teoretycznie entropia zatrzyma swój stały marsz dopiero wtedy, gdy doprowadzi do śmierci cieplnej wszechświata – ostatecznego stanu końcowego, w którym nie ma wolnej energii. Wszystko na ziemi i w kosmosie w końcu rozszerzy się, eksploduje, umrze i rozprowadzi wolną energię równomiernie w tym, co jest naprawdę największym zamkniętym systemem ze wszystkich: we wszechświecie. W ten sposób entropia jest uniwersalnym prawem podobnym do grawitacji, ponieważ działa zarówno w najmniejszych, jak i największych skalach biofizyki.
Gospodarki to organizmy, a nie pralki
Entropia odnosi się również do gospodarki. Proces entropii w organizmie, polegający na pozyskiwaniu dostępnej energii z otoczenia i przekształcaniu jej w energię nieuporządkowaną, dotyczy również grup organizmów. Społeczeństwa pobierają źródła energii o niskiej entropii w dwóch formach: zapasów i przepływów. Zapasy obejmują minerały ziem rzadkich, paliwa kopalne i inne złoża lądowe powstałe w wyniku złożonych, długotrwałych procesów zachodzących w ziemi przez tysiąclecia. Przepływy pochodzą z uznawanych za odnawialne źródeł, takich jak wiatr, woda i energia słoneczna, do których zalicza się również biomasę (jako pośrednie przedłużenie energii słonecznej). Ze względu na charakter każdego ze źródeł, zapasy są ograniczone ilościowo, podczas gdy przepływy są ograniczone zarówno pod względem tempa, jak i ilości. Cywilizacje, podobnie jak organizmy, mają metabolizm. Przetwarzają energię.

Rewolucja przemysłowa po raz pierwszy przeniosła pierwotny wkład energii w gospodarkę z przepływów na ziemskie zapasy. Pługi konne i żagle napędzane wiatrem, dwie formy pracy zależne od przepływów, zostały zastąpione przez zmechanizowane rolnictwo i statki napędzane parą, które opierają się na paliwach kopalnych. Skapitalizowaliśmy uśpioną energię słoneczną, skamieniałą przez miliony lat, aby uwolnić cywilizację od ograniczeń biologicznych przepływów ziemskich i stworzyć gwałtowny wzrost populacji i PKB.
Pomimo niezaprzeczalnych korzyści ekonomicznych i materialnych tej zmiany, miała ona efekt uboczny w postaci przyspieszenia procesu entropii i zwiększenia nieporządku w systemie klimatycznym. Chociaż całkowita ilość energii pozostaje niezmieniona w procesie gospodarczym (z wyjątkiem energii słonecznej), wydobycie minerałów i zużycie paliw kopalnych niezbędnych w procesie produkcji charakteryzuje zmiana jakościowa, która przenosi energię z porządku do nieładu. W ten sposób entropia stanowi podstawę niedoboru, ponieważ ludzie nie mogą przenieść energii w drugą stronę, ze stanu nieuporządkowania do uporządkowania; bez entropii byłoby fizycznie możliwe przekształcenie atmosferycznego CO2 z powrotem w bryłę węgla, tak samo jak możliwe byłoby przechwycenie i ponowne skonfigurowanie cząsteczek gumy utraconych podczas degradacji opony na chodniku.

Na koniec dnia, nasza gospodarka używa rzeczy i energii. Nawet jeśli pieniądze, nasza reprezentacja wartości, krążą po gospodarce w nieskończoność, dobra fizyczne, które reprezentują, podlegają prawu entropii. Obecny system ekonomiczny jest jak organizm, który rośnie w nieskończoność. Nasze serce pompuje krew i utrzymuje nas przy życiu, ale z czasem ta siła zużywa nasze komórki. Starzejemy się i degradujemy.
Więc jak entropia odnosi się do nauki o danych?
Teraz przyjrzeliśmy się, jak entropia odnosi się do energii, spójrzmy, jak odnosi się do komunikacji i Teorii Informacji. Myślę, że ten fragment biografii Claude’a Shannona, A Mind at Play, autorstwa Jimmy’ego Soni i Roba Goodmana, jest świetną anegdotyczną opowieścią o początkach entropii:
Shannon zwrócił się do wielkiego człowieka ze swoją ideą informacji-jako rozwiązanej niepewności – która miała stać się sercem jego pracy – i z nieeleganckim pytaniem. Jak powinien nazwać tę rzecz? Von Neumann odpowiedział od razu: „powiedzmy, że informacja zmniejsza 'entropię’. Po pierwsze, jest to dobre, solidne słowo z dziedziny fizyki. A co ważniejsze – kontynuował – nikt nie wie, czym tak naprawdę jest entropia, więc w debacie zawsze będziesz miał przewagę.”

Przed zajęciem się definicją entropii Shannona, pomocne może być rozbicie jego definicji informacji. Podstawowym założeniem teorii Shannona jest to, że wartość informacyjna przekazywanego komunikatu zależy od stopnia, w jakim treść komunikatu jest zaskakująca. Doskonałym przykładem tego w praktyce jest wykorzystanie częstotliwości występowania liter w języku. Z probabilistycznego punktu widzenia, jeśli wystąpienie litery jest jednym zdarzeniem, to najbardziej prawdopodobny wynik każdego danego zdarzenia ma taki rozkład prawdopodobieństwa:
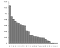
Im więcej jest liter, tym mniejsza jest niepewność w komunikacie. Ale zależy to również od rzadkości występowania danej litery. Na przykład, która z następujących wiadomości zawiera więcej informacji, 1 czy 2?
_AT
Opcja „1” zawiera dwie litery o stosunkowo wysokim prawdopodobieństwie, gdzie można przeliterować wszystkie rodzaje słów, wypełniając brakującą literę: „Bat”, „Cat”, „Hat”, „Fat”, „Sat”, itp. Opcja 2 zawiera stosunkowo nieuchwytny literę „H”, który ma kilka pozostałych opcji słowo jak „Hat” lub „Hit”, ale nie tak wiele jak opcja 1. Therefore, Opcja 2 komunikuje więcej informacji, ponieważ zmniejsza niepewność w większym stopniu.
Więc jeśli informacja jest rozwiązana niepewność, entropia musi być niepewność potrzeba rozwiązywania. Rzadkość zdarzenia, lub jego „niespodzianka”, określa jego zawartość informacyjną (jeśli kiedykolwiek grałeś w Scrabble, wiedziałbyś jak ograniczone byłyby opcje, gdybyśmy wylosowali literę „Q”). Za każdym razem, gdy przekazujemy kawałek informacji, ogólna entropia, nieporządek, niepewność, czy jakkolwiek chcesz to nazwać, zmniejsza się o proporcjonalną ilość lub tempo. Więc jaka jest ta proporcjonalna ilość?
Shannon obliczył, że miarą entropii informacji związanej z każdą możliwą wartością danych jest ujemny logarytm funkcji masy prawdopodobieństwa dla tej wartości:
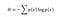
Entropia mierzy oczekiwaną ilość informacji przekazywanych przez identyfikację wyniku zdarzenia losowego, gdzie możliwe wyniki są funkcją prawdopodobieństwa. Wynika z tego, że rzut kością ma wyższą entropię niż rzut monetą, ponieważ każdy wynik rzutu kością (⅙) ma mniejsze prawdopodobieństwo niż wyrzucenie reszki lub główki (½). Graficzne spojrzenie na tę zależność pomaga:

Przekazując wynik reszka, wiemy, że reszka nie wystąpiła.
W uczeniu maszynowym, matematyczna interpretacja entropii jest używana do obliczania metryki przyrostu informacji dla wielu algorytmów. Drzewa decyzyjne, na przykład, wybierają jeden z wielu różnych atrybutów, znanych również jako cechy lub zmienne niezależne, aby wielokrotnie podzielić próbki na podzbiory. Przy każdym podziale, algorytm wybiera jeden atrybut do podziału próbki i kontynuuje to do momentu, gdy wszystkie podzbiory są czyste, lub innymi słowy, każda pojedyncza próbka w podzbiorze ma tę samą klasyfikację lub wartość docelową.
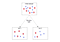
Aby zmierzyć czystość podzbioru próbki, algorytm potrzebuje miary ilościowej, aby obiektywnie wybrać cechę, na podstawie której należy dokonać podziału w każdym danym węźle. Tu właśnie wkracza entropia. Na każdym etapie algorytm oblicza, która cecha wykaże największy przyrost informacji, a następnie decyduje o podziale. Oblicza również oczekiwany spadek niepewności przed i po podziale; jeśli się zmniejszy, podział zostaje zachowany, a algorytm przechodzi do następnego kroku. Jeśli nie zmalała, to znaczy, że algorytm osiągnął czystość i zatrzymuje się. W ten sposób jest odpowiedzialny zarówno za wybór cechy do podziału, jak i za zatrzymanie procesu.
Czy istnieje związek między termodynamiką a Teorią Informacji?
Entropia nieubłaganie przepływa przez drzewo decyzyjne, tak jak nieubłaganie przepływa przez filiżankę kawy w powietrze. W energetyce maszeruje do równowagi termodynamicznej; w teorii informacji maszeruje do czystości.
W swoim rdzeniu energetyczna interpretacja entropii i interpretacja entropii w teorii informacji zbiegają się w tym samym punkcie – w fundamentalnych prawach fizyki. Komunikacja wymaga energii, a wykorzystanie energii wymaga komunikacji. Według Shannona, wartość entropii fragmentu informacji stanowi absolutne ograniczenie najkrótszej możliwej średniej długości wiadomości lub tego, jak bardzo można ją skompresować bez utraty informacji w trakcie jej przesyłania. Półprzewodniki, latarki i stukanie w patelnię alfabetem Morse’a wymaga ludzkiej energii, a nasza komunikacja zawsze będzie dążyć do najbardziej efektywnych środków przekazu.
W energii staramy się zminimalizować entropię poprzez ograniczenie tego, ile zużywamy i jak efektywnie to zużywamy. Naszym celem jest znalezienie uporządkowanych źródeł energii i oparcie się wpływowi entropii na nasze ciała. W komunikacji minimalizujemy entropię poprzez znajdowanie informacji i zmniejszanie niepewności. W pewnym sensie, poprzez zmniejszenie nieporządku poprzez komunikację, możemy zatrzymać entropijny proces energii; łowca-zbieracz może używać języka do komunikowania się z innym, aby ostrzec przed pożarciem przez lwa, zarówno zmniejszając niepewność 1. gdzie jest lew (entropia informacji) i 2. procesu bycia pożartym przez lwa (entropia energii). Ten akt komunikowania się zmniejsza przestrzeń prawdopodobieństwa wszystkich możliwych zdarzeń i pozwala nam działać bardziej efektywnie i skutecznie. Zrozumienie natury działania tego potężnego prawa w sferze cyfrowej i fizycznej jest kluczem do zrozumienia powiązań między termodynamiką a erą informacji.




