Metoda dzielenia syntetycznego
Muszę powiedzieć, że dzielenie syntetyczne jest najbardziej „zabawnym” sposobem dzielenia wielomianów. Ma mniej kroków, aby dojść do odpowiedzi w porównaniu do metody długiego dzielenia wielomianów. W tej lekcji przejdę przez pięć (5) przykładów, które, mam nadzieję, powinny zaznajomić Cię z podstawowymi procedurami w pomyślnym dzieleniu wielomianów przy użyciu dzielenia syntetycznego.
Rzeczy do zapamiętania:
- Upewnij się, że dywidenda jest w formie standardowej. Oznacza to, że potęgi są w kolejności malejącej.
- Dzielnik musi być w postaci x – lewa strona( c prawa strona).
Przykłady dzielenia wielomianów za pomocą dzielenia syntetycznego
Przykład 1: Podziel poniższy wielomian.
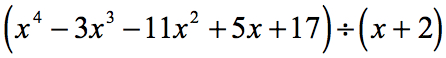
Przeanalizujmy ponownie podany problem i wprowadźmy niezbędne poprawki, jeśli to konieczne.
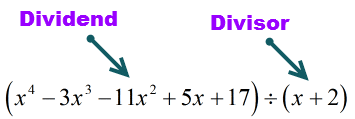
Działka (rzeczy do podzielenia) jest w postaci standardowej, ponieważ wykładniki są w kolejności malejącej. To dobrze!
Dzielnik musi być przepisany jako
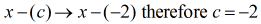
W tym momencie mogę teraz ustawić dzielenie syntetyczne poprzez wyodrębnienie współczynników dywidendy, a następnie wyłożenie ich na wierzch.
Bezpośrednio po lewej stronie, umieść wartość c = – 2 wewnątrz „pudełka”.
Na koniec, skonstruuj poziomą linię tuż poniżej współczynników dywidendy.
Kroki:
1. Zrzuć pierwszy współczynnik poniżej poziomej linii.
2. Pomnóż tę liczbę, którą zrzuciłeś, przez liczbę w „pudełku”. Niezależnie od jej iloczynu, umieść go nad poziomą linią tuż poniżej drugiego współczynnika.
3. Dodaj kolumnę liczb, a następnie umieść sumę bezpośrednio poniżej poziomej linii.
4. Powtarzaj ten proces, aż skończą Ci się kolumny do dodania.
Zobacz animowane rozwiązanie poniżej:
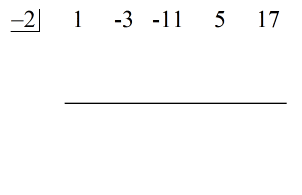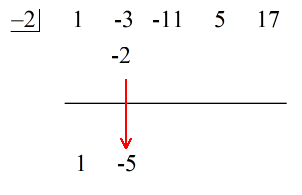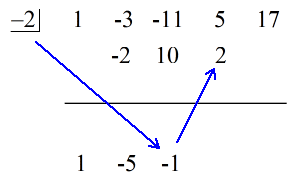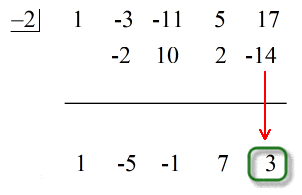
Ostatnia liczba poniżej poziomej linii jest zawsze resztą! Reszta tego zadania wynosi 3.
Więc jak przedstawimy naszą ostateczną odpowiedź?
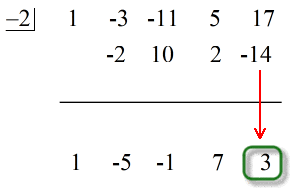
- Przedstaw ostateczną odpowiedź w postaci
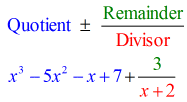
Zauważ, że liczby poniżej linii poziomej z wyjątkiem ostatniej (reszta) są współczynnikami ilorazu.
Więcej, wykładniki zmiennych ilorazu są wszystkie zmniejszone o 1.
Przykład 2: Podziel wielomian.
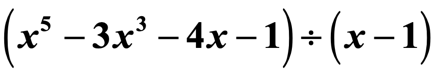
To nie jest podchwytliwe pytanie. Zauważ, że w ilorazie nie ma wszystkich wykładników zmiennej x.
Widzę, że brakuje nam {x^4} i {x^2}. Aby uwzględnić wszystkie współczynniki zmiennej x w malejących potęgach, powinniśmy przepisać oryginalny problem w ten sposób. Dołącz zera do tych brakujących x. Również wyrazić dzielnik jako x – (c), co jasno ujawnia wartość c, czyli c = + 1.
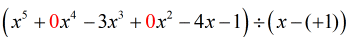
Z tego punktu mogę teraz ustawić liczby, aby kontynuować proces.
Kroki:
1. Zrzuć pierwszy współczynnik poniżej linii poziomej.
2. Pomnóż tę liczbę, którą zrzuciłeś, przez liczbę w „pudełku”. Niezależnie od jego iloczynu, umieść go powyżej poziomej linii tuż poniżej drugiego współczynnika.
3. Dodaj kolumnę liczb, a następnie umieść sumę bezpośrednio poniżej poziomej linii.
4. Powtarzaj proces, aż zabraknie kolumn do dodania.
Zobacz animowane rozwiązanie poniżej:
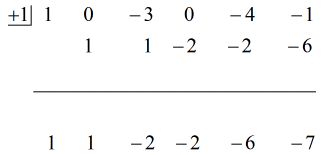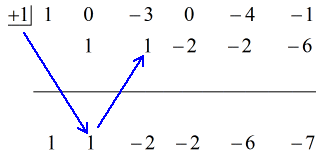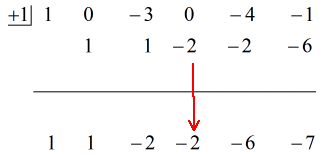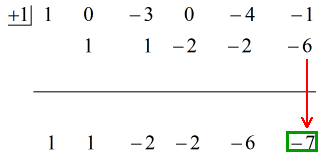
Składając więc ostateczną odpowiedź w postaci
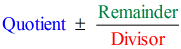
mamy
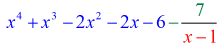
Przykład 3: Podziel poniższy wielomian.
Lewy( { – 2{x^4} + x} \prawy)
To staje się coraz ciekawsze! Iloraz zdecydowanie wygląda okropnie, ponieważ wiele mu brakuje. Nie tylko brakuje mu kilku x, którymi są {x^3} i {x^2}, ale również nie ma stałej.
Aby to naprawić, przepiszę oryginalny problem w taki sposób, aby wszystkie x były uwzględnione. Ale co ważniejsze, nie zapomnij uwzględnić brakującej stałej, która jest równa zero.
„Nowy i poprawiony” problem powinien wyglądać tak:
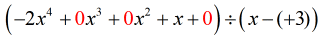
Od tego miejsca wykonaj kroki jak zwykle.
Kroki:
1. Zrzuć pierwszy współczynnik poniżej poziomej linii.
2. Pomnóż tę liczbę, którą zrzucasz, przez liczbę w „pudełku”. Niezależnie od jego iloczynu, umieść go powyżej poziomej linii tuż poniżej drugiego współczynnika.
3. Dodaj kolumnę liczb, a następnie umieść sumę bezpośrednio poniżej poziomej linii.
4. Powtarzaj proces, aż zabraknie kolumn do dodania.
Zobacz animowane rozwiązanie poniżej:
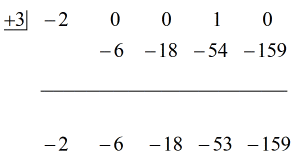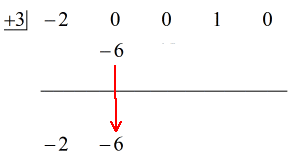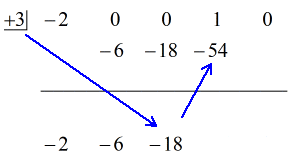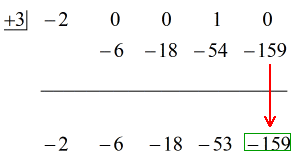
Okay then, the final answer for this is
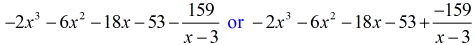
Ostatnią odpowiedź możesz zapisać na dwa sposoby. Pierwszym z nich jest użycie symbolu minus lub odejmowania, aby wskazać, że reszta jest ujemna. Drugi to użycie symbolu +, ale dołączenie symbolu ujemnego do licznika. Oznaczają one to samo!
Przykład 4: Podziel poniższy wielomian.
Lewa strona( { – {x^5} + 1} \prawa)
Nie zniechęcaj się tym problemem. To jest właściwie dość łatwe, zwłaszcza teraz, gdy przeszedłeś już przez kilka przykładów. Zawsze pamiętaj o „uzupełnianiu brakujących części”, prawda?
Obserwuj dywidendę i powinieneś się zgodzić, że brakujące części to {x^4}, {x^3}, {x^2} i x.
Napisując ponownie oryginalny problem, który jest gotowy do dzielenia syntetycznego, otrzymujemy…
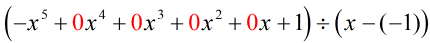
Wypełniliśmy brakujące x zerami i jednoznacznie rozwiązujemy dla c = -1.
Kroki:
1. Zrzuć pierwszy współczynnik poniżej linii poziomej.
2. Pomnóż tę liczbę, którą zrzucasz, przez liczbę w „pudełku”. Niezależnie od jego iloczynu, umieść go nad linią poziomą tuż poniżej drugiego współczynnika.
3. Dodaj kolumnę liczb, a następnie umieść sumę bezpośrednio pod linią poziomą.
4. Powtarzaj ten proces, aż zabraknie Ci kolumn do dodania.
Zobacz animowane rozwiązanie poniżej:
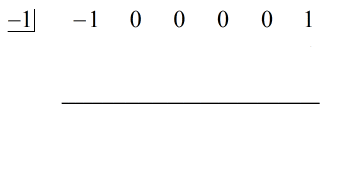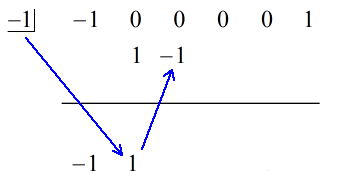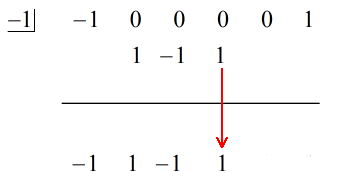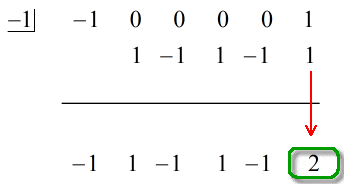
Ostatnia liczba poniżej poziomej linii zawsze będzie resztą. Nie zapomnij o tym. W tym przypadku reszta jest równa 2.
Naszą ostateczną odpowiedzią jest
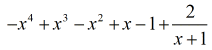
Przykład 5: Podziel wielomian przez dwumian.
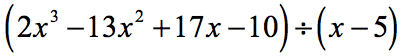
W tym przykładzie otrzymamy resztę równą zero. Kiedy tak się dzieje, dzielnik staje się czynnikiem dywidendy. Innymi słowy, dzielnik równo dzieli dywidendę.
Badając problem, widzę, że nie ma żadnych brakujących elementów. Wszystkie potęgi x są uwzględnione i mamy stałą. To świetnie! Ten problem jest w rzeczywistości gotowy do dzielenia syntetycznego.
Kroki:
1. Zrzuć pierwszy współczynnik poniżej poziomej linii.
2. Pomnóż tę liczbę, którą zrzuciłeś, przez liczbę w „pudełku”. Niezależnie od jego iloczynu, umieść go powyżej linii poziomej tuż poniżej drugiego współczynnika.
3. Dodaj kolumnę liczb, a następnie umieść sumę bezpośrednio poniżej linii poziomej.
4. Powtarzaj proces, aż zabraknie kolumn do dodania.
Zobacz animowane rozwiązanie poniżej:
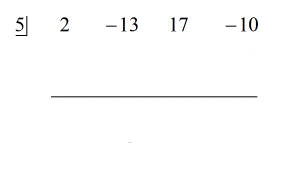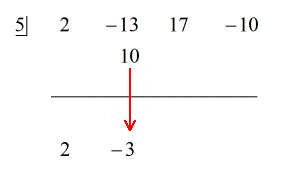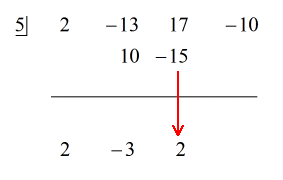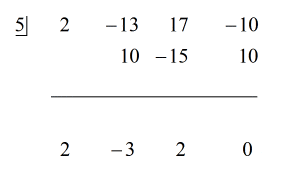
Ponieważ reszta jest równa zero, oznacza to, że dzielnik x – 5 jest współczynnikiem dywidendy
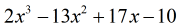
therefore
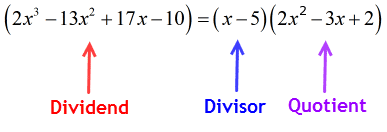
Praktyka z arkuszami
Może Cię również zainteresować:
Dodawanie i odejmowanie wielomianów
Dzielenie wielomianów metodą długiego dzielenia
Mnożenie dwumianów metodą FOIL
Mnożenie wielomianów
.




