Powierzchnia Cylindra – Wyjaśnienie & Przykłady
Zanim wskoczymy do tematu powierzchni cylindra, przejrzyjmy cylinder. W geometrii, cylinder jest trójwymiarową figurą z dwoma okrągłymi podstawami równoległymi do siebie i zakrzywioną powierzchnią.
How to Find the Surface Area of a Cylinder?
Powierzchnia cylindra jest sumą dwóch równoległych i przystających okrągłych twarzy i zakrzywionej powierzchni.
Ten artykuł omówi, jak znaleźć całkowitą powierzchnię i powierzchnię boczną cylindra.
Aby obliczyć pole powierzchni cylindra, musisz znaleźć powierzchnię podstawy (B) i zakrzywioną powierzchnię (CSA). Dlatego pole powierzchni lub całkowita powierzchnia cylindra jest równa sumie pola podstawy razy dwa i pola powierzchni zakrzywionej.
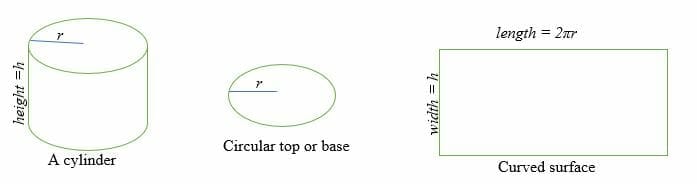
Powierzchnia zakrzywiona cylindra jest równa prostokątowi, którego długość wynosi 2πr, a szerokość h.
Gdzie r = promień okrągłej powierzchni i h = wysokość cylindra.
Powierzchnia zakrzywiona = Pole prostokąta =l x w = πdh
Powierzchnia podstawy, B = Pole koła = πr2
Wzór na pole powierzchni walca
Wzór na pole powierzchni całkowitej walca jest dany jako:
Całkowite pole powierzchni walca = 2πr2 + 2πrh
TSA = 2πr2 + 2πrh
Gdzie 2πr2 jest polem powierzchni czołowej okręgu górnego i dolnego, a 2πrh jest polem powierzchni zakrzywionej.
Biorąc 2πr jako wspólny czynnik z RHS, otrzymujemy;
TSA = 2πr (h + r) ……………………………………. (Wzór na pole powierzchni walca)
Rozwiążmy przykładowe zadania dotyczące pola powierzchni walca.
Przykład 1
Znajdź pole powierzchni całkowitej walca, którego promień wynosi 5 cm, a wysokość 7 cm.
Rozwiązanie
Zgodnie ze wzorem,
TSA = 2πr (h + r)
= 2 x 3.14 x 5(7 + 5)
= 31,4 x 12
= 376,8 cm2
Przykład 2
Znajdź promień walca, którego pole powierzchni całkowitej wynosi 2136,56 stóp kwadratowych, a wysokość jest równa 3 stopy.
Rozwiązanie
Dane:
TSA = 2136.56 stóp kwadratowych
Wysokość, h = 3 stopy
Ale, TSA = 2πr (h + r)
2136.56 =2 x 3.14 x r (3 + r)
2136.56 = 6.28r (3 + r)
Dzięki własności dystrybucyjnej mnożenia na RHS mamy,
2136,56 = 18,84r + 6,28r2
Podziel każdy z członów przez 6,28
340.22 = 3r + r2
r2 + 3r – 340,22 = 0 ……… (równanie kwadratowe)
Rozwi±zuj±c równanie za pomoc± wzoru kwadratowego, otrzymujemy,
r = 17
Więc promień walca wynosi 17 stóp.
Przykład 3
Koszt pomalowania cylindrycznego pojemnika wynosi 0,04$ za cm2. Znajdź koszt pomalowania 20 pojemników o promieniu, 50 cm, i wysokości, 80 cm.
Rozwiązanie
Oblicz całkowitą powierzchnię 20 pojemników.
TSA = 2πr (h + r)
= 2 x 3.14 x 50 (80 + 50)
= 314 x 130
= 40820 cm2
Całkowita powierzchnia 20 pojemników = 40 820 cm2 x 20
=816 400 cm2
Koszt malowania = 816 400 cm2 x 0$.04 za cm2
= 32 656$.
Więc koszt pomalowania 20 pojemników wynosi 32 656$.
Przykład 4
Znajdź wysokość walca, jeśli jego powierzchnia całkowita wynosi 2552 in2, a promień 14 in.
Rozwiązanie
Dane:
TSA = 2552 in2
Promień, r = 14 in.
Ale, TSA = 2πr (h + r)
2552 = 2 x 3.14 x 14 (14 + h)
2552 = 87,92(14 + h)
Podziel obie strony przez 87,92, aby otrzymać,
29.026 = 14 + h
Odejmij przez 14 po obu stronach.
h = 15
Więc wysokość cylindra wynosi 15 in.
Powierzchnia boczna cylindra
Jak stwierdzono wcześniej, powierzchnia zakrzywionej powierzchni cylindra jest tym, co określa się mianem powierzchni bocznej. Mówiąc prościej, pole powierzchni bocznej walca jest to pole powierzchni walca z wyłączeniem powierzchni podstawy i dna (powierzchni kołowej).
Wzór daje pole powierzchni bocznej walca;
LSA = 2πrh
Przykład 5
Znajdź pole powierzchni bocznej walca, którego średnica wynosi 56 cm, a wysokość 20 cm.
Rozwiązanie
Dane:
Średnica = 56 cm, stąd promień, r =56/2 = 28 cm
Wysokość, h = 20 cm
Zgodnie ze wzorem,
LSA = 2πrh
= 2 x 3.14 x 28 x 20
= 3516,8 cm2.
Więc, pole powierzchni bocznej walca wynosi 3516,8 cm2.
Przykład 6
Powierzchnia boczna walca wynosi 144 ft2. Jeżeli promień walca jest równy 7 stóp, to znajdź wysokość walca.
Rozwiązanie
Dane;
LSA = 144 ft2
Promień, r = 7 stóp
.




