Prawdopodobieństwo Wprowadzenie: Artykuły i filmy z rozwiązaniami!

admin 0 Comments Articles

Prawdopodobieństwo Wprowadzenie: Artykuły i filmy z rozwiązaniami!

Rolka w kości, znalezienie miejsca parkingowego, wygrana w karty; To tylko niektóre sytuacje, w których możesz chcieć znaleźć prawdopodobieństwo wystąpienia zdarzenia. Jeśli chcesz wiedzieć, jak znaleźć prawdopodobieństwo, musisz najpierw dowiedzieć się, jaki rodzaj pytania masz. Na przykład, jak znaleźć prawdopodobieństwo zajścia zdarzenia jest inne niż znalezienie prawdopodobieństwa, że członkowie grupy wybiorą tę samą rzecz.

Niektóre prawdopodobieństwa są łatwe do określenia, jak na przykład prawdopodobieństwo rzucenia kostką lub wybrania z talii kart.

Pytania, które dotyczą twierdzenia dwumianowego są również łatwe do zidentyfikowania. W tego typu eksperymentach, jedynymi możliwymi wynikami są „Sukces” lub „Porażka”: jak tak/nie, głowa/ogon lub czarne/białe.

Inne typy pytań, które możesz napotkać, dotyczą ludzi, jak:

• Wybór osoby z grupy lub komitetu.
• Prawdopodobieństwo, że grupa wybierze tę samą rzecz.

Zdarzenia

Czy chcesz znaleźć prawdopodobieństwo zajścia prostego zdarzenia? Na przykład padającego deszczu lub znalezienia miejsca parkingowego w centrum miasta? Zobacz:
Prawdopodobieństwo zajścia prostego zdarzenia.
Z drugiej strony, jeśli chcesz czegoś zupełnie przeciwnego, zobacz:
Jak znaleźć prawdopodobieństwo zajścia zdarzenia NIE.

Czy twoje pytanie dotyczy zajścia jednego zdarzenia, biorąc pod uwagę inne zdarzenie? Jak szanse na znalezienie miejsca parkingowego, biorąc pod uwagę, że jest to dzień gry, lub znalezienie pewnej popularnej zabawki w Czarny Piątek? Jeśli tak, sprawdź:

• Szanse wystąpienia zdarzenia, biorąc pod uwagę inne zdarzenie.
• Dwa zdarzenia występujące razem.

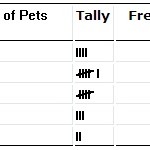
Tabela rozkładu częstości.

Rozkłady częstości

Czy masz rozkład częstości, z którym możesz pracować? A może jesteś w stanie stworzyć tabelę rozkładu częstości z podanymi danymi? Na przykład, masz x ilość przedmiotów z pewną cechą. Probability frequency distribution.

Introduction to Probability: How-to Articles and Videos.

1. Permutations and Combinations: How to Solve Problems
2. Problemy z prawdopodobieństwem: Rozwiąż je w łatwy sposób!
3. Prawdopodobieństwo a i b.
4. Reguła prawdopodobieństwa całkowitego.
5. Twierdzenie Bayesa: Easy Solution Steps.
6. Prior Probability (including Uninformative and Conjugate).
7. How to Make a Probability Distribution from data.
8. How to find the Probability of Selecting a Person from a Group or Committee.
9. Jak znaleźć prawdopodobieństwo zdarzenia, które NIE wystąpi.
10. Rozkład częstości prawdopodobieństwa.
11. Jak znaleźć prawdopodobieństwo wystąpienia prostego zdarzenia.
12. Zdarzenie losowe: Probability Given a Percentage.
13. How to Find the Probability of Group Members Choosing the Same Thing.
14. How to find the Probability of Two Dependent Events Occurring Together.
15. How to find the Probability of an Event Occurring, Given Another Event.
16. Jak użyć drzewa prawdopodobieństwa do obliczenia prawdopodobieństwa.
17. Jak znaleźć prawdopodobieństwo wyciągnięcia karty z talii.
18. Jak sprawdzić, czy coś jest zdarzeniem wzajemnie wykluczającym się.
19. Jak odróżnić zdarzenia zależne od niezależnych.
20. Prawdopodobieństwo: Dice Rolling.
21. How to Draw a Venn diagram.
22. How to Create an Euler Diagram.
23. 5 choose 3: how to solve combinations.
24. How to use the fundamental counting principle.
25. How to find expected value for a discrete random variable.

Introduction to Probability: Definicje

• Prawdopodobieństwo aksjomatyczne.
• Prawo Benforda
• Co to jest eksperyment dwumianowy?
• Stopy bazowe i fałsz stopy bazowej
• Wyniki Briera
• Wyczerpanie zbiorowe
• Co to są kombinacje?
• Zdarzenia komplementarne.
• Oczekiwanie warunkowe
• Co to jest warunkowa częstość względna?
• Przeliczalna addytywność
• Zbiór pusty
• Prawdopodobieństwo epistemiczne
• Przestrzenie zdarzeń.
• Co to jest prawdopodobieństwo doświadczalne?
• Współczynnikowe rozkłady prawdopodobieństwa.
• Rozkład graniczny.
• Maximum Likelihood Estimation
• Memoryless Property.
• Monte Carlo Method.
• Monty Hall Problem
• What is a Mutually Exclusive Event?
• What is a Mutually Inclusive Events?
• Zdarzenia wzajemnie niezależne i parami niezależne.
• Co to jest reguła mnożenia?
• Nash Equilibrium
• Zbiór niepusty
• Zadania praktyczne dotyczące prawdopodobieństwa normalnego.
• Co to jest normalny wykres prawdopodobieństwa?
• Prawdopodobieństwo obiektywne
• Co to jest iloraz szans?
• Analiza predykcyjna
• Co to jest tabela rozkładu prawdopodobieństwa?
• Miara prawdopodobieństwa
• Co to jest przestrzeń prawdopodobieństwa?
• Wektory prawdopodobieństwa
• Co to są przestrzenie próbkowania?
• Modele stochastyczne.
• Co to jest prawdopodobieństwo subiektywne?
• Co to jest prawdopodobieństwo teoretyczne?
• Co to jest model urnowy?

Kalkulatory.

• Kalkulator permutacji i kalkulator kombinacji online.

Formuły prawdopodobieństwa / Reguły prawdopodobieństwa

Jedną z najbardziej niewygodnych rzeczy, których studenci nie lubią w formułach, jest ich brak w prawdopodobieństwie i statystyce. Istnieje kilka zszywek, w tym kilka obowiązkowych notacji:

Zakres prawdopodobieństwa
0 ≤ P(A) ≤ 1
To stwierdza, że prawdopodobieństwo zdarzenia jest gdzieś pomiędzy zerem a 100% (w systemie dziesiętnym, to jest 0 i 1). Będziesz chciał zapamiętać tę regułę podczas dodawania lub mnożenia prawdopodobieństw zdarzeń. Jeśli twoja odpowiedź jest powyżej 100%, to jest to wskazówka, że mogłeś zrobić coś źle.

Reguła zdarzeń komplementarnych
P(AC) + P(A) = 1
Zdarzenia komplementarne zdarzają się, gdy są tylko dwa wyniki, jak rzucanie monetą. Rzucanie kością by sprawdzić czy dostaniemy szóstkę jest również komplementarne; jedyne dwa wyniki to otrzymanie szóstki (1/6 szansy) lub nie otrzymanie szóstki (5/6 szansy). Te dwa prawdopodobieństwa muszą się sumować do 1.
Możesz również zobaczyć ten wzór zapisany w ten sposób:
p(A) + p(A’) = 1
który może być przekształcony algebraicznie do postaci:
p(A’) = 1 – p(A).
Wszystkie trzy wzory są równoważne: to, która terminologia (A’ czy Ac) jest używana zależy od autora podręcznika i nauczyciela. Osobiście preferuję A’, które nazywam „nie A”. Prawdopodobieństwo „nie A”, jak sądzę, jest łatwiejsze do zrozumienia niż „dopełnienie” (albo zdarzenie się wydarzy, albo nie).

Reguła dodawania
P(A∪B) = P(A) + P(B) – P(A∩B)
gdzie ∪ jest związkiem, a ∩ przecięciem.
Co to mówi (po angielsku!) jest prawdopodobieństwo wystąpienia zdarzenia A LUB zdarzenia B (lub obu w tym samym czasie) jest:

• Prawdopodobieństwo wystąpienia zdarzenia A na własną rękę,
• Plus prawdopodobieństwo wystąpienia zdarzenia B na własną rękę,
• Plus prawdopodobieństwo wystąpienia obu zdarzeń w tym samym czasie.

Jeśli mamy zdarzenia wzajemnie się wykluczające, to P(A∩B) nie może zajść (zdarzenia nie mogą zajść razem), więc wzór staje się:
P(A∪B) = P(A)+P(B)- 0 = P(A)+P(B)

Zdarzenia rozłączne
Zdarzenia A i B są rozłączne, jeśli:
P(A∩B) = 0
Jest to po prostu inny sposób powiedzenia, że zdarzenia wzajemnie się wykluczają. Nie mogą one wystąpić w tym samym czasie.

Pokrewną formułą jest P((A∪B)c) lub, równoważnie ((A∪B)’). W języku angielskim mówi to „not the union”. Aby to rozwiązać, należy obliczyć unię i odjąć wynik od 1 (ponieważ prawdopodobieństwo zajścia lub nie zajścia zdarzeń musi sumować się do 1).

Prawdopodobieństwo warunkowe
P(A|B) = P(A∩B) / P(B)
Symbol „|” oznacza „biorąc pod uwagę, że”. Innymi słowy, prawdopodobieństwo zajścia zdarzenia B przy założeniu, że zajdzie zdarzenie A. Aby zobaczyć przykłady użycia wzoru, zobacz: prawdopodobieństwo warunkowe.

Formuła Bayesa
P(A|B) = P(B|A) – P(A) / P(B)
Twierdzenie Bayesa jest sposobem na obliczenie prawdopodobieństwa warunkowego, chociaż jest nieco bardziej zniuansowane. W skrócie, daje ono rzeczywiste prawdopodobieństwo zdarzenia, biorąc pod uwagę informacje o testach. Na przykład, jakie jest prawdopodobieństwo, że masz raka, jeśli twój test medyczny jest pozytywny (odpowiedź = dużo niższa niż myślisz). Aby zobaczyć kilka przykładów, zobacz: Bayes Theorem Examples i Posterior Distributions / Posterior Probabilities.

Zdarzenia niezależne
Zdarzenia A i B są niezależne, jeśli jedno z nich nie wpływa na prawdopodobieństwo drugiego. O zdarzeniach mówi się również, że są niezależne, jeśli prawdziwa jest następująca równość.
P(A∩B) = P(A) – P(B).
Równanie to wynika z reguły mnożenia, która mówi, że P(A∩B) = P(A) * P(B|A). Ponieważ wiemy, że P(B|A) = P(B) dla niezależnych zdarzeń, możemy zastąpić P(B|A) przez P(B), dając nam wzór.

Kilka uwag na temat reguł prawdopodobieństwa

Statystyka jest o szansach i rzutach piłką, a nie o absolutach i „właściwej odpowiedzi”. Wystarczy spojrzeć na dowolną ankietę Gallupa – rzadko są oni pewni więcej niż 90%, że mają „dobrą odpowiedź”. Istnieją techniki, których można użyć do obliczenia prawdopodobieństwa (jak mnożenie dwóch prawdopodobieństw razem, lub dodawanie ich). Jednak, poza być może dwumianową tabelą rozkładu i powyższymi wzorami (które w prawdziwym życiu nie są tak często używane), nie ma tak naprawdę żadnych wzorów prawdopodobieństwa, które można łatwo zastosować. Musisz powrócić do tej starej podstawówki, logiki (pamiętasz ją…była tam tuż przed tym jak zaczęli standardowo testować logikę z ciebie).

Trzy reguły formuł prawdopodobieństwa:

1. Nie ma żadnych reguł (cóż, bardzo niewiele, z wyjątkiem tych wymienionych powyżej).
2. Używaj logiki, nie równań.
3. Istnieje wiele, wiele różnych sposobów, aby dostać się do odpowiedzi – żaden z nich tak naprawdę nie używa formuł.

Oto pytanie, które przyszło do mojej skrzynki pocztowej dziś rano, które dotyczy prawdopodobieństwa:

„Jeśli próbowałbyś zebrać 6 kart baseballowych, które przyszły w paczkach ptysiów serowych, zakładając, że są one rozmieszczone równomiernie, ile paczek ptysiów serowych spodziewałbyś się kupić, zanim będziesz miał wszystkie 6 kart?”

Krokiem 1 do rozwiązania tego problemu jest uświadomienie sobie, że nie możesz szukać odpowiedzi w tabeli. Aby go rozwiązać, musisz myśleć jak dziecko.

Karta# 1:Masz 8 lat i idziesz do sklepu z pieniędzmi wystarczającymi na zakup jednej paczki serowych ptysiów. Masz nadzieję, że uda Ci się zebrać wszystkie 5 kart baseballowych, ale jeszcze ich nie masz. Jakie są szanse, że kupisz torbę i dostaniesz kartę, którą chcesz?

Odpowiedź, oczywiście, jest 100%. Kup pierwszą torbę, a masz 100% szans, że znajdzie się w niej karta, którą chcesz mieć.

Karta#2: Teraz sprawa robi się nieco trudniejsza. Wracasz do sklepu, aby dostać kartę#2. Ale jak już masz kartę # 1, Mickey Mantle. Nie chcesz go ponownie, ale jest 1/5 szansy, że go dostaniesz (a zatem 4/5 szansy, że nie dostaniesz). Ile torebek serowych ptysiów będziesz musiał kupić, aby zdobyć kartę nr 2, staje się problemem proporcji. Możesz to sobie wyobrazić w głowie, ale jeśli chcesz to wymodelować matematycznie, musisz ułożyć równanie. Jeśli jedna torebka serowych ptysiów daje 80% szans na zdobycie karty, którą chcesz zdobyć, ile torebek musisz kupić, aby uzyskać 100% szans?

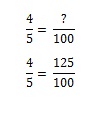
Aby uzyskać 100%, musisz kupić 1,25 torebki.

Karta#3:Szanse stają się coraz trudniejsze. Masz 60% szans na zdobycie trzeciej karty baseballowej i musisz kupić 1.667 worków, aby zdobyć tę trzecią kartę.

Karta# 4:Szanse zaczynają się robić trochę ponure. Masz 40% szans na zdobycie czwartej karty baseballowej i będziesz musiał kupić 2,5 torby, aby zdobyć tę trzecią kartę.

Karta# 5:Szanse są przeciw tobie. Masz 20% szans na zdobycie ostatniej karty i będziesz musiał kupić 5 worków, aby zdobyć tę trzecią kartę.

Więc całkowita ilość worków, które będziesz musiał kupić równa się:
1 + 1.25 + 1.667 + 2.5 + 5
Ale czekaj! (I tu pojawia się odrobina logiki). Nie możesz iść do sklepu i kupić 1,25 torebki serowych ptysiów, więc musisz zaokrąglić w górę. Równanie staje się:
1 + 2 + 2 + 3 + 5 = 13 torebek.

Jedna ważna uwaga dotycząca wzorów: pamiętaj, że nic nie jest absolutne. Jestem dość pewny, że gdybyś kupił 13 torebek serowych ptysiów i zakładając, że karty są równomiernie rozłożone, dostałbyś wszystkie 5 kart. Ale… prawdopodobieństwo jest o szansie, i to może być tylko twój pech, aby dostać tę samą kartę 10 razy z rzędu (pamiętam, że zdarzyło mi się to jako dziecko). Ale może być inne wyjaśnienie dla twojego „pecha”, a mianowicie, że firmy chcą, abyś kupił jak najwięcej torebek, więc postarają się, aby szanse działały na ich korzyść. Nawet jeśli karty są równomiernie rozłożone, firma może wysłać torby z kartami #1, #2 i #3 do jednego sklepu (w ten sposób zwabiając Cię, abyś zebrał więcej niż połowę kart), a #4 i #5 do innego sklepu.

Jakie inne sposoby, o których możesz pomyśleć, że producenci mogą obrócić szanse na swoją korzyść?

Prawdopodobieństwo, że grupa wybierze to samo

Pytania o prawdopodobieństwo można podzielić na różne typy. Kiedy jesteś proszony o znalezienie prawdopodobieństwa, że grupa wybierze to samo, rozważasz działania losowych członków grupy (może to być tak mała grupa jak komitet lub tak duża jak populacja Stanów Zjednoczonych).
Pytania o prawdopodobieństwo dają ci grupę i proszą cię o obliczenie prawdopodobieństwa wystąpienia zdarzenia dla pewnej liczby losowych członków tej grupy.

Prawdopodobieństwo, że grupa wybierze to samo: Kroki

Przykładowy problem: Na targach książki jest 200 osób. 159 z nich kupi co najmniej jedną książkę. Jeśli przebadamy 5 losowych osób wychodzących z targów, jakie jest prawdopodobieństwo, że wszystkie one kupią przynajmniej jedną książkę?

Jakie jest prawdopodobieństwo, że grupa kupi przynajmniej jedną książkę?

Krok 1: Przekształć dane w pytaniu na ułamek. Na przykład zdanie: „159 osób na 200” można przekształcić na: 159/200.

Krok 2: Pomnóż ułamek przez siebie. Powtarzaj dla dowolnej liczby losowo wybranych elementów (np. osób). W naszym przykładzie mamy 5 ankietowanych osób, więc chcemy:

159/200 x 159/200 x 159/200 x 159/200 x 159/200 = 0,3176
Tak znaleźć prawdopodobieństwo, że grupa wybierze tę samą rzecz!

Wskazówka: Może być łatwiej zamienić ułamek na dziesiętny przed pomnożeniem. W tym przypadku, 159/200 = 0,795.

Sprawdź nasz kanał YouTube po więcej pomocy i wskazówek dotyczących statystyki! Mamy filmy dla najczęstszych problemów, z którymi możesz się zetknąć. Plus filmy na temat używania Excela w statystyce > wszystko od robienia podstawowych wykresów słupkowych do rozwiązywania złożonych problemów z analizą danych.

——————————————————————————

Potrzebujesz pomocy z zadaniem domowym lub pytaniem testowym? Dzięki Chegg Study możesz uzyskać rozwiązania swoich pytań krok po kroku od eksperta w danej dziedzinie. Pierwsze 30 minut z korepetytorem Chegg jest bezpłatne!