Skewness – Quick Introduction, Examples & Formulas
Skewness to liczba, która wskazuje, w jakim stopniu
zmienna jest asymetrycznie rozłożona.
- Positive (Right) Skewness Example
- Negative (Left) Skewness Example
- Population Skewness – Formula and Calculation
- Sample Skewness -. Formula and Calculation
- Skewness in SPSS
- Skewness – Implications for Data Analysis
Positive (Right) Skewness Example
A scientist has 1,000 osób wypełniło pewne testy psychologiczne. Dla testu 5, wyniki testu mają skośność = 2.0. Histogram tych wyników jest pokazany poniżej.
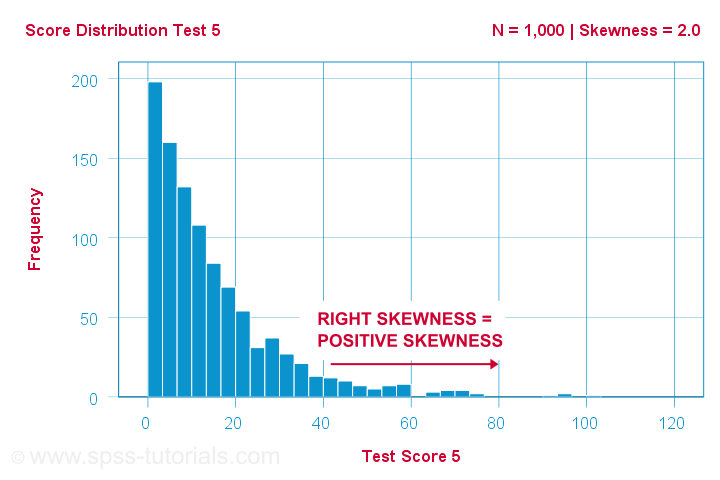
Histogram pokazuje bardzo asymetryczny rozkład częstości. Większość ludzi zdobywa 20 punktów lub mniej, ale prawy ogon rozciąga się do 90 lub więcej. This distribution is right skewed.
If we move to the right along the x-axis, we go from 0 to 20 to 40 points and so on. Więc w kierunku prawej strony wykresu, wyniki stają się bardziej pozytywne. Dlatego prawoskośność jest dodatnią skośnością, co oznacza skośność > 0. Ten pierwszy przykład ma skośność = 2,0, jak wskazano w prawym górnym rogu wykresu. Wyniki są silnie dodatnio skośne.
Negative (Left) Skewness Example
Inna zmienna – wyniki na teście 2 okazują się mieć skośność = -1.0. Ich histogram jest pokazany poniżej.

Większość wyników znajduje się pomiędzy 60 a 100 lub mniej więcej. Jednakże, lewy ogon jest nieco rozciągnięty. Więc ten rozkład jest lewoskośny.
Prawo: w lewo, w lewo. Jeśli podążymy za osią x w lewo, przesuniemy się w kierunku bardziej negatywnych wyników. To dlatego lewa skośność jest ujemną skośnością.I rzeczywiście, skośność = -1.0 dla tych wyników. Ich rozkład jest lewoskośny. Jednakże, jest on mniej skośny – lub bardziej symetryczny – niż nasz pierwszy przykład, który miał skośność = 2.0.
Symmetrical Distribution Implies Zero Skewness
Wreszcie, rozkłady symetryczne mają skośność = 0. Wyniki w teście 3 – mające skośność = 0.1- zbliżają się do tego.

Teraz, obserwowane rozkłady rzadko są dokładnie symetryczne. Jest to głównie widoczne dla niektórych teoretycznych rozkładów próbkowania. Niektóre przykłady to
- rozkład (standardowy) normalny;
- rozkład t i
- rozkład dwumianowy, jeśli p = 0.5.
Te rozkłady są wszystkie dokładnie symetryczne i dlatego mają skośność = 0.000…
Skośność populacji – wzór i obliczenia
Jeśli chciałbyś obliczyć skośność dla jednej lub więcej zmiennych, po prostu zostaw obliczenia jakiemuś oprogramowaniu. Ale – tylko dla kompletności – i tak podam wzory.
Jeśli twoje dane zawierają całą populację, oblicz skośność populacji jako:
$$Populacja = skośność = ^3}{N}$$
gdzie
- $(X_i) to każdy indywidualny wynik;
- (™mu} jest średnią populacji;
- (™sigma>) jest odchyleniem standardowym populacji i
- (N} jest liczebnością populacji.
Przykładowe obliczenia z użyciem tego wzoru można znaleźć w arkuszu Googlesheet (pokazanym poniżej).
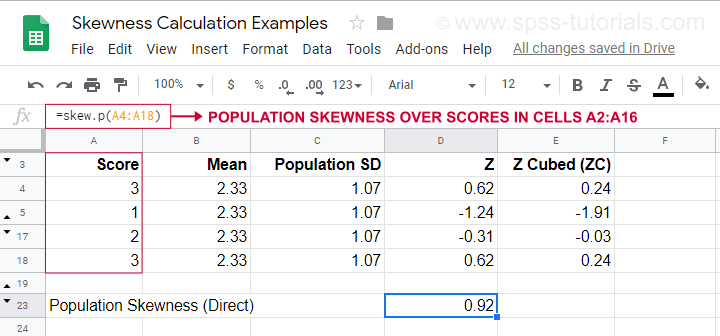
Pokazuje on również, jak uzyskać skośność populacji bezpośrednio za pomocą=SKEW.P(…)gdzie „.P” oznacza „populację”. Potwierdza to wynik naszych ręcznych obliczeń. Niestety, ani SPSS ani JASP nie obliczają skośności populacji: oba są ograniczone do skośności próbki.
Skośność próby – wzór i obliczenia
Jeśli twoje dane zawierają prostą próbę losową z jakiejś populacji, użyj
$Sample;skośność = ^3}{S^3(N – 1)(N – 2)}$$
gdzie
- Sigma(X_i – ^3) jest każdym indywidualnym wynikiem;
- (overline{X}}) jest średnią z próby;
- (S) jest odchyleniem standardowym z próby i
- (N) jest wielkością próby.
Przykładowe obliczenia są pokazane w tym arkuszu Googlesheet (pokazanym poniżej).
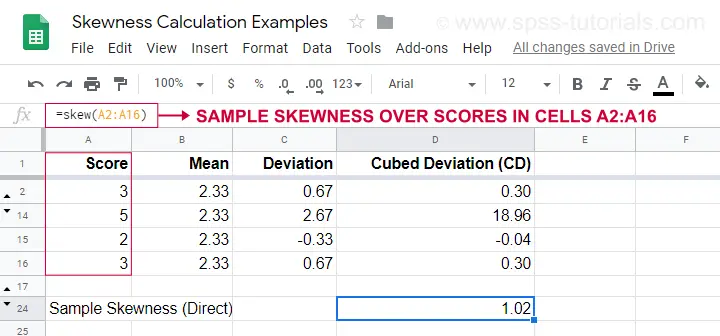
Łatwiejszą opcją uzyskania skośności próby jest użycie=SKEW(…).co potwierdza wynik naszych ręcznych obliczeń.
Skewness w SPSS
Po pierwsze, „skewness” w SPSS zawsze odnosi się do skewness próbki: po cichu zakłada, że twoje dane zawierają próbkę, a nie całą populację. Istnieje wiele opcji, aby ją uzyskać. Moim ulubionym jest MEANS, ponieważ składnia i dane wyjściowe są czyste i proste. Poniższe zrzuty ekranu poprowadzą Cię przez to.

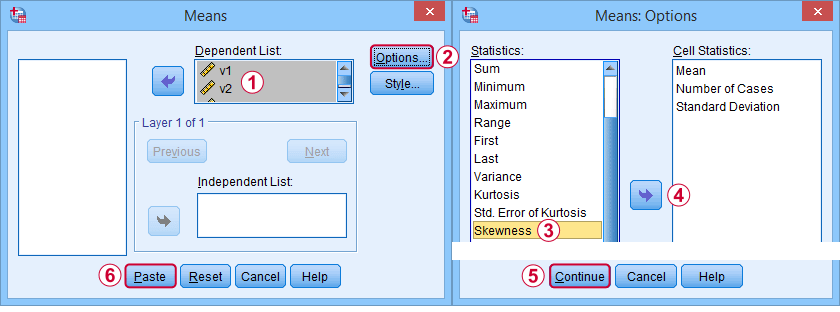
Składnia może być tak prosta, jakmeans v1 to v5
/cells skew.Bardzo kompletna tabela – zawierająca średnie, odchylenia standardowe, mediany i więcej – jest uruchamiana zmeans v1 to v5
/cells count min max mean median stddev skew kurt.Wynik jest pokazany poniżej.
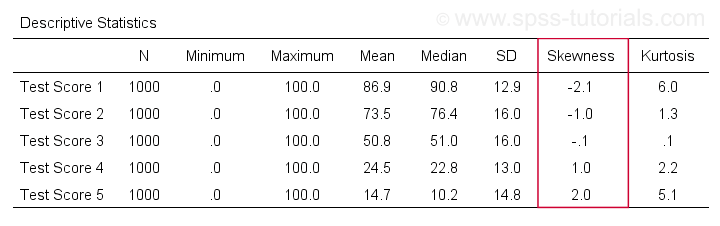
Skewness – Implications for Data Analysis
Wiele analiz -ANOVA, t-testy, regresja i inne- wymaga założenia normalności: zmienne powinny być normalnie rozłożone w populacji. Rozkład normalny ma skośność = 0. Tak więc obserwowanie znacznej skośności w niektórych danych próbki sugeruje, że założenie normalności jest naruszone.
Takie naruszenia normalności nie stanowią problemu dla dużych rozmiarów próbek – powiedzmy N > 20 lub 25 lub tak. W tym przypadku, większość testów jest odporna na takie naruszenia. Wynika to z centralnego twierdzenia granicznego. Krótko mówiąc, dla dużych liczebności próby, skośność nie stanowi
żadnego realnego problemu dla testów statystycznych.Jednak skośność jest często związana z dużymi odchyleniami standardowymi. Mogą one skutkować dużymi błędami standardowymi i niską mocą statystyczną. Podobnie, znaczna skośność może zmniejszyć szansę odrzucenia jakiejś hipotezy zerowej w celu wykazania jakiegoś efektu. W tym przypadku, test nieparametryczny może być mądrzejszym wyborem, ponieważ może mieć większą moc.Naruszenia normalności stanowią prawdziwe zagrożenie
dla małych wielkości prób -say- N < 20 lub tak. Przy małych liczebnościach prób, wiele testów nie jest odpornych na naruszenie założenia o normalności. Rozwiązaniem – po raz kolejny – jest użycie testu nieparametrycznego, ponieważ nie wymagają one normalności.
Na koniec, ale nie mniej ważne, nie ma żadnego testu statystycznego do badania, czy skośność populacji = 0. Pośrednim sposobem testowania tego jest test normalności, taki jak
- test normalności Kołmogorowa-Smirnowa i
- test normalności Shapiro-Wilka.
Jednakże, gdy normalność jest naprawdę potrzebna – przy małych rozmiarach próbek – takie testy mają niską moc: mogą nie osiągnąć istotności statystycznej nawet wtedy, gdy odchylenia od normalności są poważne. W ten sposób dają one głównie fałszywe poczucie bezpieczeństwa.
.




