Właściwości Quadrilaterals – Rectangle, Square, Parallelogram, Rhombus, Trapezium
W geometrii euklidesowej, quadrilateral jest czteroboczna 2D figura, której suma kątów wewnętrznych jest 360 °. Słowo czworobok pochodzi od dwóch łacińskich słów „quadri” i „latus” oznaczających odpowiednio cztery i bok. Dlatego identyfikacja właściwości czworokątów jest ważna, gdy próbujemy odróżnić je od innych wielokątów.
Więc, jakie są właściwości czworokątów? Istnieją dwie właściwości czworokątów:
- Czworokąt powinien być zamkniętym kształtem z 4 bokami
- Wszystkie kąty wewnętrzne czworokąta sumują się do 360°
W tym artykule, poznasz 5 typów czworokątów i dowiesz się o właściwościach czworokątów.
To jest to, co przeczytasz w artykule:
- Różne rodzaje czworokątów
- Prostokąt
- Właściwości prostokątów
- Wzory na prostokąty
- Kwadrat
- Właściwości m.in. kwadratu
- Wzory kwadratów
- Równoległobok
- Właściwości równoległoboków
- Wzory równoległoboków
- Romb
- Właściwości rombu
- Wzory rombu
- Trapez/trapez
- Właściwości trapezu
- Wzory trapezu
- Właściwości czworokątów
- Ważne wzory na czworokąty
- Pytania dotyczące czworokątów
Tutaj jest film wyjaśniający właściwości czworokątów:
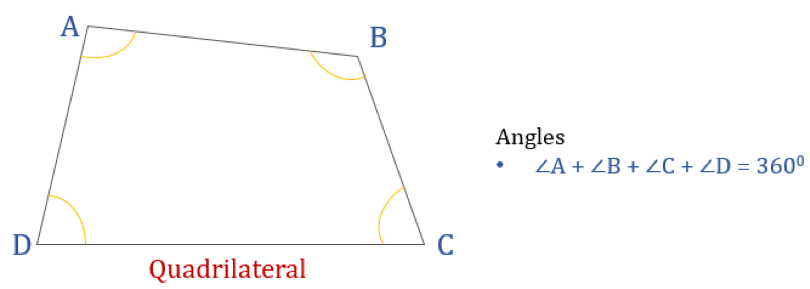
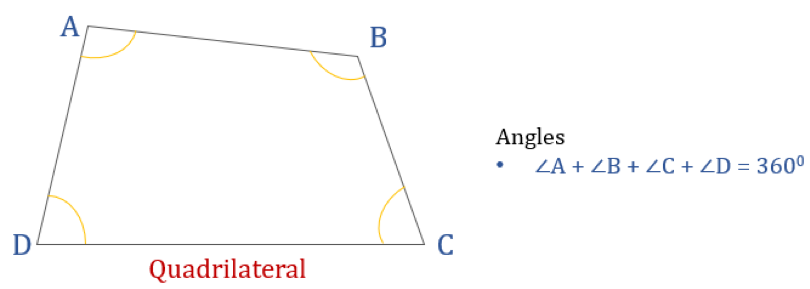
Dany poniżej diagram przedstawia czworokąt ABCD i sumę jego kątów wewnętrznych. Wszystkie kąty wewnętrzne sumują się do 360°.
Tak więc, ∠A + ∠B + ∠C + ∠D = 360°
Różne rodzaje czworokątów
Istnieje 5 rodzajów czworokątów na podstawie ich kształtu. Te 5 czworokątów to:
- Rektangle
- Kwadrat
- Parallelogram
- Rhombus
- Trapez
Przedyskutujmy każdy z tych 5 czworokątów szczegółowo:
Oto pytania, które nauczą Cię jak stosować własności wszystkich 5 czworokątów, które poznasz w tym artykule.
Rectangle
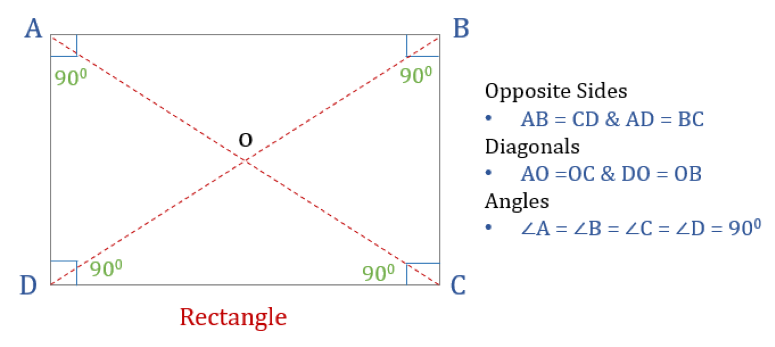
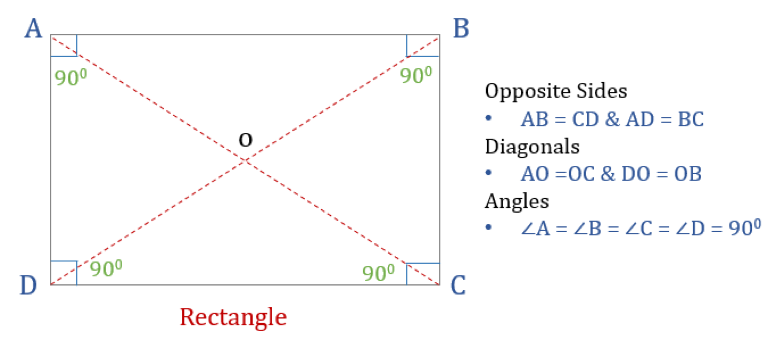
Prostokąt jest czworokątem z czterema kątami prostymi. W związku z tym wszystkie kąty w prostokącie są równe (360°/4 = 90°). Ponadto, przeciwległe boki prostokąta są równoległe i równe, a przekątne przecinają się wzajemnie.
Właściwości prostokątów
Prostokąt ma trzy właściwości:
- Wszystkie kąty prostokąta są równe 90°
- Przeciwległe boki prostokąta są równe i równoległe
- Diagonale prostokąta przecinają się nawzajem
Wzór na prostokąt – Pole i obwód prostokąta
Jeśli długość prostokąta wynosi L, a szerokość B to,
- Powierzchnia prostokąta = Długość × Szerokość lub L × B
- Obwód prostokąta = 2 × (L + B)
Te pytania ćwiczeniowe pomogą Ci utrwalić właściwości prostokątów
Kwadrat
Kwadrat jest czworokątem o czterech równych bokach i kątach. Jest to również regularny czworokąt, ponieważ zarówno jego boki, jak i kąty są równe. Podobnie jak prostokąt, kwadrat ma cztery kąty 90° każdy. Można go również postrzegać jako prostokąt, którego dwa sąsiednie boki są równe.
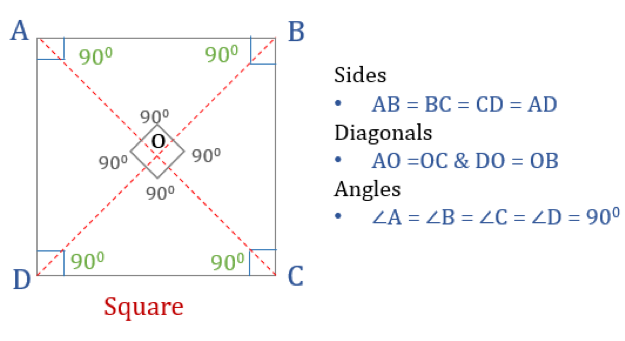
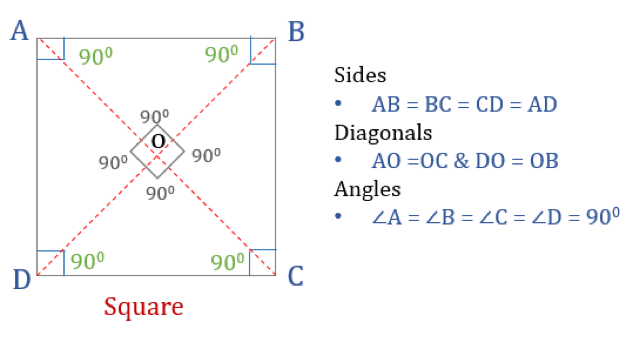
Właściwości kwadratu
Aby czworokąt był kwadratem, musi mieć pewne właściwości. Oto trzy właściwości kwadratów:
- Wszystkie kąty kwadratu są równe 90°
- Wszystkie boki kwadratu są równe i równoległe do siebie
- Diagonale przecinają się prostopadle
Wzór na kwadrat – Pole i obwód kwadratu
Jeśli bok kwadratu jest równy 'a’ to,
- Area of the square = a × a = a²
- Perimeter of the square = 2 × (a + a) = 4a
Te pytania ćwiczeniowe pomogą Ci ugruntować właściwości kwadratów
Zdobycie Q50-51 na GMAT pomoże Ci uzyskać wynik GMAT 700+. Dlaczego nie zaczniesz przygotowywać się do GMAT z naszych bezpłatnych zasobów prep i rozpocząć swoją podróż do uzyskania Q50-51 na GMAT. Ucz się od Carrie Law, która poprawiła się z Q35 do Q50 w 3 tygodnie.
Parallelogram
A równoległobok, jak sama nazwa wskazuje, jest prostym czworokątem, którego przeciwległe boki są równoległe. Zatem ma dwie pary boków równoległych. Ponadto, przeciwległe kąty w równoległoboku są równe, a jego przekątne przecinają się nawzajem.
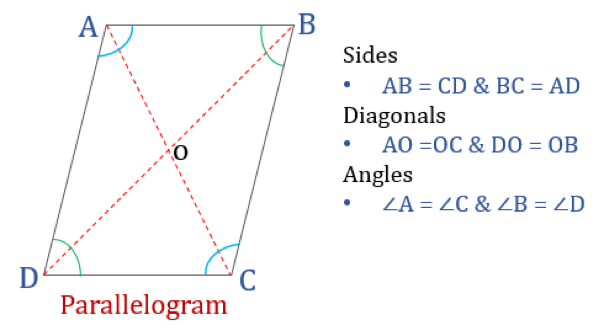
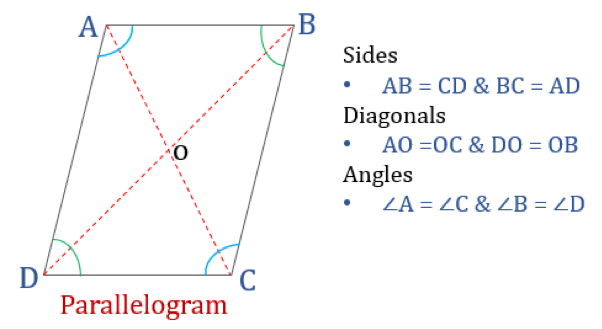
Właściwości równoległoboku
Czworokąt spełniający poniższe właściwości będzie klasyfikowany jako równoległobok. Równoległobok ma cztery własności:
- Kąty przeciwległe są równe
- Boki przeciwległe są równe i równoległe
- Przekątne przekątnych są równe
- Suma dwóch dowolnych kątów przyległych wynosi 180°
Wzory na równoległobok – Pole powierzchni i obwód równoległoboku
Jeśli długość równoległoboku wynosi 'l’, szerokość to 'b’, a wysokość to 'h’, to:
- Obwód równoległoboku= 2 × (l + b)
- Powierzchnia równoległoboku = l × h
Te pytania ćwiczeniowe pomogą Ci utrwalić m.in. własności równoległoboku
Rhombus
Rhombus jest czworokątem, którego wszystkie cztery boki są równej długości, a przeciwległe boki są do siebie równoległe. Jednakże, kąty nie są równe 90°. Romb z kątami prostymi stałby się kwadratem. Inna nazwa rombu to „diament”, ponieważ wygląda on podobnie do koloru karo w kartach do gry.
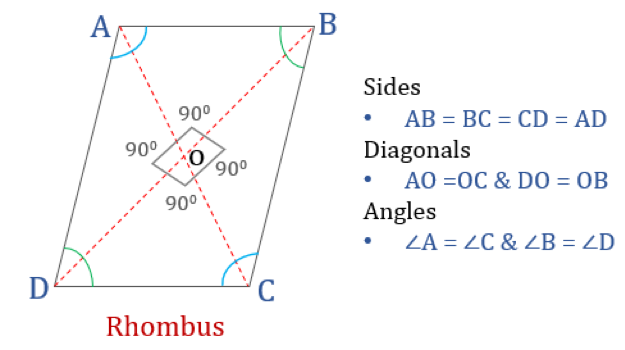
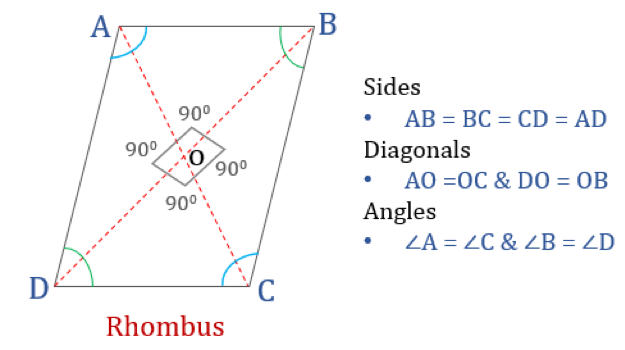
Właściwości rombu
Rzym jest czworokątem, który ma następujące cztery właściwości:
- Kąty przeciwległe są równe
- Wszystkie boki są równe i, przeciwległe boki są do siebie równoległe
- Diagonale przecinają się prostopadle
- Suma dwóch dowolnych kątów przyległych wynosi 180°
Wzory na romb – Pole i obwód rombu
Jeśli bok rombu jest równy a to, obwód rombu = 4a
Jeśli długości dwóch przekątnych rombu to d1 i d2 to pole rombu = ½ × d1 × d2
Te pytania ćwiczeniowe pomogą Ci utrwalić własności rombu
Trapez
Trapez (w USA nazywany trapezem) jest czworokątem, który ma tylko jedną parę boków równoległych. Boki równoległe są nazywane „podstawami”, a pozostałe dwa boki są nazywane „nogami” lub bokami bocznymi.
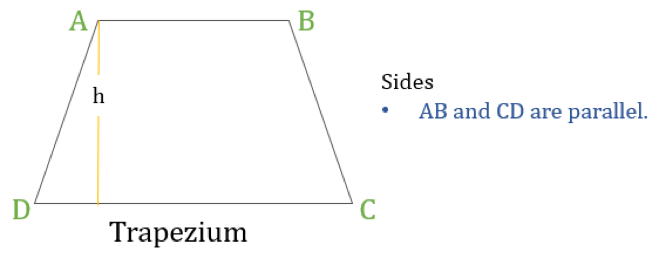
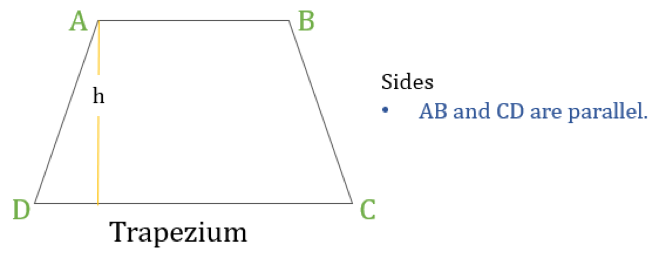
Właściwości trapezu
Trapez jest czworokątem, w którym występuje następująca jedna własność:
- Tylko jedna para przeciwległych boków jest do siebie równoległa
Wzory na trapez – Pole powierzchni i obwód trapezu
Jeśli wysokość trapezu wynosi 'h’ (jak na powyższym rysunku) to:
- Obwód trapezu= Suma długości wszystkich boków = AB + BC + CD + DA
- Powierzchnia trapezu = ½ × (Suma długości boków równoległych) × h = ½ × (AB + CD) × h
Te. pytania ćwiczeniowe pomogą Ci utrwalić własności trapezu
Właściwości czworokątów
Poniższa tabela podsumowuje wszystkie własności czworokątów, które poznaliśmy do tej pory:
| Właściwości czworokątów | Rektangiel | Kwadrat | Paralelogram | Rhombus | Trapez |
| Wszystkie boki są równe | ✖ | ✔ | ✖ | ✔ | ✖ |
| Przeciwległe Boki są równe | ✔ | ✔ | ✔ | ✔ | ✖ |
| Przeciwległe Boki są równoległe | ✔ | ✔ | |||
| Przeciwległe | ✔ | ✔ | ✔ | ✔ | |
| Wszystkie kąty są równe | ✔ | ✔ | ✖ | ✖ | ✖ |
| Kąty przeciwległe są równe | ✔ | ✔ | ✔ | ✔ | ✖ |
| Suma dwóch kątów przyległych wynosi 180 | ✔ | ✔ | ✔ | ✖ | |
| Bisect each other | ✔ | ✔ | ✔ | ✔ | ✖ |
| Bisect perpendicularly | |||||
| Bisect perpendicularly | ✖ | ✔ | ✖ | ✔ | ✖ |
Poniższy obrazek również podsumowuje własności czworokątów:
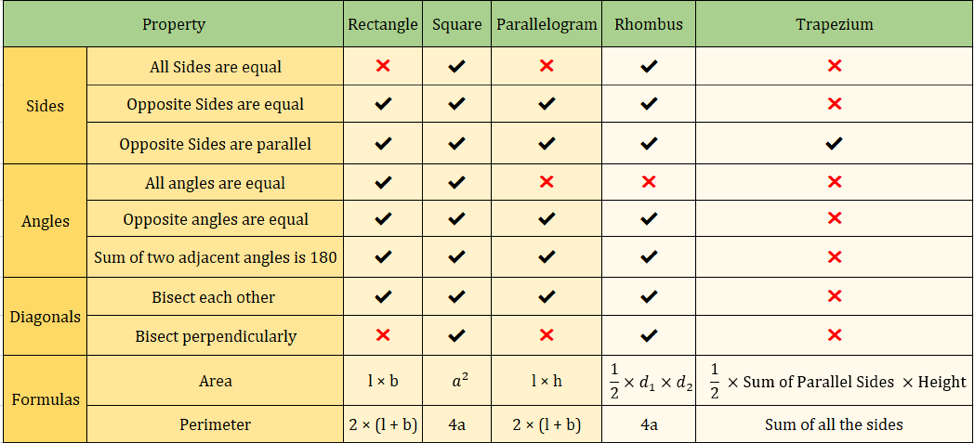
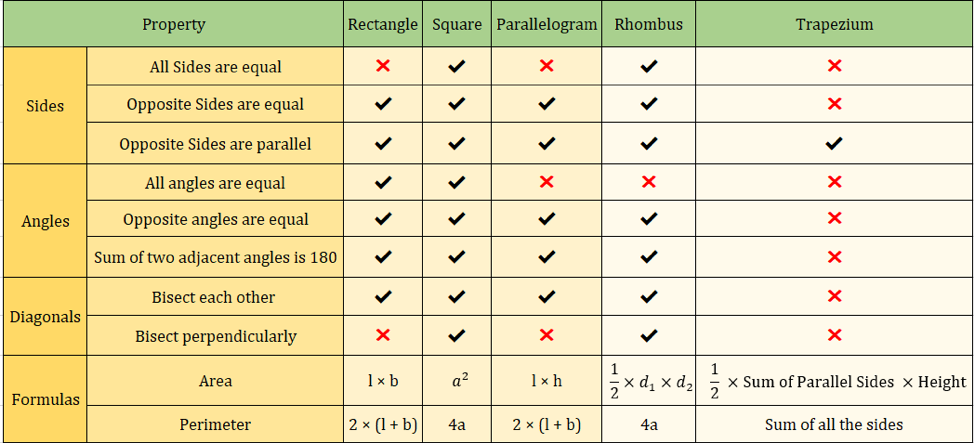
Ważne wzory na czworokąty
Poniższa tabela podsumowuje wzory na pole i obwód różnych typów czworokątów:
| Wzory na czworokąty | Rektangiel | Kwadrat | Paralelogram | Rhombus | Trapez |
| Area | l × b | a² | l × h | ½ × d1 × d2 | ½ × (suma boków równoległych) × wysokość |
| Perymetr | 2 × (l + b) | 4a | 2 × (l + b) | 4a | Suma wszystkich boków |
Dalsza lektura:
- Właściwości okręgu | Wzory na okrąg – Pole i obwód
- Właściwości liczb – Parzyste & Nieparzyste | Liczby pierwsze | HCF & LCM
- Właściwości trójkątów – Definicja | Rodzaje | Klasyfikacja
- Właściwości trójkątów – Definicja | Rodzaje. Klasyfikacja
- Linie i kąty – własności i ich zastosowanie
Pytania dotyczące czworokątów
Przećwiczmy zastosowanie własności czworokątów na poniższych przykładowych pytaniach:
Pytanie 1
Adam chce zbudować ogrodzenie wokół swojego prostokątnego ogrodu o długości 10 metrów i szerokości 15 metrów. Ile metrów płotu powinien kupić, aby ogrodzić cały ogród?
- 20 metrów
- 25 metrów
- 30 metrów
- 40 metrów
- 50 metrów
Rozwiązanie
Krok 1: Dane
- Adam ma prostokątny ogród.
- Ma on długość 10 metrów i szerokość 15 metrów.
- Chce zbudować wokół niego płot.
Krok 2: Znaleźć
- Długość potrzebną do zbudowania płotu wokół całego ogrodu.
Krok 3: Podejście i Wypracowanie
Płot można zbudować tylko wokół zewnętrznych boków ogrodu.
- Więc, całkowita długość potrzebnego płotu= Suma długości wszystkich boków ogrodu.
- Ponieważ ogród jest prostokątny, suma długości wszystkich boków to nic innego jak obwód ogrodu.
- Obwód = 2 × (10 + 15) = 50 metrów
Wynika z tego, że wymagana długość ogrodzenia wynosi 50 metrów.
Więc opcja E jest poprawną odpowiedzią.
Pytanie: 2
Steve chce pomalować jedną ścianę swojego pokoju w kształcie prostokąta. Koszt pomalowania tej ściany wynosi 1,5 dolara za metr kwadratowy. Jeśli ściana ma 25 metrów długości i 18 metrów szerokości, to jaki jest całkowity koszt pomalowania tej ściany?
- $ 300
- $ 350
- $ 450
- $ 600
- $ 675
Rozwiązanie
Krok 1: Dane
- Steve chce pomalować jedną ścianę w swoim pokoju.
- Ściana ma 25 metrów długości i 18 metrów szerokości.
- Koszt pomalowania ściany wynosi 1,5 dolara za metr kwadratowy.
Krok 2: Aby znaleźć
- Całkowity koszt pomalowania ściany.
Krok 3: Podejście i wypracowanie
- Ściana jest pomalowana na całej swojej powierzchni.
- Jeśli więc znajdziemy całkowitą powierzchnię ściany w metrach kwadratowych i pomnożymy ją przez koszt pomalowania 1 metra kwadratowego ściany, otrzymamy koszt całkowity.
- Powierzchnia ściany = długość × szerokość = 25 metrów × 18 metrów = 450 metrów kwadratowych
- Całkowity koszt pomalowania ściany = 450 × $1.5 = $675
Więc poprawną odpowiedzią jest opcja E.
Mamy nadzieję, że do tej pory nauczyłeś się różnych typów czworokątów, ich właściwości i wzorów oraz jak stosować te pojęcia do rozwiązywania pytań dotyczących czworokątów. Zastosowanie czworokątów jest ważne dla rozwiązywania pytań z geometrii na GMAT. Jeśli planujesz przystąpić do egzaminu GMAT, możemy Ci pomóc dzięki wysokiej jakości materiałom do nauki, do których możesz uzyskać dostęp za darmo, rejestrując się tutaj.
Tutaj jest jeszcze kilka artykułów na temat Math:
- Improve accuracy in Math questions on Polygons
- Geometry Questions – Most Common Mistakes | GMAT Quant Prep
Jeśli planujesz wziąć GMAT, możemy dać ci dostęp do wysokiej jakości treści online, aby się przygotować. Jesteśmy najczęściej recenzowaną firmą przygotowującą do GMAT na gmatclub z ponad 1950 recenzjami.
Dlaczego nie weźmiesz darmowej wersji próbnej i nie ocenisz sam?
Pisz do nas na [email protected] w przypadku jakichkolwiek pytań.




