Área de Superfície de um Cilindro – Explicação & Exemplos
Antes de saltarmos para o tópico da área de superfície de um cilindro, vamos rever um cilindro. Em geometria, um cilindro é uma figura tridimensional com duas bases circulares paralelas uma à outra e uma superfície curva.
Como encontrar a área de superfície de um cilindro?
A área de superfície de um cilindro é a soma de duas faces circulares paralelas e congruentes e a área da superfície curva.
Este artigo irá discutir como encontrar a área total de superfície e a área de superfície lateral de um cilindro.
Para calcular a área de superfície de um cilindro, você precisa encontrar a Área de Base (B) e a Área de Superfície Curva (CSA). Portanto, a área de superfície ou a superfície total de um cilindro é igual à soma da área de base vezes dois e a área da superfície curva.
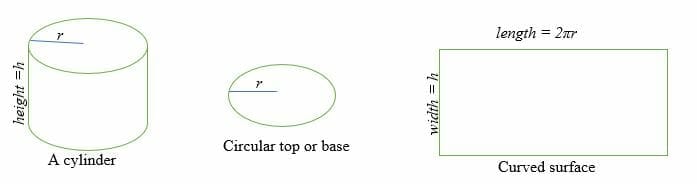
A superfície curva de um cilindro é igual a um retângulo cujo comprimento é 2πr e cuja largura é h.
Onde r = raio da face circular e h = altura do cilindro.
A área da superfície curva = Área de um rectângulo =l x w = πdh
A área da base, B =A área de um círculo = πr2
A área de uma fórmula de cilindro
A fórmula da área total da superfície de um cilindro é dada como:
Área total da superfície de um cilindro = 2πr2 + 2πrh
TSA = 2πr2 + 2πrh
Onde 2πr2 é a área da face circular superior e inferior, e 2πrh é a área da superfície curvada.
Tomando 2πr como fator comum do RHS, obtemos;
TSA = 2πr (h + r) ……………………………………. (Área da superfície de uma fórmula do cilindro)
Solucionemos exemplos de problemas envolvendo a área da superfície de um cilindro.
>
Exemplo 1
Ponhamos a área total de superfície de um cilindro cujo raio é 5 cm e altura é 7 cm.
Solução
Pela fórmula,
TSA = 2πr (h + r)
= 2 x 3.14 x 5(7 + 5)
= 31,4 x 12
= 376,8 cm2
Exemplo 2
Pelo raio de um cilindro cuja superfície total é de 2136,56 pés quadrados, e a altura é de 3 pés.
Solução
Dado:
TSA = 2136.56 pés quadrados
Altura, h = 3 pés
But, TSA = 2πr (h + r)
2136,56 =2 x 3,14 x r (3 + r)
2136,56 = 6.28r (3 + r)
Por propriedade distributiva de multiplicação no RHS, temos,
2136,56 = 18,84r + 6,28r2
Dividir cada termo por 6,28
340.22 = 3r + r2
r2 + 3r – 340,22 = 0 ……… (uma equação quadrática)
Resolvendo a equação usando a fórmula quadrática, obtemos,
r = 17
Assim, o raio do cilindro é de 17 pés.
Exemplo 3
O custo de pintar um recipiente cilíndrico é de 0,04 dólares por cm2. Encontre o custo de pintar 20 recipientes de raio, 50 cm, e altura, 80 cm.
Solução
Calcular a área total de superfície de 20 recipientes.
TSA = 2πr (h + r)
= 2 x 3.14 x 50 (80 + 50)
= 314 x 130
= 40820 cm2
A área total de superfície de 20 recipientes = 40.820 cm2 x 20
=816.400 cm2
O custo de pintura = 816.400 cm2 x $0.04 por cm2
= $32.656,
Hence, o custo de pintar 20 recipientes é de $32.656,
Exemplo 4
Perguntar a altura de um cilindro se sua área total de superfície é 2552 in2 e o raio é 14 in.
Solução
Dado:
TSA = 2552 in2
Radius, r = 14 in.
But, TSA = 2πr (h + r)
2552 = 2 x 3.14 x 14 (14 + h)
2552 = 87,92(14 + h)
Dividir ambos os lados por 87,92 para obter,
29.026 = 14 + h
Subtrair por 14 em ambos os lados.
h = 15
Hence, a altura do cilindro é 15 in.
Área de superfície lateral de um cilindro
Como dito anteriormente, a área da superfície curva de um cilindro é o que é chamado de área de superfície lateral. Em palavras simples, a área da superfície lateral de um cilindro é a área da superfície de um cilindro, excluindo a área da base e do fundo (superfície circular).
A fórmula dá a área da superfície lateral de um cilindro;
LSA = 2πrh
Exemplo 5
Ponha a área da superfície posterior de um cilindro cujo diâmetro é 56 cm e altura é 20 cm.
Solução
Dado:
Diâmetro = 56 cm, daí raio, r =56/2 = 28 cm
Altura, h = 20 cm
Por, a fórmula,
LSA = 2πrh
>
= 2 x 3.14 x 28 x 20
= 3516,8 cm2,
Assim, a superfície lateral do cilindro é de 3516,8 cm2,
Exemplo 6
A superfície lateral de um cilindro é de 144 pés2. Se o raio do cilindro for 7 pés, encontre a altura do cilindro.
Solução
Dado;
LSA = 144 pés2
Radius, r = 7 pés




