Entropia – O Pilar da Termodinâmica e Teoria da Informação
Entropia é um termo vago mas poderoso que forma a espinha dorsal de muitas ideias chave em Termodinâmica e Teoria da Informação. Foi identificada pela primeira vez por cientistas físicos no século 19 e atuou como um princípio orientador para muitas das tecnologias revolucionárias da Revolução Industrial. Contudo, o termo também ajudou a desencadear a Era da Informação quando apareceu no trabalho pioneiro do matemático Claude Shannon A Mathematical Theory of Communication. Então como pode um termo ser responsável por dois avanços, com cerca de um século de diferença, em campos relacionados mas díspares?
Primeiro, vamos começar com como a entropia é interpretada nas ciências físicas. A Primeira Lei da Termodinâmica estipula que em qualquer sistema fechado, a energia não pode ser criada nem destruída. A Segunda Lei, também conhecida como Lei da Entropia, estipula que num sistema aberto, a energia flui sempre de uma concentração mais alta para uma concentração mais baixa, a fim de alcançar o equilíbrio termodinâmico. O que isto significa na prática? Significa que sua caneca de café acaba esfriando e o gelo da bebida derrete com o tempo, ou que uma ferramenta colocada no fogo irá aquecer à medida que a energia da chama se transfere para as moléculas de ferro, mas esfriar assim que for removida à medida que a energia se distribui pelo novo ambiente ao redor.

O próprio termo entropia refere-se ao estado de desordem em um determinado sistema. A energia na forma concentrada e utilizável é considerada ordenada, enquanto a energia na forma distribuída e indisponível é considerada desordenada.
A entropia move-se apenas em uma direção – em direção ao equilíbrio – a menos que seja agida por uma força fora do sistema, e mesmo assim, forças externas como os sistemas biológicos só conseguem reverter temporariamente o processo de entropia e, em última instância, se desprendem (via morte). Qualquer planta ou animal é um sistema energético complexo que sobrevive compensando o processo entropico e recolhendo a energia disponível, ordenando a energia do meio ambiente e depois emitindo resíduos despojados de nutrientes. Mas a produção de energia no sistema vivo acaba por degradar a sua estrutura física, fazendo com que o organismo se decomponha e morra (esperemos que tenha completado o seu objectivo final de reprodução). O corpo de energia, não mais vivo, irá decompor-se e dissipar-se no ambiente circundante – e no equilíbrio termodinâmico.
Teóricamente, a entropia só descansará a sua marcha constante uma vez que tenha trazido a morte por calor do universo – um estado final final onde não há energia livre. Tudo na Terra e no espaço irá eventualmente expandir-se, explodir, morrer e distribuir energia livre uniformemente através daquele que é realmente o maior sistema fechado de todos: o Universo. Desta forma, a entropia é uma lei universal semelhante à gravidade, pois opera tanto na menor como na maior escala da biofísica.
Economias são organismos, não máquinas de lavar roupa
Entropia também se aplica à economia. O processo de entropia dentro de um organismo, ao adquirir energia disponível do ambiente circundante e ao transformá-la em energia desordenada, também se aplica a grupos de organismos. As sociedades tomam fontes de energia de baixa entropia em duas formas: stocks e fluxos. Os estoques incluem minerais terrestres raros, combustíveis fósseis e outros depósitos terrestres criados por processos terrestres complexos e de longo prazo ao longo de milênios. Os fluxos têm origem no que são considerados fontes renováveis, como o vento, a água e a energia solar, que também incluem a biomassa (como uma extensão indireta da energia solar). Dada a natureza de cada fonte, os estoques são limitados em quantidade, enquanto que os fluxos são limitados tanto em taxa como em quantidade. As civilizações, tal como os organismos, têm metabolismos. Elas processam energia.

A Revolução Industrial deslocou pela primeira vez a entrada de energia primária da economia dos fluxos para os estoques terrestres. Arados e velas de vento, duas formas de trabalho dependentes de fluxos, foram substituídos por agricultura mecanizada e embarcações movidas a vapor, que dependem de combustíveis fósseis. Aproveitamos a energia solar dormente fossilizada durante milhões de anos para libertar a civilização das restrições dos fluxos biológicos da terra e criar um crescimento vertiginoso da população e do PIB.
Apesar das inegáveis vantagens econômicas e materiais dessa mudança, ela teve o efeito colateral de apressar o processo de entropia e aumentar a desordem no sistema climático. Embora a quantidade total de energia permaneça inalterada através do processo econômico (com exceção da energia solar), a mineração de minerais e o consumo de combustíveis fósseis necessários para o processo de produção caracteriza uma mudança qualitativa que move a energia da ordem para a desordem. Desta forma, a entropia forma a base da escassez porque os seres humanos não podem mover a energia de outro modo, de um estado de desordem para a ordem; sem entropia, seria fisicamente possível transformar o CO2 atmosférico num pedaço de carvão, tal como seria possível capturar e reconfigurar as partículas de borracha perdidas à medida que um pneu se degrada no pavimento.

No final do dia, a nossa economia utiliza coisas e energia. Ainda que o dinheiro, nossa representação de valor, circule através da economia indefinidamente, os bens físicos que ela representa estão sujeitos à lei da entropia. O sistema econômico atual é como um organismo que cresce indefinidamente. Nosso coração bombeia nosso sangue e nos mantém vivos, mas a força desgasta nossas células ao longo do tempo. Nós envelhecemos e nos degradamos.
Então como a entropia se aplica à ciência dos dados?
Agora demos uma olhada em como a entropia se refere à energia, vejamos como ela se aplica à comunicação e à Teoria da Informação. Penso que este excerto da biografia de Jimmy Soni e Rob Goodman de Claude Shannon, A Mind at Play, é uma grande história anedótica das origens da entropia:
Shannon abordou o grande homem com a sua ideia de incerteza de informação-resolvida – que viria a estar no centro do seu trabalho – e com uma pergunta sem pretensões. Como ele deveria chamar essa coisa? Von Neumann respondeu imediatamente: “Diga que a informação reduz a ‘entropia'”. Para um é uma boa e sólida palavra física. E o mais importante”, prosseguiu ele, “ninguém sabe o que é realmente entropia, então em um debate você sempre terá a vantagem.”

Antes de assumir a definição de entropia de Shannon, pode ajudar a quebrar a sua definição de informação. A idéia básica da teoria de Shannon é que o valor informativo de uma mensagem comunicada depende do grau em que o conteúdo da mensagem é surpreendente. Um grande exemplo disso na prática é o uso da frequência das letras na linguagem. Probabilisticamente, se a instância de uma letra é um evento, então o resultado mais provável de cada evento dado segue esta distribuição de probabilidade:
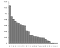
> Quanto mais letras houver, menos incerteza há na mensagem. Mas isso também depende da raridade da letra. Por exemplo, qual das seguintes mensagens contém mais de um soco informativo, 1 ou 2?
_AT
Opção “1” inclui duas letras com probabilidades relativamente altas, onde se pode soletrar todo o tipo de palavras através do preenchimento da letra em falta: “Morcego”, “Gato”, “Chapéu”, “Gordura”, “Sáb”, etc. A Opção 2 inclui a letra relativamente esquiva “H”, que tem algumas opções de palavras restantes como “Hat” ou “Hit”, mas não tantas como a Opção 1. Portanto, a Opção 2 comunica mais informações porque reduz a incerteza a um grau maior.
Então se a informação é resolvida a incerteza, a entropia deve ser a incerteza que precisa ser resolvida. A raridade de um evento, ou sua “surpresa”, determina seu conteúdo de informação (se você já jogou Scrabble, você saberia como as opções seriam limitadas se desenhássemos a letra “Q”). Cada vez que comunicamos uma informação, a entropia geral, desordem, incerteza, ou o que quer que lhe queira chamar, diminui numa quantidade ou taxa proporcional. Então, qual é essa quantidade proporcional?
Shannon calculou que a medida da entropia de informação associada a cada valor de dado possível é o logaritmo negativo da função massa de probabilidade para o valor:
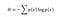
Entropia mede a quantidade esperada de informação transmitida através da identificação do resultado de um evento aleatório, onde os possíveis resultados são uma função de probabilidade. Isto implica que o lançamento de um dado tem uma entropia maior do que o lançamento de uma moeda porque cada resultado de um lançamento de dado (⅙) tem uma probabilidade menor do que o lançamento sobre a cabeça ou cauda (½). Olhando a relação graficamente ajuda:

Ao comunicar um resultado de cabeças, sabemos que não ocorreram caudas.
Na aprendizagem da máquina, a interpretação matemática da entropia é usada para calcular uma métrica de ganho de informação para muitos algoritmos. Árvores de decisão, por exemplo, selecionam um dos muitos atributos diferentes, também conhecidos como características ou variáveis independentes, para dividir repetidamente amostras em subconjuntos. Em cada divisão, o algoritmo seleciona um atributo para dividir a amostra e continua a fazê-lo até que todos os subconjuntos sejam puros, ou seja, cada amostra individual de um subconjunto compartilha a mesma classificação ou valor-alvo.
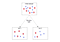
Para medir a pureza de um subconjunto de amostra, o algoritmo precisa de uma medida quantitativa para escolher objetivamente qual característica a ser dividida em cada nó dado. É aqui que entra a entropia. Em cada etapa, o algoritmo calcula qual atributo irá mostrar o maior ganho de informação, e então decide sobre a divisão. Ele também calcula a diminuição esperada da incerteza antes e depois da divisão; se ela diminuir, a divisão é mantida e o algoritmo prossegue para a próxima etapa. Se não tiver diminuído, atingiu a pureza e descansa. Desta forma, ele é responsável tanto pela seleção da característica a ser dividida quanto pela interrupção do processo.
Existe uma ligação entre termodinâmica e Teoria da Informação?
Entropia flui inexoravelmente através de uma árvore de decisão assim como flui inexoravelmente através de uma xícara de café para o ar. Em energia, ela marcha para o equilíbrio termodinâmico; em Teoria da Informação, ela marcha para a pureza.
No seu núcleo, a interpretação energética da entropia e a interpretação da teoria da informação da entropia convergem no mesmo ponto – as leis fundamentais da física. A comunicação requer energia, e o uso de energia requer comunicação. De acordo com Shannon, o valor da entropia de um pedaço de informação fornece um limite absoluto no menor comprimento médio possível de uma mensagem, ou quanto ela pode ser comprimida, sem perder informação à medida que é transmitida. Semicondutores, lanternas, e bater em uma panela em Código Morse requer energia humana, e nossas comunicações sempre se esforçarão pelo meio mais eficiente de transmissão.
Em energia, tentamos minimizar a entropia limitando o quanto consumimos e o quão eficientemente a consumimos. Nosso objetivo é encontrar fontes ordenadas de energia e resistir à influência da entropia em nossos corpos. Nas comunicações, nós minimizamos a entropia encontrando informações e reduzindo a incerteza. De certa forma, ao reduzir a desordem através da comunicação, podemos parar o processo entropico de energia; um caçador-colector pode usar a linguagem para comunicar com outro para avisar sobre ser comido por um leão, ambos reduzindo a incerteza de 1. onde está o leão (entropia de informação) e 2. o processo de ser comido por um leão (entropia de energia). Este acto de comunicação reduz o espaço de probabilidade de todos os eventos possíveis e permite-nos agir de forma mais eficiente e eficaz. Compreender a natureza de como esta poderosa lei opera nos reinos digital e físico é a chave para compreender as conexões entre termodinâmica e a era da informação.




