Método da Divisão Sintética
Devo dizer que a divisão sintética é a forma mais “divertida” de dividir os polinómios. Tem menos passos para chegar à resposta em comparação com o método de divisão polinomial longa. Nesta lição, vou passar por cinco (5) exemplos que espero que o familiarizem com os procedimentos básicos para dividir com sucesso os polinómios usando a divisão sintética.
>
Coisas a Recordar:
- Certifique-se de que o dividendo está na forma padrão. Isso significa que os poderes estão em ordem decrescente.
- O divisor deve estar na forma x – \ esquerda( c \ direita).
Exemplos de como dividir polinómios usando a divisão sintética
Exemplo 1: Divida o polinômio abaixo.
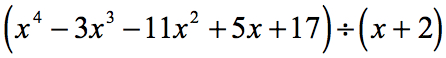
Deixe-nos reexaminar o problema dado e fazer os ajustes necessários, se necessário.
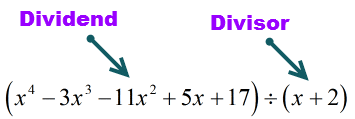
O dividendo (material a dividir) está na forma padrão porque os expoentes estão em ordem decrescente. Isso é bom!
O divisor precisa ser reescrito como
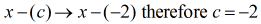
Neste ponto, posso agora configurar a divisão sintética extraindo os coeficientes do dividendo e depois alinhando-os no topo.
Diretamente para o lado esquerdo, coloque o valor de c = – 2 dentro da “caixa”.
Finalmente, construa uma linha horizontal logo abaixo dos coeficientes do dividendo.
Passos:
1. Deixe cair o primeiro coeficiente abaixo da linha horizontal.
2. Multiplique o número que você deixar cair pelo número na “caixa”. Qualquer que seja seu produto, coloque-o acima da linha horizontal logo abaixo do segundo coeficiente.
3. Adicione a coluna de números, depois coloque a soma diretamente abaixo da linha horizontal.
4. Repita o processo até ficar sem colunas para adicionar.
Veja a solução animada abaixo:
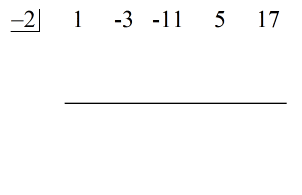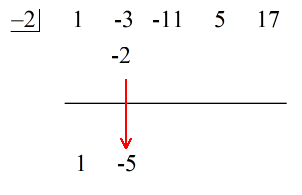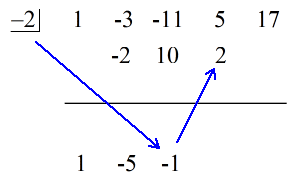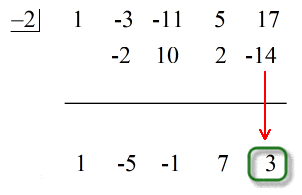
O último número abaixo da linha horizontal é sempre o restante! O restante deste problema é 3.
>
Então como apresentamos nossa resposta final?
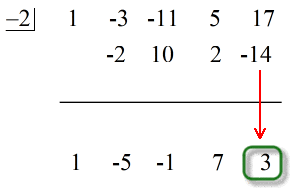
- Mostrar sua resposta final no formulário
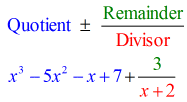
>
Notem que os números abaixo da linha horizontal, exceto o último (restante), são os coeficientes do Quociente.
Mais ainda, os expoentes das variáveis do quociente são todos reduzidos em 1,
Exemplo 2: Dividir o polinômio.
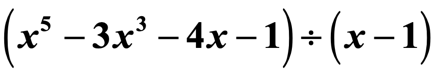
Esta não é uma pergunta com rasteira. Note que o quociente não tem todos os expoentes da variável x.
Vejo que nos faltam {x^4} e {x^2}. Para incluir todos os coeficientes da variável x em potência decrescente, devemos reescrever o problema original desta forma. Anexe zeros nos x que faltam. Também expresse o divisor como x – (c) que revela claramente o valor de c, ou seja, c = + 1.
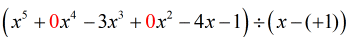
A partir deste ponto, posso agora configurar os números para continuar com o processo.
Passos:
1. Deixe cair o primeiro coeficiente abaixo da linha horizontal.
2. Multiplique o número que você deixar cair pelo número na “caixa”. Qualquer que seja seu produto, coloque-o acima da linha horizontal logo abaixo do segundo coeficiente.
3. Adicione a coluna de números, depois coloque a soma diretamente abaixo da linha horizontal.
4. Repita o processo até ficar sem colunas para adicionar.
Veja a solução animada abaixo:
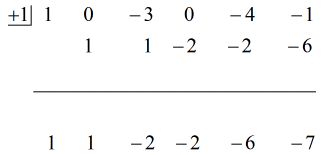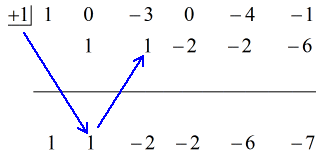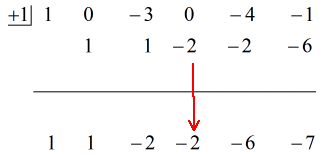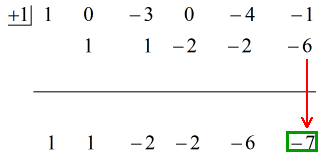
Ponha a resposta final no formulário
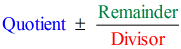
temos
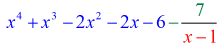
Exemplo 3: Divida o polinómio abaixo.
>
esquerda( { – 2{x^4} + x} {direita) {div {x – 3} {direita)
>
Esta é cada vez mais interessante! O quociente parece definitivamente horrível porque está faltando muito. Não só lhe faltam alguns x’s que são {x^3} e {x^2} mas a constante também desapareceu.
Para corrigir isto, vou reescrever o problema original de tal forma que todos os x’s sejam contabilizados. Mas mais importante, não se esqueça de incluir a constante que falta, que é zero.
O problema “novo e melhorado” deve ficar assim:
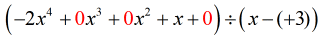
Daqui, prossiga com os passos como de costume.
Passos:
1. Deixe cair o primeiro coeficiente abaixo da linha horizontal.
2. Multiplique o número que você deixar cair pelo número na “caixa”. Qualquer que seja seu produto, coloque-o acima da linha horizontal logo abaixo do segundo coeficiente.
3. Adicione a coluna de números, depois coloque a soma diretamente abaixo da linha horizontal.
4. Repita o processo até ficar sem colunas para adicionar.
Ver solução animada abaixo:
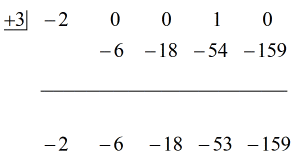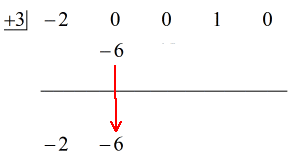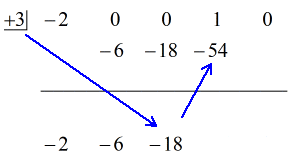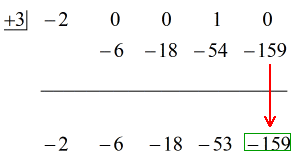
Okay então, a resposta final para isto é
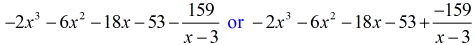
Pode escrever a resposta final de duas maneiras. A primeira é usando o símbolo de menos ou subtração para indicar que o restante é negativo. A segunda é usando o símbolo + mas anexando um símbolo negativo ao numerador. Eles significam a mesma coisa!
Exemplo 4: Divida o polinômio abaixo.
\esquerda( { – {x^5} + 1} \direita) \div \esquerda( {x + 1} \direita)
Não se desencoraje com este problema. Isto é realmente muito fácil, especialmente agora que você já passou por alguns exemplos. Lembre-se sempre de “preencher as partes que faltam”, certo?
Observe o dividendo e você deve concordar que as partes que faltam são {x^4}, {x^3}, {x^2}, e x.
Reescrevendo o problema original que está pronto para a divisão sintética, obtemos…
Populamos os x’s em falta com zeros e resolvemos explicitamente para c = -1.
Passos:
1. Deixe cair o primeiro coeficiente abaixo da linha horizontal.
2. Multiplique o número que você deixar cair pelo número na “caixa”. Qualquer que seja seu produto, coloque-o acima da linha horizontal logo abaixo do segundo coeficiente.
3. Adicione a coluna de números, depois coloque a soma diretamente abaixo da linha horizontal.
4. Repita o processo até ficar sem colunas para adicionar.
Veja a solução animada abaixo:
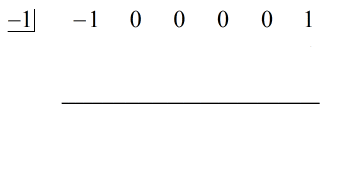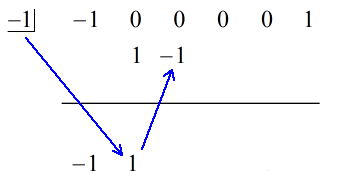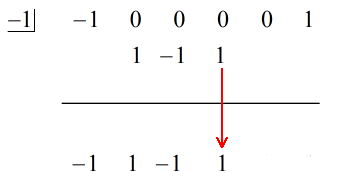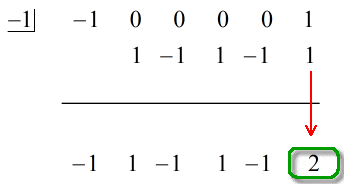
O último número abaixo da linha horizontal será sempre o restante. Não se esqueça disso. Neste caso, o restante é igual a 2,
Nossa resposta final é
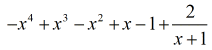
Exemplo 5: Dividir o polinômio por um binômio.
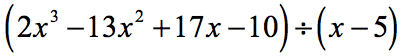
Neste exemplo, teremos um restante de zero. Quando isso acontece o divisor torna-se um fator do dividendo. Em outras palavras, o divisor divide uniformemente o dividendo.
Ao examinar o problema, vejo que não há componentes ausentes. Todos os poderes de x são contabilizados, e temos uma constante. Isso é óptimo! Este problema está de facto pronto para a divisão sintética.
Passos:
1. Deixe cair o primeiro coeficiente abaixo da linha horizontal.
2. Multiplique o número que você deixar cair pelo número na “caixa”. Qualquer que seja seu produto, coloque-o acima da linha horizontal logo abaixo do segundo coeficiente.
3. Adicione a coluna de números, depois coloque a soma diretamente abaixo da linha horizontal.
4. Repita o processo até ficar sem colunas para adicionar.
Veja a solução animada abaixo:
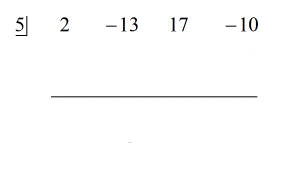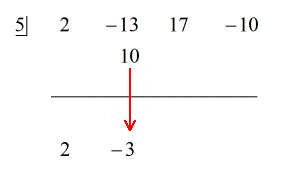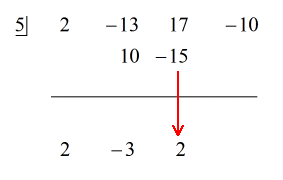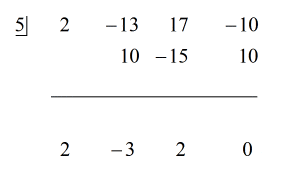
Porque o restante é igual a zero, isto significa que o divisor x – 5 é um fator do dividendo
antes
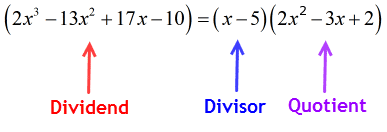
Prática com Fichas de Trabalho
Você também pode estar interessado em:
>
Adicionar e Subtrair Polinómios
Dividir Polinómios pelo Método da Divisão Longa
Multiplicar Binômios pelo Método FOIL
Multiplicar Polinómios




