Propriedades dos Quadriláteros – Retângulo, Quadrado, Paralelogramo, Ródulo, Trapézio
Em geometria Euclidiana, um quadrilátero é uma figura 2D de quatro lados cuja soma dos ângulos internos é de 360°. A palavra quadrilátero é derivada de duas palavras latinas ‘quadri’ e ‘latus’ que significam quatro e lado respectivamente. Portanto, identificar as propriedades dos quadriláteros é importante quando se tenta distingui-los de outros polígonos.
Então, quais são as propriedades dos quadriláteros? Existem duas propriedades dos quadriláteros:
- Um quadrilátero deve ter forma fechada com 4 lados
- Todos os ângulos internos de um quadrilátero somam até 360°
Neste artigo, você terá uma idéia sobre os 5 tipos de quadriláteros e conhecerá as propriedades dos quadriláteros.
Isto é o que você vai ler no artigo:
- Diferentes tipos de quadriláteros
- Rectângulo
- Propriedades de rectângulos
- Fórmulas de rectângulos
- Quadrado
- Propriedades de um quadrado
- Fórmulas de quadrados
- Paralelogramo
- Propriedades de paralelogramo
- Fórmulas de paralelogramo
- Rhombus
- Propriedades de um losango
- Fórmulas de um losango
- Trapézio/Trapézio
- Propriedades de um trapézio
- Fórmulas de um trapézio
- Propriedades de quadriláteros
- Fórmulas importantes de quadriláteros
- Quadrilaterais
Aqui está um vídeo que explica as propriedades dos quadriláteros:
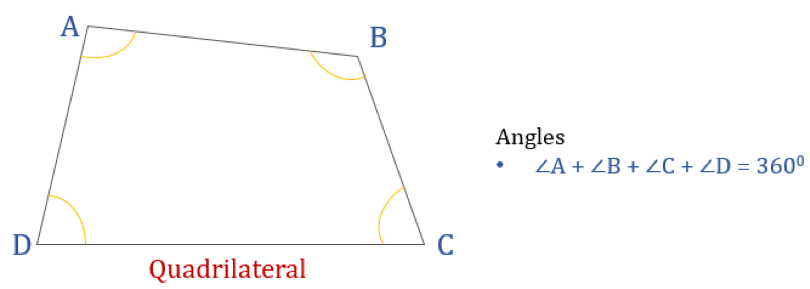
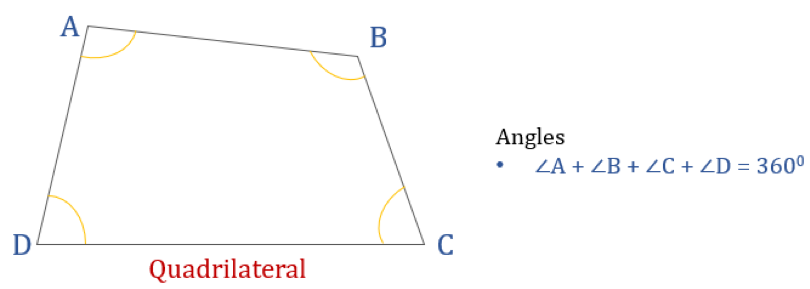
O diagrama abaixo mostra um quadrilátero ABCD e a soma dos seus ângulos internos. Todos os ângulos internos somam até 360°.
Assim, ∠A + ∠B + ∠C + ∠D = 360°
Diferentes tipos de quadriláteros
Existem 5 tipos de quadriláteros com base na sua forma. Estes 5 quadriláteros são:
- Rectângulo
- Quadrado
- Parallelograma
- Rhombus
- Trapézio
Vamos discutir cada um destes 5 quadriláteros em detalhe:
Aqui estão as perguntas que lhe ensinarão como aplicar as propriedades de todos os 5 quadriláteros que vai aprender neste artigo.
Rectângulo
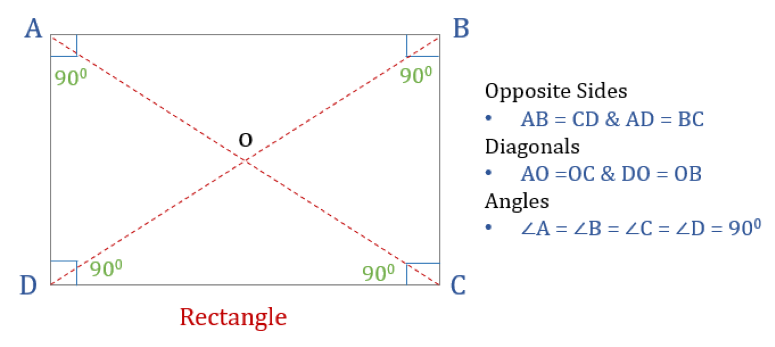
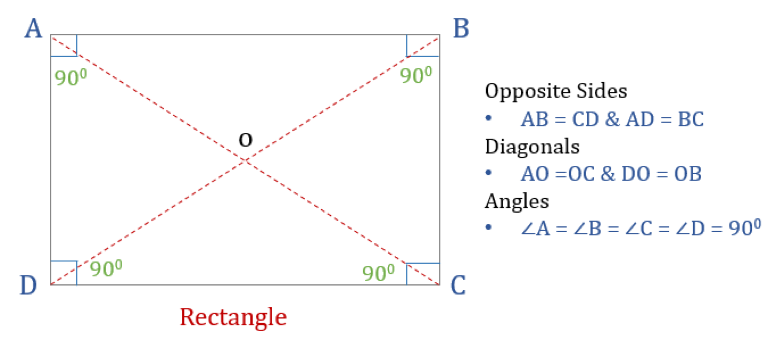
Um rectângulo é um quadrilátero com quatro ângulos rectos. Assim, todos os ângulos em um retângulo são iguais (360°/4 = 90°). Além disso, os lados opostos de um retângulo são paralelos e iguais, e as diagonais se bissetam umas às outras.
Propriedades de rectângulos
Um rectângulo tem três propriedades:
- Todos os ângulos de um rectângulo são 90°
- Os lados opposite de um rectângulo são iguais e Paralelos
- Diagonais de um rectângulo bissectam-se uns aos outros
Fórmula rectangular – Área e perímetro de um rectângulo
Se o comprimento do rectângulo é L e a largura é B então,
- Área de um rectângulo = Comprimento × Largura ou L × B
- Perímetro do rectângulo = 2 × (L + B)
Estas questões práticas irão ajudá-lo a solidificar as propriedades dos rectângulos
Quadrado
Quadrado é um quadrilátero com quatro lados e ângulos iguais. É também um quadrilátero regular, pois tanto os seus lados como os seus ângulos são iguais. Tal como um rectângulo, um quadrado tem quatro ângulos de 90° cada. Também pode ser visto como um retângulo cujos dois lados adjacentes são iguais.
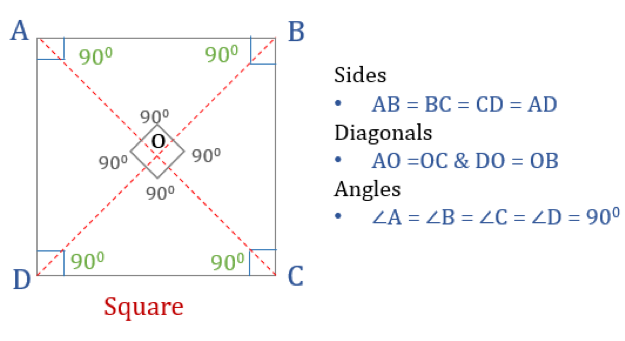
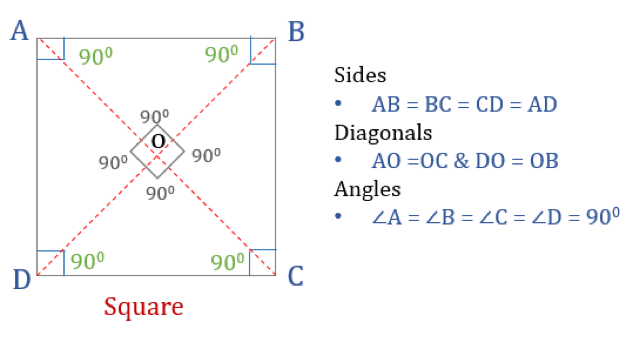
Propriedades de um quadrado
Para que um quadrilátero seja um quadrado, ele tem que ter certas propriedades. Aqui estão as três propriedades do quadrado:
- Todos os ângulos de um quadrado são 90°
- Todos os lados de um quadrado são iguais e paralelos uns aos outros
- Diagonais bissetam-se perpendicularmente
Fórmula do quadrado – Área e perímetro de um quadrado
Se o lado de um quadrado é ‘a’ então,
- Área do quadrado = a × a = a²
- Perímetro do quadrado = 2 × (a + a) = 4a
Estas questões práticas irão ajudá-lo a solidificar as propriedades dos quadrados
Scoring a Q50-51 no GMAT ajuda-o a obter uma pontuação de 700+ GMAT. Por que você não começa a se preparar para o GMAT com nossos recursos gratuitos de preparação e começa sua jornada para obter uma Q50-51 sobre o GMAT. Aprenda com Carrie Law que melhorou de Q35 para Q50 em 3 semanas.
Parallelograma
Um paralelogramo, como o nome sugere, é um simples quadrilátero cujos lados opostos são paralelos. Assim, ele tem dois pares de lados paralelos. Além disso, os ângulos opostos de um paralelogramo são iguais e suas diagonais se bissetam.
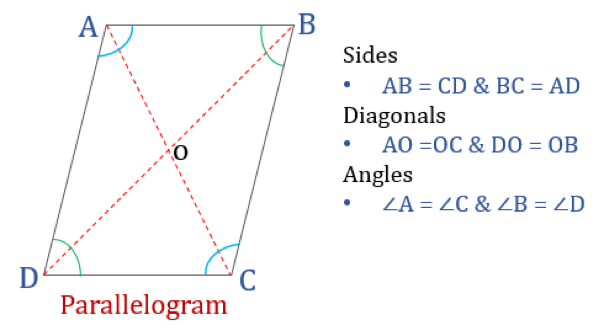
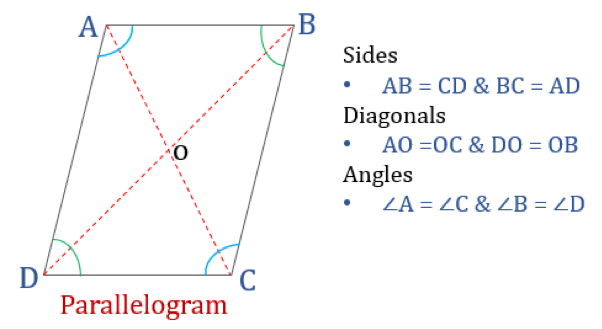
Propriedades de paralelogramo
Um quadrilátero que satisfaça as propriedades abaixo mencionadas será classificado como um paralelogramo. Um paralelogramo tem quatro propriedades:
- Ângulos dopposite são iguais
- Lados dopposite são iguais e paralelos
- Diagonais se bissecam
- Soma de quaisquer dois ângulos adjacentes é 180°
Fórmulas de paralelogramo – Área e perímetro de um paralelogramo
Se o comprimento de um paralelogramo for ‘l’, A largura é ‘b’ e a altura é ‘h’ então:
- Perímetro do paralelogramo= 2 × (l + b)
- Área do paralelogramo = l × h
Estas perguntas práticas irão ajudá-lo a solidificar as propriedades do paralelogramo
Rhombus
Um losango é um quadrilátero cujos quatro lados são iguais em comprimento e lados opostos são paralelos um ao outro. No entanto, os ângulos não são iguais a 90°. Um losango com ângulos retos se tornaria um quadrado. Outro nome para losango é ‘diamante’ pois parece similar ao naipe de diamante nas cartas de jogo.
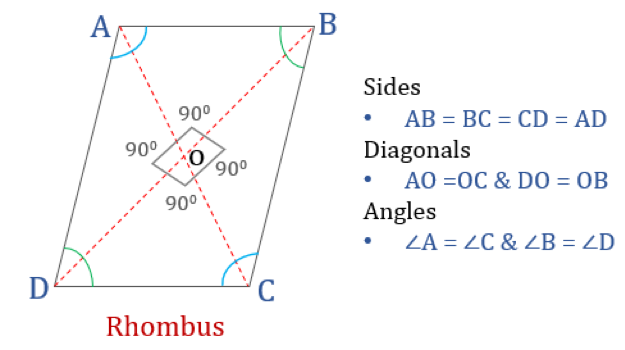
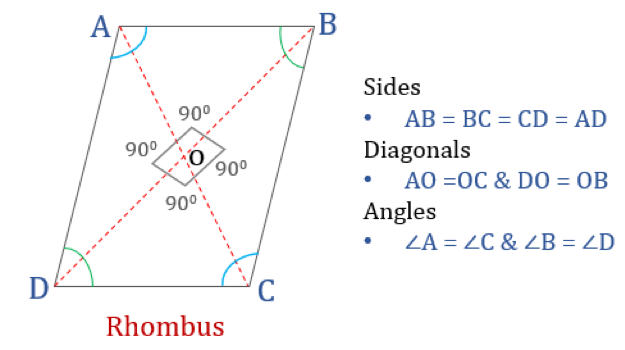
Propriedades do losango
Um losango é um quadrilátero que tem as quatro propriedades seguintes:
- Ângulos do oponente são iguais
- Todos os lados são iguais e, lados opostos são paralelos uns aos outros
- Diagonais bissetam-se perpendicularmente
- Soma de quaisquer dois ângulos adjacentes é 180°
Fórmulas de losango – Área e perímetro de um losango
Se o lado de um losango é um então, perímetro de um losango = 4a
Se o comprimento de duas diagonais do losango for d1 e d2 então a área de um losango = ½ × d1 × d2
Estas questões práticas irão ajudam a solidificar as propriedades do losango
Trapézio
Um trapézio (chamado Trapézio nos EUA) é um quadrilátero que tem apenas um par de lados paralelos. Os lados paralelos são chamados de ‘bases’ e os outros dois lados são chamados de ‘pernas’ ou lados laterais.
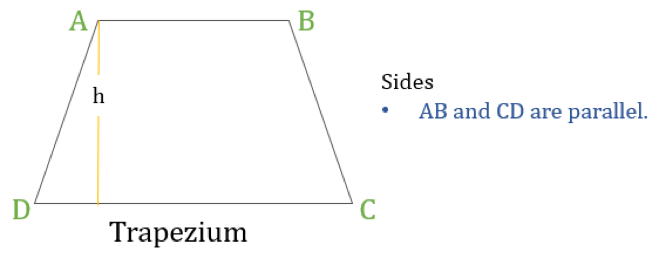
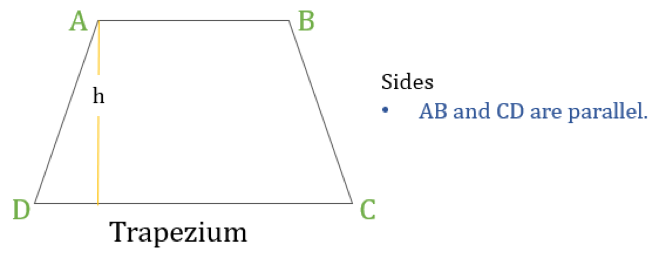
Propriedades do Trapézio
Um trapézio é um quadrilátero no qual a seguinte propriedade:
- Apenas um par de lados opostos são paralelos um ao outro
Fórmulas do trapézio – Área e perímetro de um trapézio
Se a altura de um trapézio é ‘h’ (como mostrado no diagrama acima) então:
- Perímetro do trapézio = Soma dos comprimentos de todos os lados = AB + BC + CD + DA
- Área do trapézio = ½ × (Soma dos comprimentos dos lados paralelos) × h = ½ × (AB + CD) × h
Estas questões práticas irão ajudá-lo a solidificar as propriedades do trapézio
Propriedades dos quadriláteros
A tabela abaixo resume todas as propriedades dos quadriláteros que aprendemos até agora:
| Propriedades dos quadriláteros | Rectângulo | Quadrado | Parallelograma | Rhombus | Trapézio |
| Todos os lados são iguais | ✖ | ✔ | ✖ | ✔ | ✖ |
| Opposite Os lados são iguais | ✔ | ✔ | ✔ | ✔ | ✖ |
| Opposite Os lados são paralelos | ✔ | ✔ | ✔ | ✔ | ✔ |
| Todos os ângulos são iguais | ✔ | ✔ | ✖ | ✖ | ✖ |
| Ângulos do opposite são iguais | ✔ | ✔ | ✔ | ✔ | ✖ |
| Soma de dois ângulos adjacentes é 180 | ✔ | ✔ | ✔ | ✔ | ✖ |
| Bisectar um ao outro | ✔ | ✔ | ✔ | ✔ | ✖ |
| Bisectar perpendicularmente | ✖ | ✔ | ✖ | ✔ | ✖ |
A imagem abaixo também resume as propriedades dos quadriláteros:
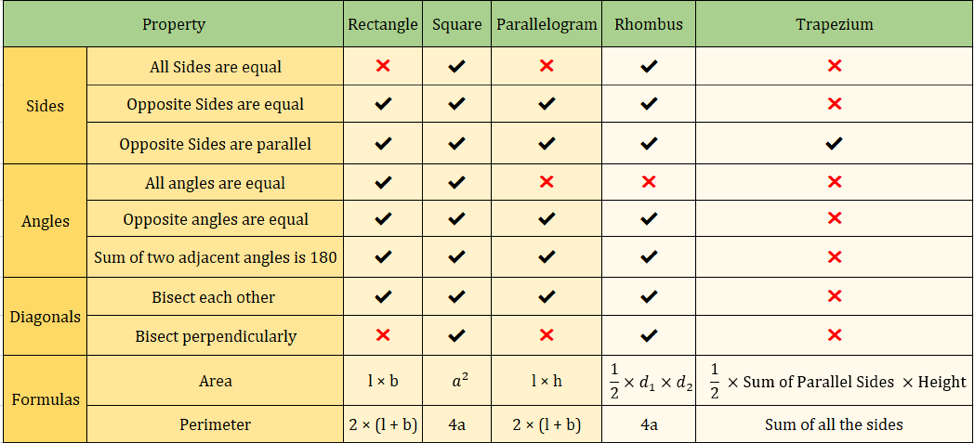
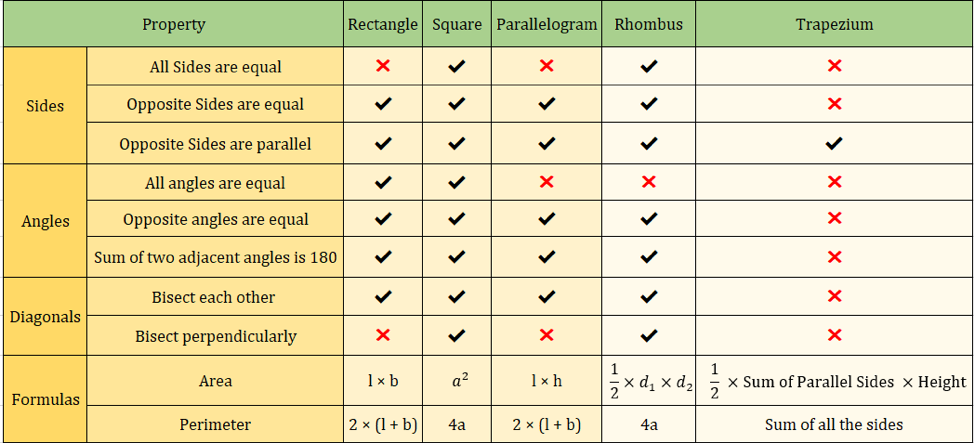
Fórmulas importantes de quadriláteros
A tabela abaixo resume as fórmulas em área e perímetro dos diferentes tipos de quadriláteros:
| Fórmulas quadriláteras | Rectângulo | Quadrado | Parallelograma | Rhombus | Trapézio |
| Area | l × b | a² | l × h | ½ × d1 × d2 | ½ × (Soma dos lados paralelos) × altura |
| Perímetro | 2 × (l + b) | 4a | 2 × (l + b) | 4a | Soma de todos os lados |
Outra leitura:
- Propriedades de Círculo | Fórmulas de Círculo – Área e Perímetro
- Propriedades de Números – Mesmo & Ímpar | Prime | HCF & LCM
- Propriedades de Triângulos – Definição | Tipos | Classificação
- Linhas e ângulos – Propriedades e sua Aplicação
Quadrilaterais
Vamos praticar a aplicação das propriedades dos quadriláteros nas seguintes questões da amostra:
Question 1
Adam quer construir uma cerca à volta do seu jardim rectangular de 10 metros de comprimento e 15 metros de largura. Quantos metros da cerca ele deve comprar para cercar todo o jardim?
- 20 metros
- 25 metros
- 30 metros
- 40 metros
- 50 metros
Solução
Passo 1: Dado
- Adam tem um jardim retangular.
- Tem um comprimento de 10 metros e uma largura de 15 metros.
- Ele quer construir uma cerca em torno dele.
Passo 2: Encontrar
- O comprimento necessário para construir a cerca em torno de todo o jardim.
- Então, o comprimento total da vedação necessária= Soma dos comprimentos de todos os lados do jardim.
- Desde que o jardim é rectangular, a soma do comprimento de todos os lados não é mais do que o perímetro do jardim.
- Perímetro = 2 × (10 + 15) = 50 metros
Passo 3: Aproximação e Trabalho para fora
A vedação só pode ser construída ao redor dos lados exteriores do jardim.
A cerca, o comprimento requerido da cerca é de 50 metros.
Por isso, a opção E é a resposta correcta.
Pergunta: 2
Steve quer pintar uma parede de forma rectangular do seu quarto. O custo para pintar a parede é de $1,5 por metro quadrado. Se a parede tem 25 metros de comprimento e 18 metros de largura, então qual é o custo total para pintar a parede?
- $ 300
- $ 350
- $ 450
- $ 600
- $ 675
Solução
Passo 1: Dado
- Steve quer pintar uma parede do seu quarto.
- A parede tem 25 metros de comprimento e 18 metros de largura.
- Custo para pintar a parede é $1,5 por metro quadrado.
Passo 2: Encontrar
>
- O custo total para pintar a parede.
Passo 3: Aproximação e Trabalho para fora
- Uma parede é pintada em toda a sua área.
- Então, se encontrarmos a área total da parede em metros quadrados e multiplicá-la pelo custo para pintar 1 metro quadrado da parede, então podemos o custo total.
- Área da parede = comprimento × Largura = 25 metros × 18 metros = 450 metros quadrados
- Custo total para pintar a parede = 450 × $1.5 = $675
Hence, a resposta correta é a opção E.
Esperamos que você já tenha aprendido os diferentes tipos de quadriláteros, suas propriedades e fórmulas e como aplicar estes conceitos para resolver questões sobre quadriláteros. A aplicação de quadriláteros é importante para resolver questões de geometria sobre o GMAT. Se você está planejando tomar o GMAT, nós podemos ajudá-lo com material de estudo de alta qualidade que você pode acessar gratuitamente registrando-se aqui.
Aqui estão mais alguns artigos sobre Matemática:
- Melhorar a precisão em questões de Matemática em Polígonos
- Perguntas de Geometria – Erros Mais Comuns | GMAT Quant Prep
Se você está planejando tomar o GMAT, nós podemos lhe dar acesso a conteúdo online de qualidade para se preparar. Somos a empresa de preparação GMAT mais revista no gmatclub com mais de 1950 revisões.
Por que você não faz um julgamento gratuito e julga por si mesmo?
Escreva-nos em [email protected] no caso de qualquer consulta.




