Skewness – Introdução Rápida, Exemplos & Fórmulas
Skewness é um número que indica até que ponto
uma variável está assimetricamente distribuída.
- Positivo (Direita) Skewness Exemplo
- Negativo (Esquerda) Skewness Exemplo
- População Skewness – Fórmula e Cálculo
- Amostras de Skewness – Fórmula e Cálculo
- Skewness em SPSS
- Skewness – Implicações para Análise de Dados
>
Positivo (Direita) Exemplo de Skewness
Um cientista tem 1,000 pessoas completam alguns testes psicológicos. Para o teste 5, os resultados do teste têm uma inclinação = 2,0. Um histograma destes resultados é mostrado abaixo.
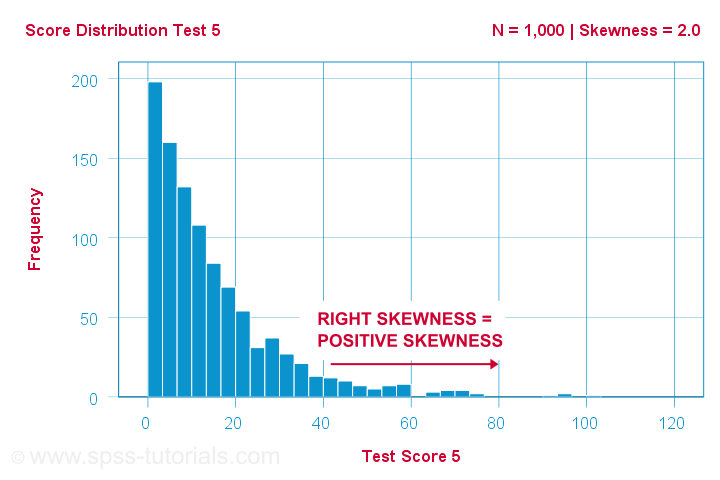
O histograma mostra uma distribuição de frequência muito assimétrica. A maioria das pessoas tem 20 pontos ou menos, mas a cauda direita estica-se até cerca de 90. Esta distribuição é inclinada para a direita.
Se nos movermos para a direita ao longo do eixo x, passamos de 0 a 20 a 40 pontos e assim por diante. Assim, para a direita do gráfico, as pontuações tornam-se mais positivas. Portanto, o enviesado à direita é enviesado positivo, o que significa enviesado > 0. Este primeiro exemplo tem enviesado = 2,0 como indicado no canto superior direito do gráfico. As pontuações são fortemente inclinadas positivamente.
Negativa (Esquerda) Skewness Exemplo
Outra variável – as pontuações no teste 2- acabam por ter skewness = -1.0. O histograma deles é mostrado abaixo.

A maior parte das pontuações está entre 60 e 100 ou mais. No entanto, a cauda esquerda é um pouco esticada. Portanto, esta distribuição é inclinada para a esquerda.
Direita: para a esquerda, para a esquerda. Se seguirmos o eixo x para a esquerda, avançamos para pontuações mais negativas. É por isso que o enviesado para a esquerda é enviesado negativo. E de fato, enviesado = -1.0 para estas pontuações. A sua distribuição é inclinada para a esquerda. Entretanto, é menos enviesada – ou mais simétrica – do que nosso primeiro exemplo que teve enviesamento = 2.0.
Distribuição simétrica Implica enviesamento zero
Finalmente, distribuições simétricas têm enviesamento = 0. As pontuações no teste 3 – tendo enviesamento = 0.1- se aproximam.

Agora, as distribuições observadas raramente são precisamente simétricas. Isto é visto principalmente para algumas distribuições teóricas de amostragem. Alguns exemplos são
- a distribuição normal (padrão);
- a distribuição t e
- a distribuição binomial se p = 0.5.
Estas distribuições são todas exatamente simétricas e, portanto, têm obliquidade = 0.000…
População Skewness – Fórmula e Cálculo
Se você quiser computar skewnesses para uma ou mais variáveis, deixe os cálculos para algum software. Mas – só para completar – eu vou listar as fórmulas de qualquer maneira.
Se os seus dados contêm toda a sua população, calcule o skewness da população como:
$$População;skewness = {X_i -mu}{sigma}{X_i -mu}{\i}biggr)^3^cdot{1}frac{N}$$
onde
- (X_i}) é cada pontuação individual;
- >(N) é a média da população;
- (N) é o desvio padrão da população e
- (N) é o tamanho da população.
Para um exemplo de cálculo usando esta fórmula, veja esta folha de Googles (mostrada abaixo).
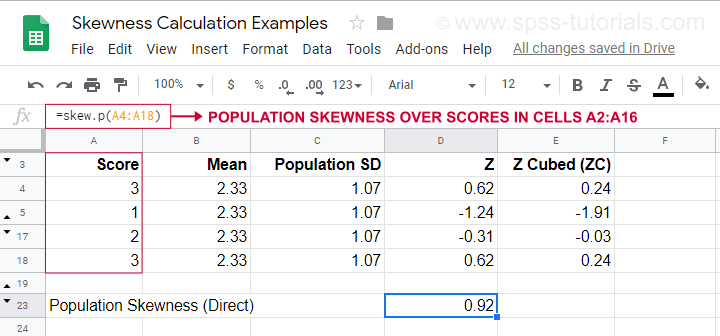
Mostra também como obter o enviesamento populacional diretamente usando=SKEW.P(…) onde “.P” significa “população”. Isto confirma o resultado do nosso cálculo manual. Infelizmente, nem o SPSS nem o JASP calculam o enviesamento populacional: ambos se limitam à amostra de enviesamento.
Espessura da amostra – Fórmula e Cálculo
Se os seus dados contêm uma amostra aleatória simples de alguma população, use
$$Amostra\;skewness = \frac{N\cdot\Sigma(X_i – {X})^3}{S^3(N – 1)(N – 2)}$$
where
- \(X_i}) é cada pontuação individual;
- (X) é a média da amostra;
- (S) é o desvio padrão da amostra e
- (N) é o tamanho da amostra.
Um exemplo de cálculo é mostrado nesta folha de Googles (mostrada abaixo).
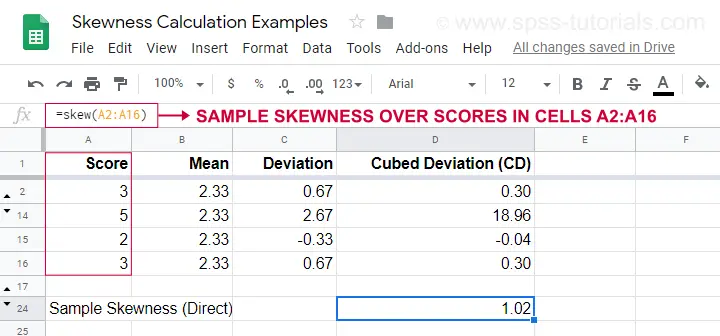
Uma opção mais fácil para a obtenção de amostra skewness é usar=SKEW(…).que confirma o resultado do nosso cálculo manual.
Skewness no SPSS
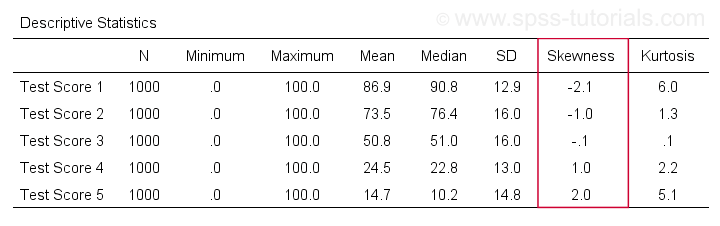
Primeiro off, “skewness” no SPSS refere-se sempre a skewness de amostra: assume-se calmamente que os seus dados contêm uma amostra em vez de uma população inteira. Há muitas opções para obtê-lo. O meu favorito é via MEANS porque a sintaxe e a saída são limpas e simples. Os screenshots abaixo guiam você através de.

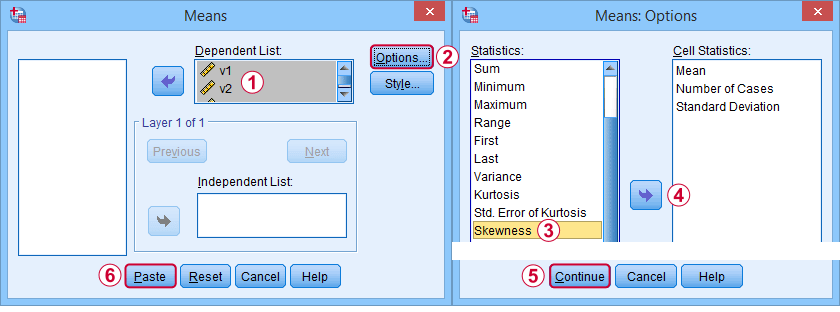
A sintaxe pode ser tão simples quanto os meios v1 a v5
/cells skew.Uma tabela muito completa -incluindo médias, desvios padrão, medianas e mais- é executada dos meios v1 a v5
/cells count min max median stddev skew kurt.O resultado é mostrado abaixo.
Skewness – Implicações para Análise de Dados
Muitas análises -ANOVA, testes t, regressão e outras – requerem a suposição de normalidade: as variáveis devem ser normalmente distribuídas na população. A distribuição normal tem enviesamento = 0. Assim, a observação de enviesamento substancial em alguns dados da amostra sugere que a suposição de normalidade é violada.
Suas violações de normalidade não são problema para amostras de tamanho grande -diga N > 20 ou 25 ou mais. Neste caso, a maioria dos testes são robustos contra tais violações. Isto é devido ao teorema do limite central. Em resumo, para amostras grandes, o enviesamento é
nenhum problema real para testes estatísticos. No entanto, o enviesamento está frequentemente associado a grandes desvios padrão. Estes podem resultar em grandes erros-padrão e baixo poder estatístico. Assim, uma assimetria substancial pode diminuir a chance de rejeitar alguma hipótese nula a fim de demonstrar algum efeito. Neste caso, um teste não-paramétrico pode ser uma escolha mais sábia, pois pode ter mais poder. As violações da normalidade representam uma ameaça real
para amostras de tamanho pequeno de -say- N < 20 ou mais. Com amostras de tamanho pequeno, muitos testes não são robustos contra uma violação da suposição de normalidade. A solução – mais uma vez – está usando um teste não paramétrico porque estes não requerem normalidade.
Primeiro mas não menos importante, não há nenhum teste estatístico para examinar se a inclinação da população = 0. Uma forma indireta de testar isto é um teste de normalidade como
- o teste de normalidade de Kolmogorov-Smirnov e
- o teste de normalidade de Shapiro-Wilk.
No entanto, quando a normalidade é realmente necessária – com amostras pequenas – esses testes têm baixa potência: eles podem não alcançar significância estatística mesmo quando os desvios da normalidade são severos. Desta forma, eles fornecem principalmente uma falsa sensação de segurança.




