Interpretarea coeficienților de regresie liniară

Învățați cum să interpretați corect rezultatele regresiei liniare – inclusiv cazurile cu transformări ale variabilelor
În prezent există o multitudine de algoritmi de învățare automată pe care îi putem încerca pentru a găsi cel mai potrivit pentru problema noastră particulară. Unii dintre algoritmi au o interpretare clară, alții funcționează ca o cutie neagră și putem folosi abordări precum LIME sau SHAP pentru a obține unele interpretări.
În acest articol, aș dori să mă concentrez asupra interpretării coeficienților celui mai de bază model de regresie, și anume regresia liniară, inclusiv asupra situațiilor în care variabilele dependente/independente au fost transformate (în acest caz mă refer la transformarea logaritmică).
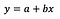
Presupun că cititorul este familiarizat cu regresia liniară (dacă nu, există o mulțime de articole bune și postări pe Medium), așa că mă voi concentra doar pe interpretarea coeficienților.
Formula de bază pentru regresia liniară poate fi văzută mai sus (am omis intenționat reziduurile, pentru a păstra lucrurile simple și la obiect). În formulă, y desemnează variabila dependentă, iar x este variabila independentă. Pentru simplitate, să presupunem că este vorba de o regresie univariată, dar principiile sunt valabile, în mod evident, și pentru cazul multivariat.
Pentru a pune lucrurile în perspectivă, să spunem că după ajustarea modelului primim:
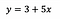
Intercept (a)
Voi împărți interpretarea conceptului de interceptare în două cazuri:
- x este continuă și centrată (prin scăderea mediei lui x din fiecare observație, media lui x transformată devine 0) – media y este 3 când x este egală cu media eșantionului
x este continuă, dar nu este centrat – media y este 3 atunci când x = 0 x este categorică – media y este 3 atunci când x = 0 (de data aceasta indicând o categorie, mai multe despre aceasta mai jos)
Coeficient (b)
- x este o variabilă continuă
Interpretare: o creștere de o unitate a lui x determină o creștere a mediei y cu 5 unități, toate celelalte variabile rămânând constante.
- x este o variabilă categorică
Aceasta necesită un pic mai multe explicații. Să spunem că x descrie sexul și poate lua valori („bărbat”, „femeie”). Acum să o transformăm într-o variabilă fictivă care ia valorile 0 pentru bărbați și 1 pentru femei.
Interpretare: media y este mai mare cu 5 unități pentru femei decât pentru bărbați, toate celelalte variabile rămânând constante.
model la nivel de logaritm
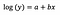
În mod obișnuit, folosim transformarea logaritmică pentru a apropia datele periferice dintr-o distribuție cu înclinație pozitivă de cea mai mare parte a datelor, pentru a face variabila distribuită normal. În cazul regresiei liniare, un beneficiu suplimentar al utilizării transformării logaritmice este interpretabilitatea.
Ca și înainte, să spunem că formula de mai jos prezintă coeficienții modelului ajustat.
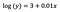
Intercept (a)
Interpretarea este similară cu cea din cazul vanilă (la nivel de nivel), însă, pentru interpretare, trebuie să luăm exponentul interceptului exp(3) = 20,09. Diferența constă în faptul că această valoare reprezintă media geometrică a lui y (spre deosebire de media aritmetică în cazul modelului la nivel de nivel).
Coeficient (b)
Principiile sunt din nou similare cu cele ale modelului la nivel de nivel atunci când vine vorba de interpretarea variabilelor categorice/numerice. În mod analog cu interceptul, trebuie să luăm exponentul coeficientului: exp(b) = exp(0,01) = 1,01. Acest lucru înseamnă că o creștere unitară a lui x determină o creștere cu 1% a valorii medii (geometrice) a lui y, toate celelalte variabile rămânând constante.
Două lucruri merită menționate aici:
- Există o regulă de bază atunci când vine vorba de interpretarea coeficienților unui astfel de model. Dacă abs(b) < < 0,15 este destul de sigur să spunem că atunci când b = 0,1 vom observa o creștere de 10% în y pentru o schimbare unitară în x. Pentru coeficienții cu valoare absolută mai mare, se recomandă calcularea exponentului.
Când avem de-a face cu variabile în interval (cum ar fi un procent) este mai convenabil pentru interpretare să înmulțim mai întâi variabila cu 100 și apoi să ajustăm modelul. În acest fel, interpretarea este mai intuitivă, deoarece creștem variabila cu 1 punct procentual în loc de 100 de puncte procentuale (de la 0 la 1 imediat).
model level-log
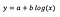
Să presupunem că după ajustarea modelului primim:

Interpretarea coordonatei de interceptare este aceeași ca în cazul modelului la nivel de nivel.
Pentru coeficientul b – o creștere de 1% în x are ca rezultat o creștere aproximativă a mediei y cu b/100 (0,05 în acest caz), toate celelalte variabile rămânând constante. Pentru a obține valoarea exactă, ar trebui să luăm b× log(1,01), care în acest caz dă 0,0498.
model log-log
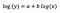
Să presupunem că după ajustarea modelului primim:
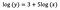
Încă o dată mă concentrez pe interpretarea lui b. O creștere a lui x cu 1% duce la o creștere cu 5% a mediei (geometrice) y, toate celelalte variabile rămânând constante. Pentru a obține suma exactă, trebuie să luăm
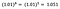
ceea ce reprezintă ~5,1%.
Concluzii
Sper că acest articol v-a oferit o imagine de ansamblu asupra modului de interpretare a coeficienților de regresie liniară, inclusiv în cazurile în care unele dintre variabile au fost transformate în logaritmi. Ca întotdeauna, orice feedback constructiv este binevenit. Puteți să mă contactați pe Twitter sau în comentarii.
.




