Metoda diviziunii sintetice
Trebuie să spun că diviziunea sintetică este cea mai „distractivă” metodă de împărțire a polinoamelor. Are mai puțini pași pentru a ajunge la răspuns în comparație cu metoda împărțirii lungi a polinoamelor. În această lecție, voi trece în revistă cinci (5) exemple care ar trebui, sper, să vă familiarizeze cu procedurile de bază în împărțirea cu succes a polinoamelor folosind împărțirea sintetică.
Ce lucruri de reținut:
- Asigurați-vă că dividendul este în formă standard. Asta înseamnă că puterile sunt în ordine descrescătoare.
- Divizorul trebuie să fie de forma x – \stânga( c \dreapta).
Exemple de împărțire a polinoamelor folosind diviziunea sintetică
Exemplu 1: Să împărțim polinomul de mai jos.
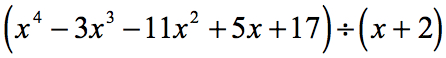
Să reanalizăm problema dată și să facem ajustările necesare, dacă este cazul.
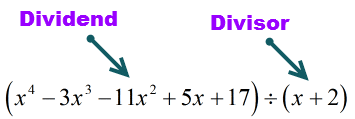
Divizatul (materia de împărțit) este în formă standard deoarece exponenții sunt în ordine descrescătoare. Asta e bine!
Divizorul trebuie rescris sub forma
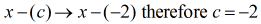
În acest moment, pot acum să configurez diviziunea sintetică prin extragerea coeficienților dividendului și apoi alinierea lor deasupra.
Direct în partea stângă, plasez valoarea lui c = – 2 în interiorul „cutiei”.
În final, construiesc o linie orizontală chiar sub coeficienții dividendului.
Etapele:
1. Aruncați primul coeficient sub linia orizontală.
2. Înmulțițiți acel număr pe care l-ați aruncat cu numărul din „căsuță”. Oricare ar fi produsul său, puneți-l deasupra liniei orizontale, chiar sub al doilea coeficient.
3. Adunați coloana de numere, apoi puneți suma direct sub linia orizontală.
4. Repetați procesul până când nu mai aveți coloane de adăugat.
Vezi soluția animată de mai jos:
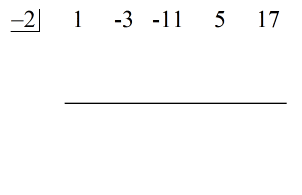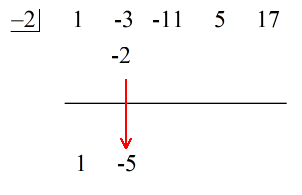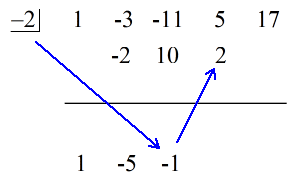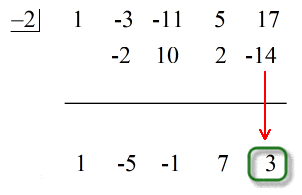
Ultimul număr de sub linia orizontală este întotdeauna restul! Restul acestei probleme este 3.
Atunci cum prezentăm răspunsul final?
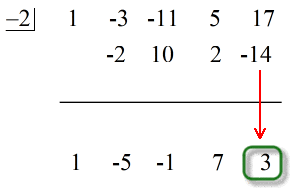
- Prezentați răspunsul final sub forma
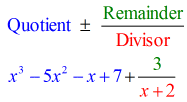
Observați că numerele de sub linia orizontală, cu excepția ultimului (restul), sunt coeficienții coeficientului Corespunzător.
Mai mult, exponenții variabilelor din coeficient sunt toți reduși cu 1.
Exemplul 2: Împărțiți polinomul.
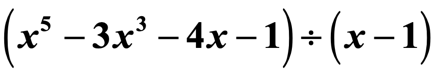
Aceasta nu este o întrebare capcană. Observați că în cvorbitor nu se află toți exponenții variabilei x.
Văd că ne lipsesc {x^4} și {x^2}. Pentru a include toți coeficienții variabilei x în putere descrescătoare, ar trebui să rescriem problema inițială astfel. Atașați zerouri pe acei x lipsă. De asemenea, să exprimăm divizorul ca x – (c), ceea ce relevă clar valoarea lui c, adică c = + 1.
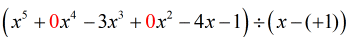
Din acest punct, pot acum să stabilesc numerele pentru a continua procesul.
Etapele:
1. Aruncați primul coeficient sub linia orizontală.
2. Înmulțițiți acel număr pe care l-ați aruncat cu numărul din „cutie”. Oricare ar fi produsul său, puneți-l deasupra liniei orizontale, chiar sub al doilea coeficient.
3. Adunați coloana de numere, apoi puneți suma direct sub linia orizontală.
4. Repetați procesul până când nu mai aveți coloane de adăugat.
Vezi soluția animată de mai jos:
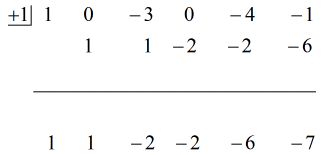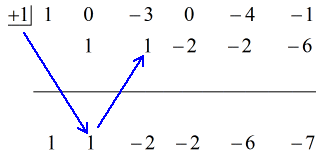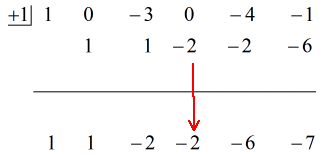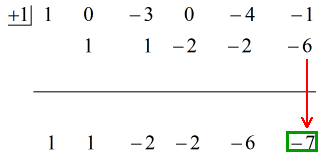
Atunci punând răspunsul final sub forma
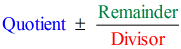
avem
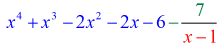
Exemplul 3: Împărțiți polinomul de mai jos.
\left( { – 2{x^4} + x} \right) \div \left( {x – 3} \right)
Acest lucru devine din ce în ce mai interesant! Cotientul arată cu siguranță oribil pentru că lipsește foarte mult. Nu numai că îi lipsesc niște x care sunt {x^3} și {x^2}, dar a dispărut și constanta.
Pentru a rezolva acest lucru, voi rescrie problema inițială în așa fel încât să fie luate în calcul toate x-urile. Dar, mai important, nu uitați să includeți constanta lipsă care este zero.
Problema „nouă și îmbunătățită” ar trebui să arate astfel:
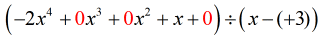
De aici, continuați cu pașii ca de obicei.
Pași:
1. Aruncați primul coeficient sub linia orizontală.
2. Înmulțiți acel număr pe care l-ați aruncat cu numărul din „cutie”. Oricare ar fi produsul său, puneți-l deasupra liniei orizontale, chiar sub al doilea coeficient.
3. Adunați coloana de numere, apoi puneți suma direct sub linia orizontală.
4. Repetați procesul până când nu mai aveți coloane de adăugat.
Vezi soluția animată de mai jos:
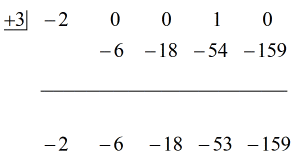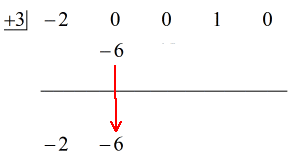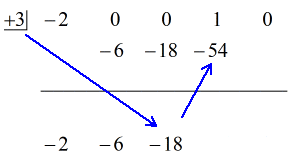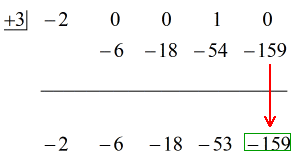
Bine atunci, răspunsul final pentru acest lucru este
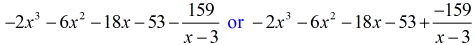
Puteți scrie răspunsul final în două moduri. Primul este folosind simbolul minus sau simbolul de scădere pentru a indica faptul că restul este negativ. Al doilea constă în utilizarea simbolului +, dar atașând un simbol negativ la numărător. Ele înseamnă același lucru!
Exemplul 4: Împărțiți polinomul de mai jos.
\left( { – {x^5} + 1} \right) \div \left( {x + 1} \right)
Nu vă lăsați descurajați de această problemă. Aceasta este de fapt destul de ușoară, mai ales acum că ați parcurs deja câteva exemple. Amintiți-vă întotdeauna să „completați părțile lipsă”, nu-i așa?
Observați dividendul și ar trebui să fiți de acord că părțile lipsă sunt {x^4}, {x^3}, {x^2} și x.
Scriind din nou problema inițială care este pregătită pentru împărțirea sintetică, obținem…
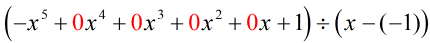
Să populăm x-urile lipsă cu zerouri și să rezolvăm explicit pentru c = -1.
Etapele:
1. Aruncați primul coeficient sub linia orizontală.
2. Înmulțițiți acel număr pe care l-ați aruncat cu numărul din „cutie”. Oricare ar fi produsul său, puneți-l deasupra liniei orizontale, chiar sub al doilea coeficient.
3. Adunați coloana de numere, apoi puneți suma direct sub linia orizontală.
4. Repetați procesul până când nu mai aveți coloane de adăugat.
Vezi soluția animată de mai jos:
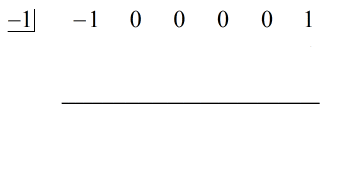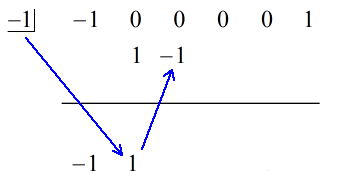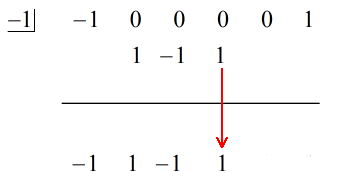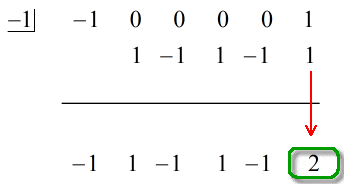
Ultimul număr de sub linia orizontală va fi întotdeauna restul. Nu uitați că. În acest caz, restul este egal cu 2.
Răspunsul nostru final este
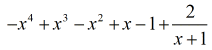
Exemplul 5: Împărțiți polinomul cu un binom.
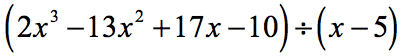
În acest exemplu, vom obține un rest egal cu zero. Când se întâmplă acest lucru, divizorul devine un factor al dividendului. Cu alte cuvinte, divizorul împarte în mod egal dividendul.
Examinând problema, văd că nu există componente lipsă. Toate puterile lui x sunt luate în considerare și avem o constantă. Asta este minunat! Această problemă este de fapt pregătită pentru împărțirea sintetică.
Etapele:
1. Aruncați primul coeficient sub linia orizontală.
2. Înmulțițiți acel număr pe care l-ați aruncat cu numărul din „cutie”. Oricare ar fi produsul său, puneți-l deasupra liniei orizontale, chiar sub al doilea coeficient.
3. Adunați coloana de numere, apoi puneți suma direct sub linia orizontală.
4. Repetați procesul până când nu mai aveți coloane de adăugat.
Vezi soluția animată de mai jos:
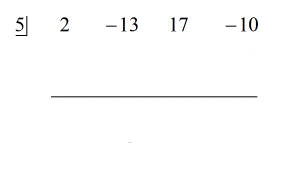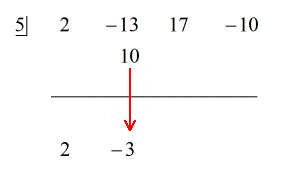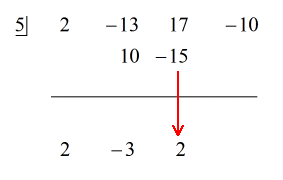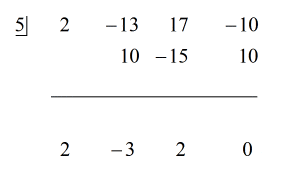
Pentru că restul este egal cu zero, aceasta înseamnă că divizorul x – 5 este un factor al dividendului
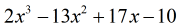
De aceea
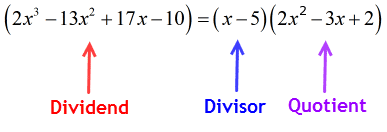
Practicați cu fișe de lucru
S-ar putea să vă intereseze și:
Puteți fi interesați și de:
Sumarea și scăderea polinoamelor
Divizarea polinoamelor folosind metoda diviziunii lungi
Multiplicarea binomelor folosind metoda FOIL
Multiplicarea polinoamelor
.




