Probabilități Introducere: Articole și videoclipuri cu soluții!
 Rularea zarurilor, găsirea unui loc de parcare, câștig la cărți; Acestea sunt doar câteva situații în care ați putea dori să aflați care sunt șansele ca un eveniment să se întâmple. Dacă doriți să știți cum să găsiți probabilitatea, trebuie mai întâi să vă dați seama ce fel de întrebare aveți. De exemplu, modul în care găsiți șansele ca un eveniment să se întâmple este diferit de găsirea șanselor ca membrii unui grup să aleagă același lucru.
Rularea zarurilor, găsirea unui loc de parcare, câștig la cărți; Acestea sunt doar câteva situații în care ați putea dori să aflați care sunt șansele ca un eveniment să se întâmple. Dacă doriți să știți cum să găsiți probabilitatea, trebuie mai întâi să vă dați seama ce fel de întrebare aveți. De exemplu, modul în care găsiți șansele ca un eveniment să se întâmple este diferit de găsirea șanselor ca membrii unui grup să aleagă același lucru.
Câteva probabilități sunt ușor de identificat, cum ar fi găsirea probabilităților de aruncare a zarurilor sau de alegere dintr-un pachet de cărți.
Întrebările care implică teorema binomială sunt, de asemenea, ușor de identificat. În aceste tipuri de experimente, singurele rezultate posibile ale unui eveniment sunt „Succes” sau „Eșec”: cum ar fi da/nu, cap/coadă sau alb/negru.
Alte tipuri de întrebări pe care le-ați putea întâlni implică oameni, cum ar fi:
- Selectarea unei persoane dintr-un grup sau comitet.
- Probabilitatea ca un grup să aleagă același lucru.
Evenimente
Vreți să aflați probabilitatea ca un eveniment simplu să se întâmple? Cum ar fi să plouă sau să găsiți un loc de parcare în centrul orașului? Vedeți:
Probabilitatea ca un eveniment simplu să se întâmple.
Pe de altă parte, dacă doriți exact opusul, vedeți:
Cum să aflați probabilitatea ca un eveniment să NU se întâmple.
Întrebarea dvs. se referă la faptul că un eveniment se întâmplă având în vedere un alt eveniment? Cum ar fi probabilitatea de a găsi un loc de parcare, având în vedere că este zi de meci, sau de a găsi o anumită jucărie populară de Black Friday? Dacă da, verificați:
- Șansele unui eveniment, dat fiind un alt eveniment.
- Două evenimente care au loc împreună.
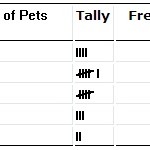
Un tabel de distribuție a frecvențelor.
Distribuții de frecvențe
Aveți o distribuție de frecvențe cu care să lucrați? Sau sunteți în măsură să realizați un tabel de distribuție a frecvențelor cu datele date? De exemplu, aveți un număr x de articole cu anumite trăsături. Distribuția de frecvență a probabilităților.
Introducere la probabilități: Articole și videoclipuri practice.
- Permutații și combinații: Cum se rezolvă probleme
- Probleme de probabilitate: Rezolvați-le în mod simplu!
- Probabilitatea lui a și b.
- Regula probabilității totale.
- Probleme cu teorema lui Bayes: Pași simpli de rezolvare.
- Probabilitatea anterioară (inclusiv neinformativă și conjugată).
- Cum se face o distribuție de probabilitate din date.
- Cum se găsește probabilitatea de a selecta o persoană dintr-un grup sau comitet.
- Cum se găsește probabilitatea ca un eveniment să NU se întâmple.
- Distribuția probabilității de frecvență.
- Cum se găsește probabilitatea ca un eveniment simplu să se întâmple.
- Eveniment aleator: Probabilitatea dat fiind un procent.
- Cum se găsește probabilitatea ca membrii unui grup să aleagă același lucru.
- Cum se găsește probabilitatea ca două evenimente dependente să se întâmple împreună.
- Cum se găsește probabilitatea ca un eveniment să se întâmple, dat fiind un alt eveniment.
- Cum să utilizați un arbore de probabilitate (arbore de decizie) pentru a calcula șansele.
- Cum să aflați probabilitatea de a extrage o carte dintr-un pachet.
- Cum să vă dați seama dacă ceva este un eveniment care se exclude reciproc.
- Cum să faceți diferența între evenimente dependente și independente.
- Probabilitate: Aruncarea zarurilor.
- Cum să desenezi o diagramă Venn.
- Cum să creezi o diagramă Euler.
- 5 alege 3: cum să rezolvi combinații.
- Cum să folosești principiul fundamental de numărare.
- Cum să găsești valoarea așteptată pentru o variabilă aleatoare discretă.
Introducere la probabilități: Definiții
- Probabilitatea axiomatică.
- Legea lui Benford
- Ce este un experiment binomial?
- Ratele de bază și Falsitatea ratei de bază
- Scurturile lui Brier
- Exhaustivitatea colectivă
- Ce sunt combinațiile?
- Evenimentele complementare.
- Așteptarea condiționată
- Ce este frecvența relativă condiționată?
- Additivitatea numărabilă
- Set gol
- Probabilitate epistemică
- Spații de evenimente.
- Ce este probabilitatea experimentală?
- Distribuții de probabilitate comune.
- Distribuție limită.
- Estimare de maximă verosimilitate
- Proprietatea fără memorie.
- Metoda Monte Carlo.
- Problema lui Monty Hall
- Ce este un eveniment mutual exclusiv?
- Ce este un eveniment mutual inclusiv?
- Ce este un eveniment mutual inclusiv?
- Mutually Independent și Pairwise Independent.
- Ce este regula înmulțirii?
- Nash Equilibrium
- Nonempty Set
- Normal Probability Practice Problems.
- Ce este un grafic de probabilitate normală?
- Probabilitate obiectivă
- Ce este raportul de probabilitate?
- Analiză predictivă
- Ce este un tabel de distribuție a probabilităților?
- Măsură de probabilitate
- Ce este un spațiu de probabilitate?
- Vectori de probabilitate
- Ce sunt spațiile de eșantionare?
- Modele stocastice.
- Ce este probabilitatea subiectivă?
- Ce este probabilitatea teoretică?
- Ce este un model de urnă?
Calculatoare.
- Calculator de permutări și calculator de combinații online.
Formule de probabilitate / Reguli de probabilitate
Unul dintre cele mai incomode lucruri care nu le plac studenților în legătură cu formulele este lipsa lor în probabilitate și statistică. Există câteva elemente de bază, inclusiv câteva notații pe care trebuie să le cunoașteți:
Intervalul de probabilitate
0 ≤ P(A) ≤ 1
Aceasta afirmă că probabilitatea unui eveniment este undeva între zero și 100% (ca zecimală, asta înseamnă 0 și 1). Veți dori să vă amintiți această regulă atunci când adăugați sau înmulțițiți probabilitățile unor evenimente. Dacă răspunsul tău este peste 100%, acesta este un indiciu că s-ar putea să fi făcut ceva greșit.
Regula evenimentelor complementare
P(AC) + P(A) = 1
Evenimentele complementare se întâmplă atunci când există doar două rezultate, cum ar fi aruncarea unei monede. Aruncarea unui zar pentru a vedea dacă veți obține șase este, de asemenea, complementară; singurele două rezultate sunt obținerea unui șase (o șansă de 1/6) sau neobținerea unui șase (o șansă de 5/6). Cele două probabilități trebuie să însumeze 1.
De asemenea, puteți vedea această formulă scrisă astfel:
p(A) + p(A’) = 1
care poate fi rearanjată algebric pentru a se citi:
p(A’) = 1 – p(A).
Toate cele trei formule sunt echivalente: ce terminologie (A’ sau Ac) este folosită depinde de autorul manualului și de profesor. Personal, prefer A’, pe care o numesc „nu A”. Probabilitatea de „nu A”, cred că este mai ușor de înțeles decât „complementul” (ori se întâmplă un eveniment, ori nu se întâmplă).
Regula adiției
P(A∪B) = P(A) + P(B) – P(A∩B)
unde ∪ este uniunea și ∩ este intersecția.
Ce spune aceasta (în engleză!) este că probabilitatea ca evenimentul A SAU evenimentul B să se întâmple (sau ambele în același timp) este:
- Probabilitatea ca evenimentul A să se întâmple de unul singur,
- Plus probabilitatea ca evenimentul B să se întâmple de unul singur,
- Plus probabilitatea ca ambele evenimente să se întâmple în același timp.
Dacă aveți evenimente care se exclud reciproc, atunci P(A∩B) nu se poate întâmpla (evenimentele nu se pot întâmpla împreună), deci formula devine: P(A∩B):
P(A∪B) = P(A)+P(B)- 0 = P(A)+P(B)
Evenimente disjuncte
Evenimentele A și B sunt disjuncte dacă:
P(A∩B) = 0
Acesta este doar un alt mod de a spune că evenimentele se exclud reciproc. Ele nu se pot întâmpla în același timp.
O formulă conexă este P((A∪B)c) sau, echivalent ((A∪B)’). În engleză, aceasta spune „nu uniunea”. Pentru a o rezolva, descifrați uniunea și îndepărtați rezultatul de 1 (deoarece probabilitatea ca evenimentele să se întâmple sau să nu se întâmple trebuie să însumeze 1).
Probabilitate condiționată
P(A|B) = P(A∩B) / P(B)
Simbolul „|” înseamnă „având în vedere că”. Cu alte cuvinte, probabilitatea ca evenimentul B să se întâmple, având în vedere că se întâmplă evenimentul A. Pentru exemple de utilizare a formulei, vezi: probabilitate condiționată.
Formula lui Bayes
P(A|B) = P(B|A) – P(A) / P(B)
Teorema lui Bayes este o modalitate de a calcula probabilitatea condiționată, deși este puțin mai nuanțată. Pe scurt, vă oferă probabilitatea reală a unui eveniment având în vedere informațiile despre teste. De exemplu, care este probabilitatea ca tu să ai cancer dacă testul medical este pozitiv (răspuns = mult mai mică decât crezi). Pentru câteva exemple, consultați: Exemple de Teoremă Bayes și Distribuții posterioare / Probabilități posterioare.
Evenimente independente
Evenimentele A și B sunt independente dacă unul dintre ele nu afectează probabilitatea celuilalt. De asemenea, se spune că evenimentele sunt independente dacă următoarea ecuație este adevărată.
P(A∩B) = P(A) – P(B).
Această ecuație este derivată din regula înmulțirii, care spune că P(A∩B) = P(A) * P(B|A). Deoarece știm că P(B|A) = P(B) pentru evenimente independente, putem înlocui P(B|A) cu P(B), ceea ce ne dă formula.
Câteva note despre regulile de probabilitate
Statistica se referă la șansă și la estimări, nu la absolut și la „răspunsul corect”. Este suficient să consultați orice sondaj Gallup – rareori sunt mai mult de 90% încrezători că au „răspunsul corect”. Există tehnici pe care le puteți folosi pentru a calcula șansele (cum ar fi înmulțirea a două probabilități sau adunarea lor). Cu toate acestea, în afară poate de tabelul de distribuție binomială și de formulele de mai sus (care, în viața reală, nu sunt folosite atât de mult), nu există cu adevărat nicio formulă de probabilitate pe care să o puteți aplica cu ușurință. Trebuie să vă întoarceți la vechea bază din școala primară, logica (o țineți minte… era acolo chiar înainte de a începe testele standardizate pentru a scoate logica din voi).
Cele trei reguli ale formulelor de probabilitate:
- Nu există reguli (ei bine, foarte puține, cu excepția celor enumerate mai sus).
- Utilizați logica, nu ecuațiile.
- Există multe, multe modalități diferite de a ajunge la răspuns – dintre care niciuna nu folosește cu adevărat formule.
Iată o întrebare care a sosit în inbox-ul meu în această dimineață și care abordează probabilitățile:
„Dacă ați încerca să colecționați 6 cartonașe de baseball care au venit în pachete de pufuleți cu brânză, presupunând că acestea sunt distribuite în mod egal, câte pachete de pufuleți cu brânză v-ați aștepta să cumpărați înainte de a avea toate cele 6 cartonașe?”
Pasul 1 pentru rezolvarea acestei probleme este să vă dați seama că nu puteți căuta răspunsul într-un tabel. Pentru a o rezolva, trebuie să gândiți ca un copil.
Cartea nr. 1: Aveți din nou 8 ani și intrați într-un magazin cu suficienți bani pentru a cumpăra o pungă de pufuleți cu brânză. Speri să colecționezi toate cele 5 cărți de baseball, dar încă nu ai niciuna. Care sunt șansele să cumperi o pungă și să primești o carte pe care ți-o dorești?
Răspunsul, bineînțeles, este 100%. Cumpărați prima pungă și aveți 100% șanse ca în ea să fie o carte pe care o doriți.
Cartea nr. 2: Acum devine un pic mai complicat. Vă întoarceți la magazin pentru a lua cartea#2. Dar cum ați luat deja cartea #1, Mickey Mantle. Nu îl vrei din nou, dar există o șansă de 1/5 să îl primești (și, prin urmare, o șansă de 4/5 să nu îl primești). Câte pungi de pufuleți cu brânză va trebui să cumperi pentru a obține cartea #2 devine o problemă de raport. Ți-ai putea da seama în minte, dar dacă vrei să o modelezi matematic trebuie să stabilești ecuația. Dacă o pungă de pufuleți cu brânză vă oferă 80% șanse de a obține cartea pe care o doriți, câte pungi trebuie să cumpărați pentru a obține o șansă de 100%?
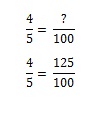
Pentru a obține 100% ar trebui să cumpărați 1,25 pungi.
Cartea nr. 3:Șansele încep să devină mai dificile. Aveți 60% șanse să obțineți a treia carte de baseball și va trebui să cumpărați 1,667 saci pentru a obține acea a treia carte.
Carte# 4:Șansele încep să devină puțin mai sumbre. Aveți 40% șanse să obțineți a patra carte de baseball, și va trebui să cumpărați 2,5 saci pentru a obține acea a treia carte.
Carte# 5:Șansele sunt împotriva dvs. Aveți 20% șanse să obțineți ultima carte și va trebui să cumpărați 5 saci pentru a obține acea a treia carte.
Atunci cantitatea totală de saci pe care va trebui să o cumpărați este egală cu:
1 + 1,25 + 1,667 + 2,5 + 5
Dar așteptați! (Și aici intervine un pic de logică). Nu poți intra într-un magazin și să cumperi 1,25 pungi de pufuleți cu brânză, așa că va trebui să rotunjești. Ecuația devine:
1 + 2 + 2 + 2 + 3 + 5 = 13 pungi.
Un punct important pentru formule: amintiți-vă că nimic nu este absolut. Sunt destul de încrezător că, dacă ați cumpărat 13 pungi de pufuleți cu brânză și presupunând că cărțile sunt distribuite în mod egal, veți primi toate cele 5 cărți. Dar… probabilitatea ține de șansă, și ar putea fi doar ghinionul tău să primești aceeași carte de 10 ori la rând (îmi amintesc că mi s-a întâmplat asta când eram copil). Dar ar putea exista și o altă explicație pentru „ghinionul” tău, și anume că firmele doresc să cumperi cât mai multe pungi, așa că vor încerca să facă șansele să lucreze în favoarea lor. Chiar dacă cărțile sunt distribuite în mod egal, compania ar putea trimite pungi cu cărțile nr. 1, nr. 2 și nr. 3 la un magazin (prin urmare, te-ar putea atrage, făcându-te să colectezi mai mult de jumătate din cărți), iar cărțile nr. 4 și nr. 5 la un alt magazin.
Ce alte moduri vă puteți gândi la care producătorii ar putea întoarce șansele în favoarea lor?
Probabilitatea ca un grup să aleagă același lucru
Întrebările de probabilitate pot fi împărțite în diferite tipuri. Atunci când vi se cere să găsiți probabilitatea ca un grup să aleagă același lucru, luați în considerare acțiunile unor membri aleatori ai unui grup (acesta poate fi la fel de mic ca un comitet sau poate fi la fel de mare ca populația SUA).
Aceste întrebări de probabilitate vă oferă un grup și vă cer să calculați probabilitatea ca un eveniment să aibă loc pentru un anumit număr de membri aleatori din acel grup.
Probabilitatea ca un grup să aleagă același lucru : Pași
Problemă de exemplu: Există 200 de persoane la un târg de carte. 159 dintre ele vor cumpăra cel puțin o carte. Dacă sondați 5 persoane la întâmplare care ies pe ușă, care este probabilitatea ca toate acestea să fi cumpărat cel puțin o carte?

Care este probabilitatea ca un grup să cumpere cel puțin o carte?
Etapa 1: Convertiți datele din întrebare într-o fracție. De exemplu, fraza „159 de persoane din 200” poate fi convertită în: 159/200.
Etapa 2: Înmulțițiți fracția cu ea însăși. Repetați pentru oricât de multe elemente aleatorii (adică persoane) sunt alese. În exemplul nostru, avem 5 persoane chestionate, așa că vrem:
159/200 x 159/200 x 159/200 x 159/200 x 159/200 x 159/200 x 159/200 = 0,3176
Așa se găsește probabilitatea ca un grup să aleagă același lucru!
Tip: Poate fi mai ușor să convertiți fracția în zecimală înainte de a o înmulți. În acest caz, 159/200 = 0,795.
Vezi canalul nostru YouTube pentru mai mult ajutor și sfaturi despre statistici! Avem videoclipuri pentru cele mai frecvente probleme pe care este posibil să le întâlniți. Plus videoclipuri pentru utilizarea Excel în statistici > totul, de la realizarea graficelor de bare de bază până la rezolvarea problemelor complexe de analiză a datelor.
Stephanie Glen. „Introducere în probabilitate: Articole și videoclipuri cu soluții!” De pe StatisticsHowTo.com: Statistică elementară pentru noi toți ceilalți! https://www.statisticshowto.com/probability-and-statistics/probability-main-index/
——————————————————————————
Nevoie de ajutor cu o temă pentru acasă sau o întrebare de test? Cu Chegg Study, puteți obține soluții pas cu pas la întrebările dvs. de la un expert în domeniu. Primele 30 de minute cu un tutore Chegg sunt gratuite!




