Proprietăți ale cvadrilateralelor – dreptunghi, pătrat, paralelogram, romb, trapez

Proprietăți ale cvadrilateralelor – dreptunghi, pătrat, paralelogram, romb, trapez

În geometria euclidiană, un cvadrilater este o figură cu patru laturi 2D a cărei sumă a unghiurilor interne este de 360°. Cuvântul cvadrilaterală derivă din două cuvinte latinești „quadri” și „latus” care înseamnă patru și, respectiv, latură. Prin urmare, identificarea proprietăților cvadrilateralelor este importantă atunci când încercăm să le distingem de alte poligoane.

Atunci, care sunt proprietățile cvadrilateralelor? Există două proprietăți ale cvadrilateralelor:

• Un cvadrilater ar trebui să fie o formă închisă cu 4 laturi
• Toate unghiurile interne ale unui cvadrilater se însumează la 360°

În acest articol, vă veți face o idee despre cele 5 tipuri de cvadrilaterale și veți afla despre proprietățile cvadrilateralelor.

Acesta este ceea ce veți citi în articol:

• Diferite tipuri de cuadrilatere
• Dreptunghi
  • Proprietăți ale dreptunghiurilor
  • Formulele dreptunghiurilor
• Pătrat
  • Proprietăți unui pătrat
  • Formule de pătrate
• Paralelogram
  • Proprietăți ale paralelogramelor
  • Formule de paralelogram
• . Romb
  • Proprietățile unui romb
  • Formulele rombului
• Trapez/Trapezoid
  • Proprietățile unui trapez
  • Formulele trapezului

.

Proprietățile cvadrilaterilor

Formule importante ale cvadrilaterilor

Întrebări despre cvadrilaterale

Iată un video care explică proprietățile cvadrilaterilor:

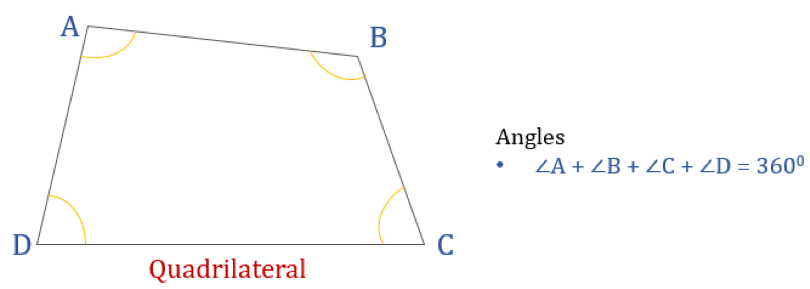
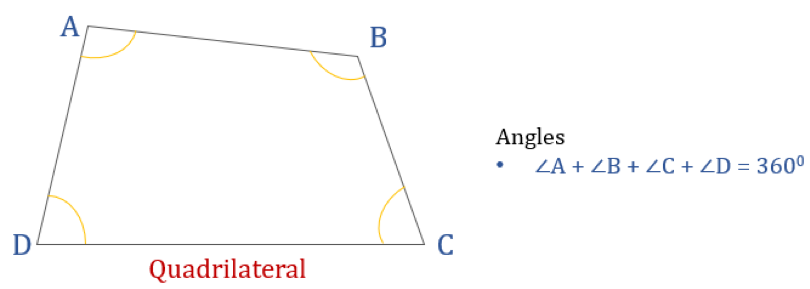
Diagrama dată mai jos prezintă un cuadrilater ABCD și suma unghiurilor sale interne. Toate unghiurile interne însumează 360°.

Așa, ∠A + ∠B + ∠C + ∠D = 360°

Diferite tipuri de cuadrilatere

Există 5 tipuri de cuadrilatere în funcție de forma lor. Aceste 5 cvadrilaterale sunt:

1. Rectunghiul
2. Pătrat
3. Paralelogramul
4. Rhombus
5. Trapezul

Să discutăm în detaliu fiecare dintre aceste 5 cvadrilaterale:

Iată întrebări care vă vor învăța cum să aplicați proprietățile tuturor celor 5 cuadrilatere pe care le veți învăța în acest articol.

Rectunghiul

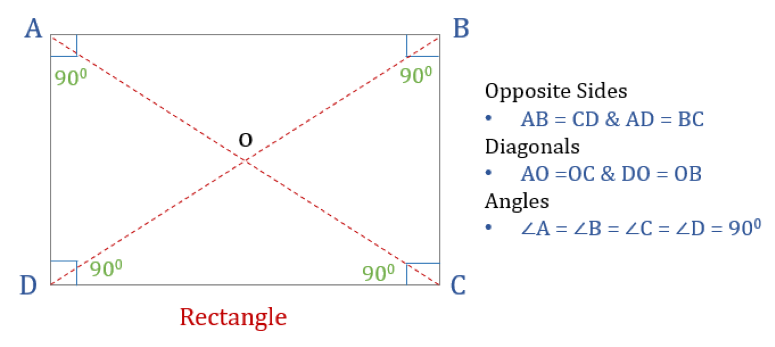
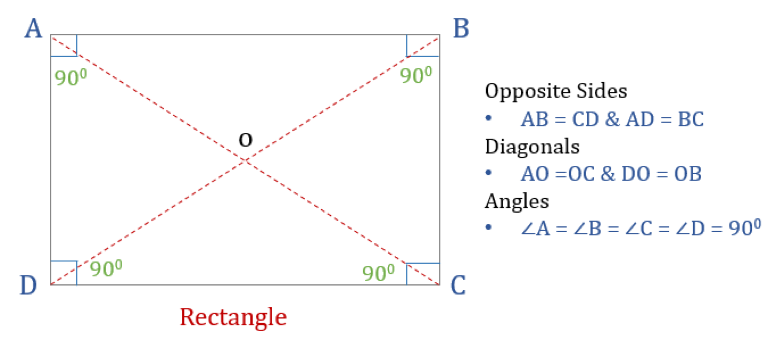
Un dreptunghi este un cuadrilater cu patru unghiuri drepte. Astfel, toate unghiurile dintr-un dreptunghi sunt egale (360°/4 = 90°). Mai mult decât atât, laturile opuse ale unui dreptunghi sunt paralele și egale, iar diagonalele se bisectează între ele.

Proprietăți ale dreptunghiurilor

Un dreptunghi are trei proprietăți:

• Toate unghiurile unui dreptunghi sunt de 90°
• Legimile opuse ale unui dreptunghi sunt egale și paralele
• Diagonalele unui dreptunghi se bisectează între ele

Formula dreptunghiului – Aria și perimetrul unui dreptunghi

Dacă lungimea dreptunghiului este L și lățimea este B atunci,

1. Aria unui dreptunghi = Lungime × lățime sau L × B
2. Perimetrul dreptunghiului = 2 × (L + B)

Aceste întrebări practice vă vor ajuta să consolidați proprietățile dreptunghiurilor

Pătrat

Pătratul este un cvadrilater cu patru laturi și unghiuri egale. Este, de asemenea, un cvadrilateral regulat, deoarece atât laturile cât și unghiurile sale sunt egale. La fel ca un dreptunghi, un pătrat are patru unghiuri de 90° fiecare. De asemenea, poate fi văzut ca un dreptunghi ale cărui două laturi adiacente sunt egale.

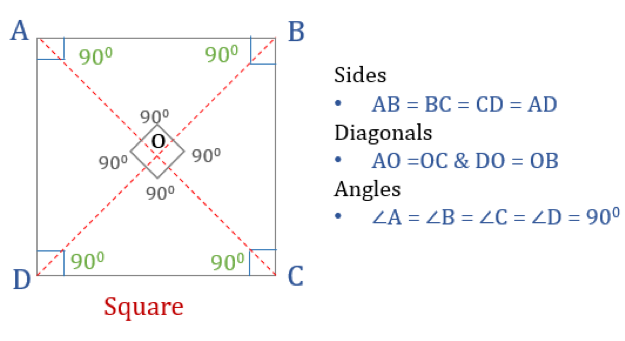
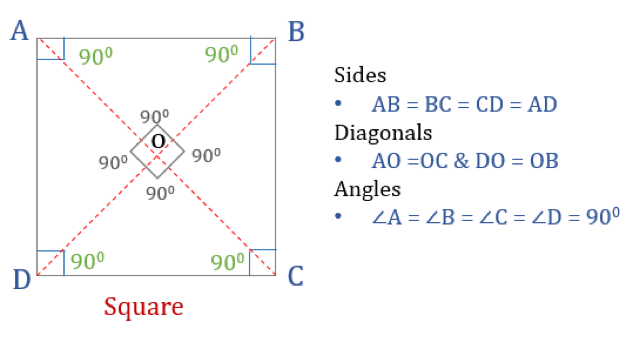
Proprietăți ale unui pătrat

Pentru ca un cuadrilater să fie un pătrat, el trebuie să aibă anumite proprietăți. Iată cele trei proprietăți ale pătratelor:

• Toate unghiurile unui pătrat sunt de 90°
• Toate laturile unui pătrat sunt egale și paralele între ele
• Diagonalele se taie în două perpendicular

Formula pătratului – Aria și perimetrul unui pătrat

Dacă latura unui pătrat este „a” atunci,

1. Aria pătratului = a × a = a²
2. Perimetrul pătratului = 2 × (a + a) = 4a

Aceste întrebări practice vă vor ajuta să solidificați proprietățile pătratelor

Scoaterea unui Q50-51 la GMAT vă ajută să obțineți un scor GMAT de 700+. De ce nu începi să te pregătești pentru GMAT cu resursele noastre gratuite de pregătire și să începi călătoria ta pentru a obține un Q50-51 la GMAT. Învățați de la Carrie Law, care s-a îmbunătățit de la Q35 la Q50 în 3 săptămâni.

Paralelogramă

Un paralelogram, după cum sugerează și numele, este un cuadrilater simplu ale cărui laturi opuse sunt paralele. Astfel, el are două perechi de laturi paralele. Mai mult, unghiurile opuse într-un paralelogram sunt egale, iar diagonalele sale se bisectează între ele.

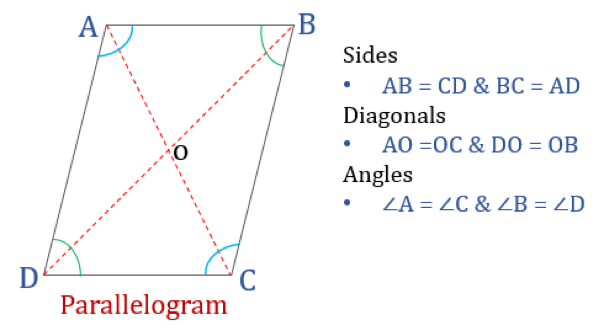
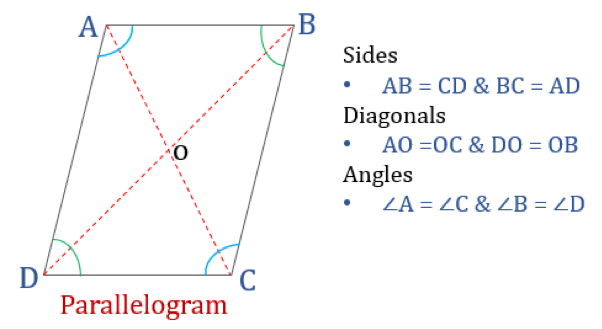
Proprietăți ale paralelogramului

Un cuadrilater care satisface proprietățile menționate mai jos va fi clasificat ca paralelogram. Un paralelogram are patru proprietăți:

• Unghiurile opuse sunt egale
• Legumele opuse sunt egale și paralele
• Diagonalele se bisectează
• Suma oricăror două unghiuri adiacente este 180°

Formulele paralelogramelor – Aria și perimetrul unui paralelogram

Dacă lungimea unui paralelogram este „l”, lățimea este „b” și înălțimea este „h”, atunci:

1. Perimetrul paralelogramului= 2 × (l + b)
2. Aria paralelogramului = l × h

Aceste întrebări practice vă vor ajuta să vă solidificați proprietățile paralelogramului

Rombul

Un romb este un cuadrilater ale cărui toate cele patru laturi au lungimi egale și laturile opuse sunt paralele între ele. Cu toate acestea, unghiurile nu sunt egale cu 90°. Un romb cu unghiuri drepte ar deveni un pătrat. Un alt nume pentru romb este „romb”, deoarece arată asemănător cu rombul din cărțile de joc.

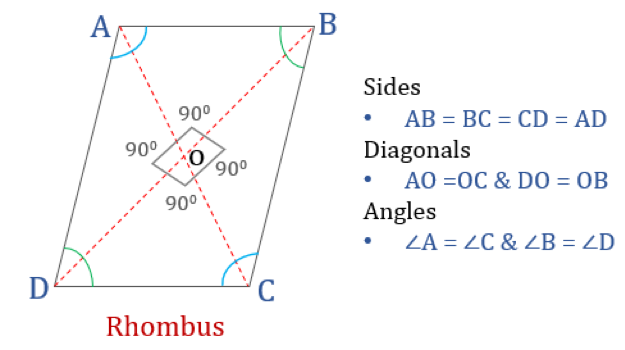
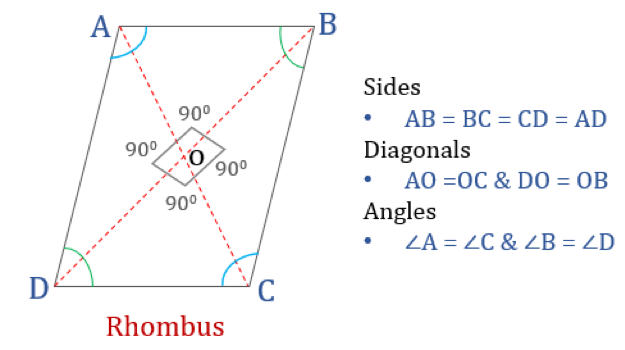
Proprietăți ale rombului

Un romb este un cuadrilater care are următoarele patru proprietăți:

• Unghiurile opuse sunt egale
• Toate laturile sunt egale și, laturile opuse sunt paralele între ele
• Diagonalele se bisectează între ele perpendicular
• Suma oricăror două unghiuri adiacente este 180°

Formulele rombului – Aria și perimetrul unui romb

Dacă latura unui romb este a atunci, perimetrul unui romb = 4a

Dacă lungimea a două diagonale ale rombului este d1 și d2 atunci aria unui romb = ½ × d1 × d2

Aceste întrebări practice vor vă vor ajuta să consolidați proprietățile rombului

Trapezul

Un trapez (numit trapez în SUA) este un cuadrilater care are doar o pereche de laturi paralele. Laturile paralele sunt denumite „baze”, iar celelalte două laturi se numesc „picioare” sau laturi laterale.

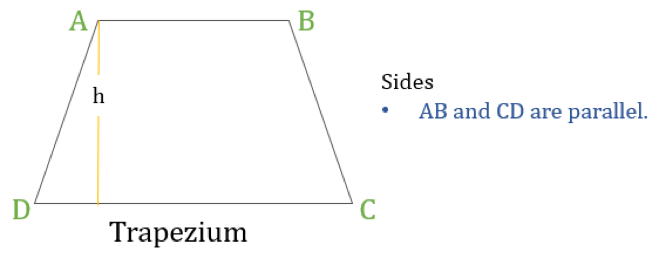
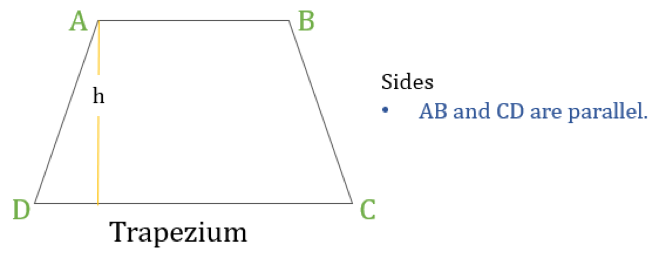
Proprietăți ale trapezului

Un trapez este un cvadrilater în care una dintre următoarele proprietăți este următoarea:

• Doar o pereche de laturi opuse sunt paralele între ele

Formulele trapezului – Aria și perimetrul unui trapez

Dacă înălțimea unui trapez este „h” (așa cum se arată în diagrama de mai sus) atunci:

1. Perimetrul trapezului= Suma lungimilor tuturor laturilor = AB + BC + CD + DA
2. Aria trapezului = ½ × (Suma lungimilor laturilor paralele) × h = ½ × (AB + CD) × h

Aceste întrebări practice vă vor ajuta să consolidați proprietățile trapezului

Proprietăți ale cuadrilaterilor

Tabelul de mai jos rezumă toate proprietățile cuadrilaterilor pe care le-am învățat până acum:

.

.

.

.

.

Proprietățile cuadrilaterilor	Rectunghiul	Cadrul	Pătrat	Paralelogramul	Rombul	Trapezul
Toate laturile sunt egale	✖	✔	✖	✔	✖	✖
Opusă Părțile sunt egale	✔	✔	✔	✔	✖
Opuse Părțile sunt paralele	✔	✔	✔	✔	✔
Toate unghiurile sunt egale	✔	✔	✔	✖	✖	✖
Unghiurile opuse sunt egale	✔	✔	✔	✔	✔	✖
Suma a două unghiuri adiacente este 180	✔	✔	✔	✔	✔	✖
Bisectează unul de altul	✔	✔	✔	✔	✖
Bisectează perpendicular	✖	✔	✖	✔	✖

Imaginea de mai jos rezumă, de asemenea, proprietățile cuadrilaterilor:

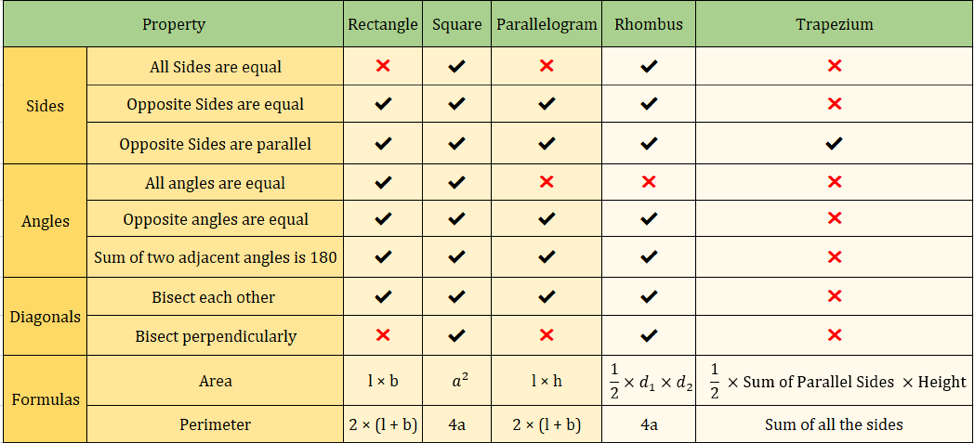
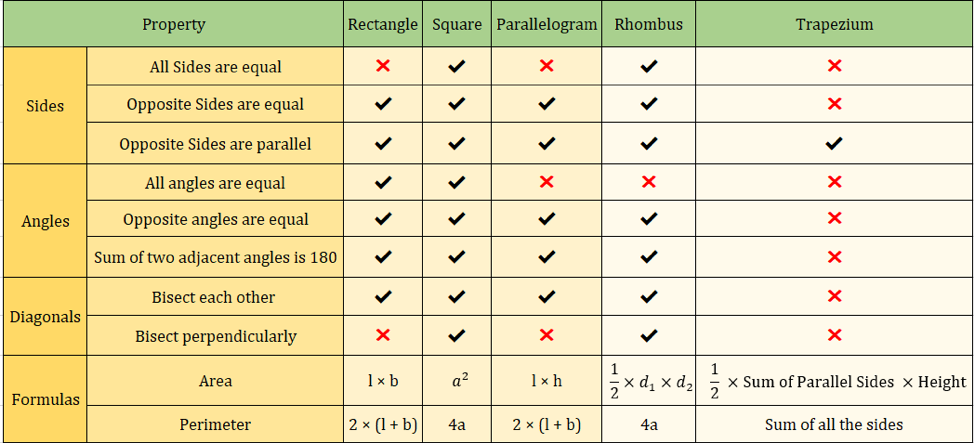
Formule importante ale cuadrilateralelor

Tabelul de mai jos rezumă formulele privind aria și perimetrul diferitelor tipuri de cuadrilatere:

.

.

Formulele cvadrilateralelor	Rectunghiul	Cadrul	Paralelogramul	Rhombus	Trapezul
Arie	l × b	a²	l × h	½ × d1 × d2	½ × (Suma laturilor paralele) × înălțime
Perimetru	2 × (l + b)	4a	2 × (l + b)	4a	Suma tuturor laturilor

Citește mai departe:

• Proprietăți ale cercului | Formulele cercului – Aria și perimetrul
• Proprietăți ale numerelor – Pere & Impar | Prime | HCF & LCM
• Proprietăți ale triunghiurilor – Definiție | Tipuri | Clasificare
• Liniile și unghiurile – Proprietăți și aplicarea lor

Întrebări despre cvadrilatere

Să exersăm aplicarea proprietăților cvadrilaterilor la următoarele exemple de întrebări:

Întrebare 1

Adam vrea să construiască un gard în jurul grădinii sale dreptunghiulare cu lungimea de 10 metri și lățimea de 15 metri. Câți metri de gard ar trebui să cumpere pentru a împrejmui toată grădina?

1. 20 de metri
2. 25 de metri
3. 30 de metri
4. 40 de metri
5. 50 de metri

Soluția

Etapa 1: Având în vedere

• Adam are o grădină dreptunghiulară.
  • Ea are o lungime de 10 metri și o lățime de 15 metri.
  • El vrea să construiască un gard în jurul ei.

Etapa 2: Să se afle

• Lungimea necesară pentru a construi gardul în jurul întregii grădini.

Etapa 3: Abordarea și calculul

Gardul poate fi construit numai în jurul laturilor exterioare ale grădinii.

• Deci, lungimea totală a gardului necesar= Suma lungimilor tuturor laturilor grădinii.
  • Din moment ce grădina este dreptunghiulară, suma lungimilor tuturor laturilor nu este altceva decât perimetrul grădinii.
  • Perimetrul = 2 × (10 + 15) = 50 metri

În consecință, lungimea necesară a gardului este de 50 de metri.

În consecință, opțiunea E este răspunsul corect.

Întrebare: 2

Steve vrea să vopsească un perete de formă dreptunghiulară al camerei sale. Costul pentru vopsirea peretelui este de 1,5 dolari pe metru pătrat. Dacă peretele are o lungime de 25 de metri și o lățime de 18 metri, atunci care este costul total de vopsire a peretelui?

1. $ 300
2. $ 350
3. $ 450
4. $ 600
5. $ 675

Soluție

Pasul 1: Dat fiind

• Steve vrea să vopsească un perete al camerei sale.
  • Peretele are 25 de metri lungime și 18 metri lățime.
  • Costul de vopsire a peretelui este de 1,5 dolari pe metru pătrat.

Etapa 2: Să aflăm

• Costul total de vopsire a peretelui.

Etapa 3: Abordarea și calculul

• Un perete este vopsit pe toată suprafața sa.
  • Atunci, dacă găsim suprafața totală a peretelui în metri pătrați și o înmulțim cu costul de vopsire a 1 metru pătrat de perete, atunci putem obține costul total.
  • Suprafața peretelui = lungime × lățime = 25 metri × 18 metri = 450 de metri pătrați
  • Costul total de vopsire a peretelui = 450 × 1 $.5 = 675 $

În consecință, răspunsul corect este opțiunea E.

Sperăm că până acum ați învățat diferitele tipuri de cuadrilatere, proprietățile și formulele lor și cum să aplicați aceste concepte pentru a rezolva întrebări despre cuadrilatere. Aplicarea cuadrilateralelor este importantă pentru a rezolva întrebările de geometrie din cadrul GMAT. Dacă intenționați să dați testul GMAT, vă putem ajuta cu materiale de studiu de înaltă calitate, pe care le puteți accesa gratuit înregistrându-vă aici.

Iată alte câteva articole despre matematică:

1. Îmbunătățiți acuratețea la întrebările de matematică despre poligoane
2. Întrebări de geometrie – Cele mai frecvente greșeli | GMAT Quant Prep

Dacă plănuiți să dați GMAT, vă putem oferi acces la conținut online de calitate pentru a vă pregăti. Suntem cea mai recenzată companie de pregătire GMAT de pe gmatclub, cu peste 1950 de recenzii.

De ce nu faceți o încercare gratuită și judecați singuri?

Scrieți-ne la [email protected] în cazul oricărei întrebări.

.