Skewness – Introducere rapidă, exemple și formule
Skewness este un număr care indică în ce măsură
o variabilă este distribuită asimetric.
- Exemplu de skewness pozitiv (dreapta)
- Exemplu de skewness negativ (stânga)
- Exemplu de skewness negativ (stânga)
- Skewness de populație – formulă și calcul
- Skewness de eșantionare – Formula și calculul
- Skewness în SPSS
- Skewness – Implicații pentru analiza datelor
Skewness pozitiv (dreapta) Exemplu
Un om de știință are 1,000 de persoane să completeze niște teste psihologice. Pentru testul 5, scorurile testului au skewness = 2,0. O histogramă a acestor scoruri este prezentată mai jos.
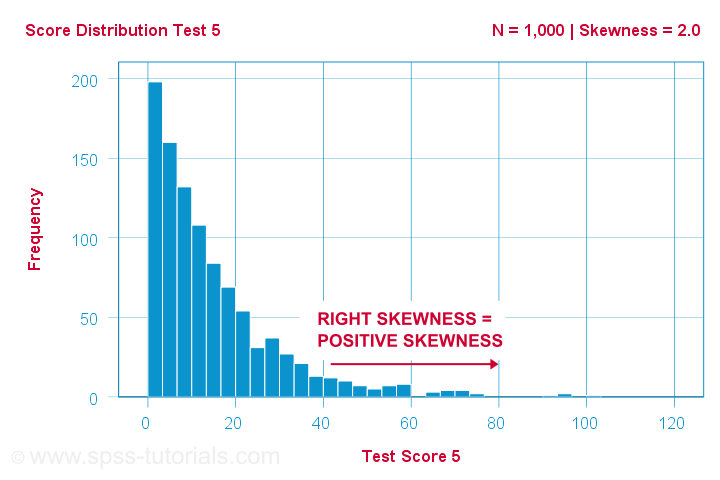
Histograma arată o distribuție de frecvență foarte asimetrică. Cei mai mulți oameni obțin scoruri de 20 de puncte sau mai mici, dar coada din dreapta se întinde până la 90 sau cam așa ceva. Această distribuție este înclinată spre dreapta.
Dacă ne deplasăm spre dreapta de-a lungul axei x, trecem de la 0 la 20 la 40 de puncte și așa mai departe. Așadar, spre dreapta graficului, scorurile devin mai pozitive. Prin urmare, asimetria spre dreapta este o asimetrie pozitivă, ceea ce înseamnă că asimetria > 0. Acest prim exemplu are asimetria = 2,0, așa cum este indicat în colțul din dreapta sus al graficului. Scorurile sunt puternic asimetrice pozitiv.
Exemplu de asimetrie negativă (stânga)
O altă variabilă – scorurile la testul 2- se dovedește a avea asimetria = -1,0. Histograma lor este prezentată mai jos.

Cei mai mulți scoruri sunt între 60 și 100 sau cam așa ceva. Cu toate acestea, coada din stânga este oarecum întinsă. Deci, această distribuție este asimetrică spre stânga.
Dreapta: spre stânga, spre stânga. Dacă urmărim axa x spre stânga, ne îndreptăm spre scoruri mai negative. Acesta este motivul pentru care asimetria spre stânga este asimetria negativă. și, într-adevăr, asimetria = -1,0 pentru aceste scoruri. Distribuția lor este înclinată spre stânga. Cu toate acestea, este mai puțin înclinată – sau mai simetrică – decât primul nostru exemplu care avea skewness = 2.0.
Distribuția simetrică implică skewness zero
În cele din urmă, distribuțiile simetrice au skewness = 0. Scorurile de la testul 3 -care au skewness = 0.1- se apropie.

Acum, distribuțiile observate sunt rareori exact simetrice. Acest lucru se observă mai ales în cazul unor distribuții teoretice de eșantionare. Câteva exemple sunt
- distribuția normală (standard);
- distribuția t și
- distribuția binomială dacă p = 0,5.
Aceste distribuții sunt toate exact simetrice și astfel au skewness = 0.000…
Skewnessul unei populații – formulă și calcul
Dacă doriți să calculați skewnessurile pentru una sau mai multe variabile, lăsați calculele în seama unui soft. Dar -doar de dragul completării- voi enumera totuși formulele.
Dacă datele dvs. conțin întreaga populație, calculați skewness-ul populației ca:
$$Populația\;skewness = \Sigma\biggl(\frac{X_i – \mu}{\sigma}\biggr)^3\cdot\frac{1}{N}$$$
unde
- \(X_i\) este fiecare scor individual;
- \(\mu\) este media populației;
- \(\sigma\) este abaterea standard a populației și
- \(N\) este mărimea populației.
Pentru un exemplu de calcul folosind această formulă, consultați această foaie Googlesheet (prezentată mai jos).
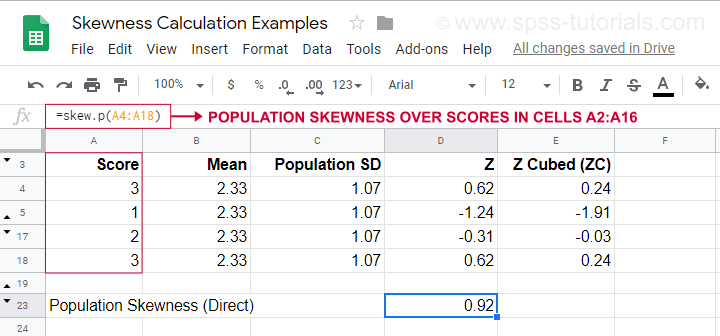
Ea arată, de asemenea, cum se poate obține direct asimetria populației folosind=SKEW.P(…)unde „.P” înseamnă „populație”. Acest lucru confirmă rezultatul calculului nostru manual. Din păcate, nici SPSS, nici JASP nu calculează skewness-ul populației: ambele sunt limitate la skewness-ul eșantionului.
Skewness de eșantion – Formulă și calcul
Dacă datele dvs. dețin un eșantion aleatoriu simplu dintr-o anumită populație, utilizați
$$$Sample\;skewness = \frac{N\cdot\Sigma(X_i – \supralinie{X})^3}{S^3(N – 1)(N – 2)}$$
unde
- \(X_i\) este fiecare scor individual;
- \(\sobrelinie{X}\) este media eșantionului;
- \(S\) este deviația standard a eșantionului și
- \(N\) este dimensiunea eșantionului.
Un exemplu de calcul este prezentat în această foaie Googlesheet (prezentată mai jos).
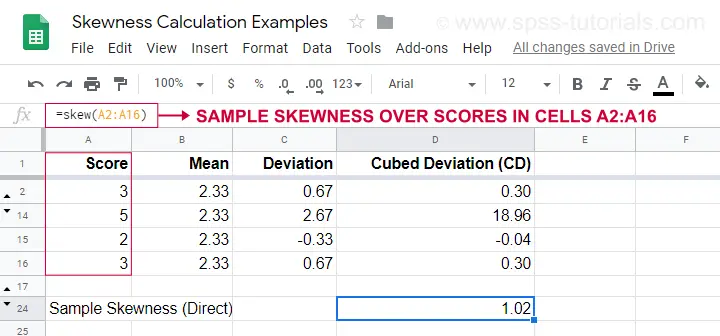
O opțiune mai ușoară pentru obținerea asimetriei eșantionului este utilizarea=SKEW(…).care confirmă rezultatul calculului nostru manual.
Skewness în SPSS
În primul rând, „skewness” în SPSS se referă întotdeauna la skewness de eșantion: se presupune în liniște că datele dvs. dețin un eșantion și nu o întreagă populație. Există o mulțime de opțiuni pentru a o obține. Preferata mea este prin MEANS, deoarece sintaxa și rezultatul sunt simple și clare. Capturile de ecran de mai jos vă ghidează.


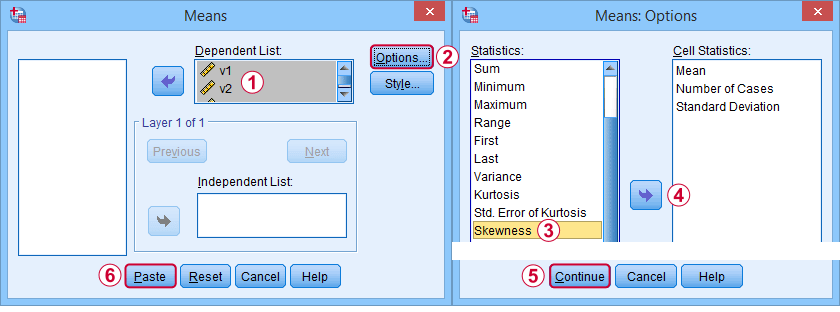
Sintaxa poate fi la fel de simplă cameans v1 to v5
/cells skew. un tabel foarte complet -incluzând mediile, abaterile standard, medianele și multe altele- este rulat de lameans v1 to v5
/cells count min max mean max median median stddev skew kurt.Rezultatul este prezentat mai jos.
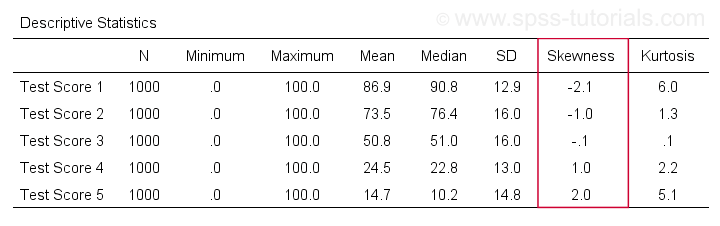
Skewness – Implicații pentru analiza datelor
Multe analize -ANOVA, teste t, regresie și altele- necesită ipoteza normalității: variabilele trebuie să fie distribuite normal în populație. Distribuția normală are skewness = 0. Deci, observarea unei skewness substanțiale în unele date din eșantion sugerează că ipoteza normalității este încălcată.
Aceste încălcări ale normalității nu reprezintă o problemă pentru eșantioane de dimensiuni mari -să spunem N > 20 sau 25 sau cam așa ceva. În acest caz, majoritatea testelor sunt robuste la astfel de încălcări. Acest lucru se datorează teoremei limitei centrale. Pe scurt,pentru dimensiuni mari ale eșantioanelor, asimetria nu este
o problemă reală pentru testele statistice. cu toate acestea, asimetria este adesea asociată cu deviații standard mari. Acestea pot avea ca rezultat erori standard mari și putere statistică scăzută. La fel, o asimetrie substanțială poate scădea șansele de respingere a unor ipoteze nule pentru a demonstra un anumit efect. În acest caz, un test neparametric poate fi o alegere mai înțeleaptă, deoarece poate avea mai multă putere. încălcările normalității reprezintă o amenințare reală
pentru eșantioane mici de -să spunem- N < 20 sau cam așa ceva. În cazul eșantioanelor de dimensiuni mici, multe teste nu sunt robuste la o încălcare a ipotezei normalității. Soluția -încă o dată- este utilizarea unui test neparametric, deoarece acestea nu necesită normalitate.
În sfârșit, dar nu în ultimul rând, nu există niciun test statistic pentru a examina dacă asimetria populației = 0. O modalitate indirectă de a testa acest lucru este un test de normalitate, cum ar fi
- testul de normalitate Kolmogorov-Smirnov și
- testul de normalitate Shapiro-Wilk.
Cu toate acestea, atunci când normalitatea este cu adevărat necesară -cu eșantioane de dimensiuni mici- astfel de teste au o putere scăzută: este posibil să nu atingă semnificația statistică chiar și atunci când abaterile de la normalitate sunt severe. Ca atare, ele vă oferă, în principal, un fals sentiment de siguranță.
.




